Естественная параметризация кривой

К лекции №5 от 05.03.14.

Длина дуги кривой

Рассмотрим кривую γ заданную = (х (t); y (t); z (t)) t (a, b).

Интервал (a, b) разобьем на n частей точками t ₀= a, t ₁,…, t_п = b. Получим точки на кривой М₀, М₁, …, М _п. Рассмотрим i -ый кусок Δ t_i = t_i+1 - t_i.

, - = Δ

Следовательно =

Рассмотрим сумму длин всех хорд и длин соответствующих отрезков по касательной .

Пусть последовательность разбиений такая, что тах Δ t_i → 0.

= →

Так как │ │ является некоторой скалярной функцией f (t)

= = =

Таким образом, длина ломанной, вписанной в кривую, при бесконечном измельчении стремится к пределу, который называется длиной кривой.

l_γ = (*)

Т.к.

l_γ =

Частные случаи для плоских кривых γ:

1. γ задана явным уравнением у = f (х) l_γ = .

2. γ задана в полярной системе координат: ,

в качестве параметра t = φ (α, β).

,

l_γ = .

Естественная параметризация кривой

Выбор параметра t на кривой произволен. Выберем параметризацию непосредственно связанную с самой кривой, а именно в качестве параметра возьмем длину дуги кривой.

Пусть γ: = (х (t); y (t); z (t)) t (a, b), фиксируем некоторую точку М₀(t ₀) в качестве начала отсчета, тогда М (t) γ ММ₀ =

В формуле (*) подразумевалось, что a < b, a у нас может быть t ₀ < t или t < t ₀ значит, величина S = может быть и положительной и отрицательной и зависит от t. Т.е. - функция (интеграл с переменным верхним пределом).

s ′(t) = │ │ > 0 s (t) - монотонно возрастающая функция, а значит для нее существует обратная, т.е. существует функция t = t (s). (Почему?)

Т.о. любой точке кривой соответствует некоторое значение s. И, наоборот, любому значению s (из некоторого интервала) соответствует единственная точка на кривой. Т.е. в качестве параметра действительно можно взять s – длину дуги кривой. Произвол остается только в выборе начала отсчета и направления отсчета.

Определение: Если в качестве параметра выступает длина дуги кривой, то такая параметризация называется естественной или натуральной параметризацией кривой.

Замечание: В некоторых случаях переход к естественному параметру s неудобен из-за громоздких вычислений.

Вернемся к s ′(t) = │ │ .

Т.е. модуль дифференциала длины дуги равен модулю дифференциала радиус-вектора.

Обозначение: В дальнейшем будем обозначать производную по естественному параметру - и производную по произвольному параметру .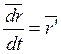

Вернемся к , отсюда можно получить несколько полезных формул:

(1) = = 1 (2) t ′(s)=

Формулу (1) иногда называют основным свойством естественного параметра – модуль производной по естественному параметру равен 1.

Рассмотрим еще несколько формул.

Т.е. векторы ↑↑ и отличаются только длиной. Вектор имеет единичную длину, а длина вектора не равна 1. Вектор является направляющим вектором касательной, а значит, будет единичным направляющим вектором касательной, т.е. = .

Т.к. вектор имеет постоянную длину равную 1, то по свойству вектор-функции или .

Рассмотрим

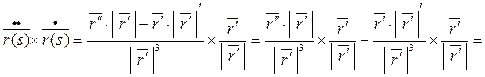
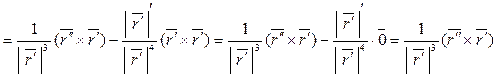
Т.е. , но т.к. и

Тогда - коллинеарен направляющему вектору главной нормали (т.к. касательная, бинормаль и главная нормаль попарно перпендикулярны).

Условимся единичный вектор главной нормали откладывать в направлении вектора , т.е. .

Единичный вектор бинормали направим так, чтобы тройка векторов была правой, т.е. .

Не нашли, что искали? Воспользуйтесь поиском: