
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Сопровождающий трехгранник кривой
Лекция № 5 от 05.03.14.
Пусть в окрестности точки М дана регулярная кривая заданная вектор-функцией  . Значит для нее можно найти уравнения касательной, нормальной и соприкасающейся плоскостей, причем эти плоскости будут взаимно перпендикулярны и любая прямая лежащая в нормальной плоскости будет перпендикулярна касательной. Среди этих прямых (нормалей) выберем две: одну перпендикулярную соприкасающейся плоскости, другую лежащую на соприкасающейся плоскости.
. Значит для нее можно найти уравнения касательной, нормальной и соприкасающейся плоскостей, причем эти плоскости будут взаимно перпендикулярны и любая прямая лежащая в нормальной плоскости будет перпендикулярна касательной. Среди этих прямых (нормалей) выберем две: одну перпендикулярную соприкасающейся плоскости, другую лежащую на соприкасающейся плоскости.
Определение: Нормаль, перпендикулярная соприкасающейся плоскости называется бинормалью.
Направляющий вектор бинормали можно найти, используя нормальный вектор соприкасающейся плоскости -  ×
×  ||
|| 
Определение: Нормаль, лежащая на соприкасающейся плоскости, называется главной нормалью.
Замечание: Бинормаль и главная нормаль перпендикулярны друг другу.
Т.о. имеется три взаимно перпендикулярных прямых – касательная, бинормаль и главная нормаль. Т.е. в окрестности точки М образовалась ПДСК, связанная с кривой, координатные оси которой совпадают с этими прямыми. Двумя координатными плоскостями являются нормальная и соприкасающаяся плоскости. К ним можно добавить третью плоскость, проходящую через касательную и бинормаль.
Определение: Плоскость, содержащую бинормаль и касательную будем называть спрямляющей.
Тогда вектор перпендикулярный спрямляющей плоскости, можно найти с помощью векторного произведения направляющего вектора касательной и направляющего вектора бинормали -  ||
||  ×(
×( ×
×  ). А так как главная нормаль перпендикулярна спрямляющей плоскости, то этот же вектор
). А так как главная нормаль перпендикулярна спрямляющей плоскости, то этот же вектор  можно считать направляющим вектором главной нормали.
можно считать направляющим вектором главной нормали.
РИСУНОК

Вывод: В окрестности точки кривой существует система, состоящая из трех взаимно перпендикулярных прямых (касательной, бинормали и главной нормали) и трех взаимно перпендикулярных плоскостей (нормальной, соприкасающейся и спрямляющей).
Определение: Совокупность трех прямых (касательной, бинормали и главной нормали) и трех взаимно перпендикулярных плоскостей (нормальной, соприкасающейся и спрямляющей) называется сопровождающим трехгранником кривой.
| прямые | параллельный (направляющий) | векторы | нормальный (перпендикулярный) | плоскости |
| касательная |  = = 
| нормальная | ||
| бинормаль |  = =  × × 
| соприкасающаяся | ||
| главная нормаль |  = =  ×( ×( × ×  ) )
| спрямляющая |
Задача. Составить уравнения сопровождающего трехгранника кривой γ:  в точке М для которой t = 4.
в точке М для которой t = 4.
Решение. Найдем координаты точки М и векторы первой и второй производных.

 М(6; -3; 0)
М(6; -3; 0)
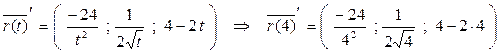 =(-1,5; 0,25;-4).
=(-1,5; 0,25;-4).
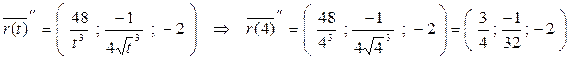
Тогда  ||
||  ||(-1,5; 0,25;-4)||(6; -1; 16).
||(-1,5; 0,25;-4)||(6; -1; 16).
 ║
║  ×
× 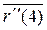 =
=  || (40; 384; 9)
|| (40; 384; 9)
 ║
║  ×(
×( ×
× 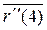 )=
)= 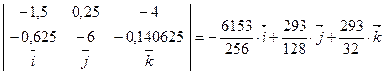
 || (-6153; 586; 2344)
|| (-6153; 586; 2344)
Тогда уравнения сопровождающего трехгранника кривой в точке М имеют вид:
Касательная - 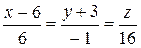
Нормальная плоскость - 6 х – у +16 z – 39 = 0
Бинормаль - 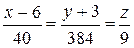
Соприкасающаяся плоскость - 40 х + 384 у + 9 z + 912 = 0
Главная нормаль - 
Спрямляющая плоскость - -6153 х + 586 у +2344 z – 35160 = 0
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Классификация семьи по:составу,распределению власти,месту проживания и другие. |
Не нашли, что искали? Воспользуйтесь поиском: