
Главная
Популярная публикация
Научная публикация
Случайная публикация
Обратная связь
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Ценовые и неценовые факторы
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
|
Задание В6. Классическое определение вероятности
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати
| Тип
| Условие
| | B6
| B 6 № 1001. На экзамен вынесено 60 вопросов, Андрей не выучил 3 из них. Найдите вероятность того, что ему попадется выученный вопрос.
Решение.
Андрей выучил 60 – 3 = 57 вопросов. Поэтому вероятность того, что на экзамене ему попадется выученный вопрос равна
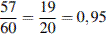 .
Ответ: 0,95. .
Ответ: 0,95.
| | | Тип
| Условие
| | B6
| B 6 № 1011. В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси.
Решение.
Вероятность того, что к заказчице приедет зеленое такси равна
 .
Ответ: 0,4. .
Ответ: 0,4.
| | | Тип
| Условие
| | B6
| B 6 № 1024. На тарелке 16 пирожков: 7 с рыбой, 5 с вареньем и 4 с вишней. Юля наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
Решение.
вероятность того, что пирожок окажется с вишней равна
 .
Ответ: 0,25. .
Ответ: 0,25.
| | | Тип
| Условие
| | B6
| B 6 № 282853. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Решение.
Количество исходов, при которых в результате броска игральных костей выпадет 8 очков, равно 5: 2+6, 3+5, 4+4, 5+3, 6+2. Каждый из кубиков может выпасть шестью вариантами, поэтому общее число исходов равно 6·6 = 36. Следовательно, вероятность того, что в сумме выпадет 8 очков, равна
 Ответ: 0,14.
Ответ: 0,14.
| | | Тип
| Условие
| | B6
| B 6 № 282854. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
Решение.
Равновозможны 4 исхода эксперимента: орел-орел, орел-решка, решка-орел, решка-решка. Орел выпадает ровно один раз в двух случаях: орел-решка и решка-орел. Поэтому вероятность того, что орел выпадет ровно 1 раз, равна
 .
Ответ: 0,5. .
Ответ: 0,5.
| | | Тип
| Условие
| | B6
| B 6 № 282855. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Решение.
В чемпионате принимает участие  спортсменок из Китая. Тогда вероятность того, что спортсменка, выступающая первой, окажется из Китая, равна спортсменок из Китая. Тогда вероятность того, что спортсменка, выступающая первой, окажется из Китая, равна
 Ответ: 0,25.
Ответ: 0,25.
| | | Тип
| Условие
| | B6
| B 6 № 282856. В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Решение.
в среднем из 1000 садовых насосов, поступивших в продажу, 1000 − 5 = 995 не подтекают. Значит, вероятность того, что один случайно выбранный для контроля насос не подтекает, равна
 Ответ: 0,995.
Ответ: 0,995.
| | | Тип
| Условие
| | B6
| B 6 № 282857. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Решение.
По условию на каждые 100 + 8 = 108 сумок приходится 100 качественных сумок. Значит, вероятность того, что купленная сумка окажется качественной, равна
 Ответ: 0,93.
Ответ: 0,93.
| | | Тип
| Условие
| | B6
| B 6 № 282858. В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Решение.
Всего в соревнованиях принимает участие 4 + 7 + 9 + 5 = 25 спортсменов. Значит, вероятность того, что спортсмен, который выступает последним, окажется из Швеции, равна
 Ответ: 0,36.
Ответ: 0,36.
| | | Тип
| Условие
| | B6
| B 6 № 285922. Научная конференция проводится в 5 дней. Всего запланировано 75 докладов — первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции?
Решение.
За первые три дня будет прочитан 51 доклад, на последние два дня планируется 24 доклада. Поэтому на последний день запланировано 12 докладов. Значит, вероятность того, что доклад профессора М. окажется запланированным на последний день конференции, равна
 Ответ: 0,16.
Ответ: 0,16.
| | | Тип
| Условие
| | B6
| B 6 № 285923. Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны. В первый день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
Решение.
На третий день запланировано  выступлений. Значит, вероятность того, что выступление представителя из России окажется запланированным на третий день конкурса, равна выступлений. Значит, вероятность того, что выступление представителя из России окажется запланированным на третий день конкурса, равна
 Ответ: 0,225.
Ответ: 0,225.
| | | Тип
| Условие
| | B6
| B 6 № 285924. На семинар приехали 3 ученых из Норвегии, 3 из России и 4 из Испании. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Решение.
Всего в семинаре принимает участие 3 + 3 + 4 = 10 ученых, значит, вероятность того, что ученый, который выступает восьмым, окажется из России, равна 3:10 = 0,3.
Ответ: 0,3.
| | | Тип
| Условие
| | B6
| B 6 № 285925. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
Решение.
В первом туре Руслан Орлов может сыграть с 26 − 1 = 25 бадминтонистами, из которых 10 − 1 = 9 из России. Значит, вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России, равна
 Ответ: 0,36.
Ответ: 0,36.
| | | Тип
| Условие
| | B6
| B 6 № 285926. В сборнике билетов по биологии всего 55 билетов, в 11 из них встречается вопрос по ботанике. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике.
Решение.
Вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по ботанике, равна
 Ответ: 0,2.
Ответ: 0,2.
| | | Тип
| Условие
| | B6
| B 6 № 285927. В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по неравенствам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам.
Решение.
Из 25 билетов 15 не содержат вопроса по неравенствам, поэтому вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по неравенствам, равна
 Ответ: 0,6.
Ответ: 0,6.
| | | Тип
| Условие
| | B6
| B 6 № 285928. На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 8 прыгунов из России и 9 прыгунов из Парагвая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что шестым будет выступать прыгун из Парагвая.
Решение.
Вероятность того, что шестым будет выступать прыгун из Парагвая, равна
 Ответ: 0,36.
Ответ: 0,36.
| | | Тип
| Условие
| | B6
| B 6 № 320169. Вася, Петя, Коля и Лёша бросили жребий — кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя.
Решение.
Жребий начать игру может выпасть каждому из четырех мальчиков. Вероятность того, что это будет именно Петя, равна одной четвертой.
Ответ: 0,25.
| | | Тип
| Условие
| | B6
| B 6 № 320170. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп:
1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе?
Решение.
Вероятность того, что команда России окажется во второй группе, равна отношению количества карточек с номером 2, к общему числу карточек. Тем самым, она равна
 Ответ: 0,25.
Ответ: 0,25.
| | | Тип
| Условие
| | B6
| B 6 № 320178. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной?
Решение.
На клавиатуре телефона 10 цифр, из них 5 четных: 0, 2, 4, 6, 8. Поэтому вероятность того, что случайно будет нажата четная цифра равна 5: 10 = 0,5.
Ответ: 0,5.
| | | Тип
| Условие
| | B6
| B 6 № 320179. Какова вероятность того, что случайно выбранное натуральное число от 10 до 19 делится на три?
Решение.
Натуральных чисел от 10 до 19 десять, из них на три делятся три числа: 12, 15, 18. Следовательно, искомая вероятность равна 3:10 = 0,3.
Ответ: 0,3.
| | | Тип
| Условие
| | B6
| B 6 № 320181. В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин?
Решение.
Всего туристов пять, случайным образом из них выбирают двоих. Вероятность быть выбранным равна 2: 5 = 0,4.
Ответ: 0,4.
| | | Тип
| Условие
| | B6
| B 6 № 320183. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
Решение.
Обозначим «1» ту сторону монеты, которая отвечает за выигрыш жребия «Физиком», другую сторону монеты обозначим «0». Тогда благоприятных комбинаций три: 110, 101, 011, а всего комбинаций 23 = 8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, искомая вероятность равна:
 Ответ: 0,375.
Ответ: 0,375.
| | | Тип
| Условие
| | B6
| B 6 № 320184. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «А = сумма очков равна 5»?
Решение.
Сумма очков может быть равна 5 в четырех случаях: «3 + 2», «2 + 3», «1 + 4», «4 + 1».
Ответ: 4.
| | | Тип
| Условие
| | B6
| B 6 № 320185. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что в первый раз выпадает орёл, а во второй — решка.
Решение.
Всего возможных исходов — четыре: орел-орел, орел-решка, решка-орел, решка-решка. Благоприятным является один: орел-решка. Следовательно, искомая вероятность равна 1: 4 = 0,25.
Ответ: 0,25.
| | | Тип
| Условие
| | B6
| B 6 № 320186. На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
Решение.
Общее количество выступающих на фестивале групп для ответа на вопрос неважно. Сколько бы их ни было, для указанных стран есть 6 способов взаимного расположения среди выступающих (Д — Дания, Ш — Швеция, Н — Норвегия):
...Д...Ш...Н...,...Д...Н...Ш...,...Ш...Н...Д...,...Ш...Д...Н...,...Н...Д...Ш...,...Н...Ш...Д...
Дания находится после Швеции и Норвегии в двух случаях. Поэтому вероятность того, что группы случайным образом будут распределены именно так, равна
 Ответ: 0,33.
Замечание.
Пусть требуется найти вероятность того, что датские музыканты окажутся последними среди
Ответ: 0,33.
Замечание.
Пусть требуется найти вероятность того, что датские музыканты окажутся последними среди  выступающих от разных государств групп. Поставим команду Дании на последнее место и найдем количество перестановок без повторений из выступающих от разных государств групп. Поставим команду Дании на последнее место и найдем количество перестановок без повторений из  предыдущих групп: оно равно предыдущих групп: оно равно  Общее количество перестановок из всех Общее количество перестановок из всех  групп равно групп равно 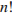 Поэтому искомая вероятность равна Поэтому искомая вероятность равна

| | | Тип
| Условие
| | B6
| B 6 № 320189. В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных.
Решение.
Из 5000 тысяч новорожденных 5000 − 2512 = 2488 девочек. Поэтому частота рождения девочек равна
 Ответ: 0,498.
Ответ: 0,498.
| | | Тип
| Условие
| | B6
| B 6 № 320190. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест.
Решение.
В самолете 12 + 18 = 30 мест удобны пассажиру В., а всего в самолете 300 мест. Поэтому вероятность того, что пассажиру В. достанется удобное место равна 30: 300 = 0,1.
Ответ: 0,1.
| | | Тип
| Условие
| | B6
| B 6 № 320191. На олимпиаде в вузе участников рассаживают по трём аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 250 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
Решение.
Всего в запасную аудиторию направили 250 − 120 − 120 = 10 человек. Поэтому вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории, равна 10: 250 = 0,04.
Ответ: 0,04.
| | | Тип
| Условие
| | B6
| B 6 № 320192. В классе 26 человек, среди них два близнеца — Андрей и Сергей. Класс случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.
Решение.
Пусть один из близнецов находится в некоторой группе. Вместе с ним в группе окажутся 12 человек из 25 оставшихся одноклассников. Вероятность того, что второй близнец окажется среди этих 12 человек, равна 12: 25 = 0,48.
| | | Тип
| Условие
| | B6
| B 6 № 320193. В фирме такси в наличии 50 легковых автомобилей; 27 из них чёрные с жёлтыми надписями на бортах, остальные — жёлтые с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями.
Решение.
Машин желтого цвета с черными надписями 23, всего машин 50. Поэтому вероятность того, что на случайный вызов приедет машина желтого цвета с черными надписями, равна:

| | | Тип
| Условие
| | B6
| B 6 № 320194. В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
Решение.
На первом рейсе 6 мест, всего мест 30. Тогда вероятность того, что турист П. полетит первым рейсом вертолёта, равна:
 Ответ: 0,2.
Ответ: 0,2.
| | | Тип
| Условие
| | B6
| B 6 № 320195. Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0,045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
Решение.
Частота (относительная частота) события «гарантийный ремонт» равна 51: 1000 = 0,051. Она отличается от предсказанной вероятности на 0,006.
Ответ: 0,006.
| | | Тип
| Условие
| | B6
| B 6 № 320208. В кармане у Миши было четыре конфеты — «Грильяж», «Белочка», «Коровка» и «Ласточка», а также ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».
Решение.
В кармане было 4 конфеты, а выпала одна конфета. Поэтому вероятность этого события равна одной четвертой.
Ответ: 0,25.
| | | Тип
| Условие
| | B6
| B 6 № 320209. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 10, но не дойдя до отметки 1 час.
Решение.
На циферблате между десятью часами и одним часом три часовых деления. Всего на циферблате 12 часовых делений. Поэтому искомая вероятность равна:
 Ответ: 0,25.
Ответ: 0,25.
| | | Тип
| Условие
| | B6
| B 6 № 500997. В классе учится 21 человек. Среди них две подруги: Аня и Нина. Класс случайным образом делят на 7 групп, по 3 человека в каждой. Найти вероятность того. что Аня и Нина окажутся в одной группе.
Решение.
Пусть Аня оказалась в некоторой группе. Тогда для 20 оставшихся учащихся оказаться с ней в одной группе есть две возможности. Вероятность этого события равна 2: 20 = 0,1.
Приведем комбинаторное решение.
Всего способов выбрать 3 учащихся из 21 учащегося класса равно  . Выбрать пару «Аня и Нина» и поместить их в одну из семи групп можно . Выбрать пару «Аня и Нина» и поместить их в одну из семи групп можно 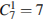 способами. Добавить в эту группу еще одного из оставшихся 19 учащихся можно способами. Добавить в эту группу еще одного из оставшихся 19 учащихся можно  способами. Поэтому вероятность того, что девочки окажутся в одной группе равна способами. Поэтому вероятность того, что девочки окажутся в одной группе равна
 Приведем еще одно решение.
Рассмотрим первую группу. Вероятность того, что Аня окажется в ней, равна
Приведем еще одно решение.
Рассмотрим первую группу. Вероятность того, что Аня окажется в ней, равна  . Если Аня уже находится в первой группе, то вероятность того, что Нина окажется этой же группе равна . Если Аня уже находится в первой группе, то вероятность того, что Нина окажется этой же группе равна  . Поскольку все семь групп равноправны, вероятность того, что подруги окажутся в одной группе, равна . Поскольку все семь групп равноправны, вероятность того, что подруги окажутся в одной группе, равна
 Ответ: 0,1.
Ответ: 0,1.
| | | Тип
| Условие
| | B6
| B 6 № 501190. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что выпадет хотя бы две решки.
Решение.
Всего возможных исходов — 8: орел-орел-орел, орел-орел-решка, орел-решка-решка, орел-решка-орел, решка-решка-решка, решка-решка-орел, решка-орел-орел, решка-орел-решка. Благоприятными являются четыре: решка-решка-решка, решка-решка-орел, решка-орел-решка, орел-решка-решка. Следовательно, искомая вероятность равна 4: 8 = 0,5.
Ответ: 0,5.
| |
Не нашли, что искали? Воспользуйтесь поиском:
|

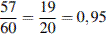 .
Ответ: 0,95.
.
Ответ: 0,95.
 .
Ответ: 0,4.
.
Ответ: 0,4.
 .
Ответ: 0,25.
.
Ответ: 0,25.
 Ответ: 0,14.
Ответ: 0,14.
 .
Ответ: 0,5.
.
Ответ: 0,5.
 спортсменок из Китая. Тогда вероятность того, что спортсменка, выступающая первой, окажется из Китая, равна
спортсменок из Китая. Тогда вероятность того, что спортсменка, выступающая первой, окажется из Китая, равна
 Ответ: 0,25.
Ответ: 0,25.
 Ответ: 0,995.
Ответ: 0,995.
 Ответ: 0,93.
Ответ: 0,93.
 Ответ: 0,36.
Ответ: 0,36.
 Ответ: 0,16.
Ответ: 0,16.
 выступлений. Значит, вероятность того, что выступление представителя из России окажется запланированным на третий день конкурса, равна
выступлений. Значит, вероятность того, что выступление представителя из России окажется запланированным на третий день конкурса, равна
 Ответ: 0,225.
Ответ: 0,225.
 Ответ: 0,2.
Ответ: 0,2.
 Ответ: 0,6.
Ответ: 0,6.
 Ответ: 0,25.
Ответ: 0,25.
 Ответ: 0,375.
Ответ: 0,375.
 Ответ: 0,33.
Замечание.
Пусть требуется найти вероятность того, что датские музыканты окажутся последними среди
Ответ: 0,33.
Замечание.
Пусть требуется найти вероятность того, что датские музыканты окажутся последними среди  выступающих от разных государств групп. Поставим команду Дании на последнее место и найдем количество перестановок без повторений из
выступающих от разных государств групп. Поставим команду Дании на последнее место и найдем количество перестановок без повторений из  предыдущих групп: оно равно
предыдущих групп: оно равно  Общее количество перестановок из всех
Общее количество перестановок из всех 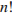 Поэтому искомая вероятность равна
Поэтому искомая вероятность равна

 Ответ: 0,498.
Ответ: 0,498.

 Ответ: 0,2.
Ответ: 0,2.
 Ответ: 0,25.
Ответ: 0,25.
 . Выбрать пару «Аня и Нина» и поместить их в одну из семи групп можно
. Выбрать пару «Аня и Нина» и поместить их в одну из семи групп можно 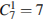 способами. Добавить в эту группу еще одного из оставшихся 19 учащихся можно
способами. Добавить в эту группу еще одного из оставшихся 19 учащихся можно  способами. Поэтому вероятность того, что девочки окажутся в одной группе равна
способами. Поэтому вероятность того, что девочки окажутся в одной группе равна
 Приведем еще одно решение.
Рассмотрим первую группу. Вероятность того, что Аня окажется в ней, равна
Приведем еще одно решение.
Рассмотрим первую группу. Вероятность того, что Аня окажется в ней, равна  . Если Аня уже находится в первой группе, то вероятность того, что Нина окажется этой же группе равна
. Если Аня уже находится в первой группе, то вероятность того, что Нина окажется этой же группе равна  . Поскольку все семь групп равноправны, вероятность того, что подруги окажутся в одной группе, равна
. Поскольку все семь групп равноправны, вероятность того, что подруги окажутся в одной группе, равна
 Ответ: 0,1.
Ответ: 0,1.