
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Натуральные уравнения пространственной кривой
Лекция № 6 от 19.03.14.
Кривизна кривой.
Окружность большого радиуса воспринимается менее искривленной, чем окружность с маленьким радиусом. А прямая линия не имеет искривлений. Попытаемся дать количественную оценку понятия кривизна.
Что бы подойти к точному определению заметим, что чем сильнее искривление, тем быстрее меняет свое направление касательная. Поэтому в качестве меры искривления целесообразно брать угол поворота касательной, или точнее скорость угла поворота касательной.
Рассмотрим кривую  в двух точках М(s) и L(s+ Δ s). Пусть UМL=Δ s,
в двух точках М(s) и L(s+ Δ s). Пусть UМL=Δ s,
Векторы касательной в этих точках  и
и  , и угол между ними Δ φ.
, и угол между ними Δ φ.
Определение: Кривизной кривой в точке называется величина k 1 =  .
.
Замечание: Другими словами кривизной кривой называется скорость изменения угла касательной.
Перенесем векторы  и
и  в одну точку – А, и рассмотрим ΔАВС:
в одну точку – А, и рассмотрим ΔАВС: 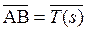 ,
,  ,
,  , тогда Δ φ= ÐВАС, АВ = АС = 1 и
, тогда Δ φ= ÐВАС, АВ = АС = 1 и  .
.
Обозначим середину ВС - К, тогда по свойствами равнобедренного треугольника: ВС = 2·ВК = 2·АВ· sin 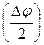 = 2· sin
= 2· sin 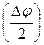 и
и

При Δ s → 0 угол между касательными Δ φ→ 0, тогда sin (Δ φ) ≈ Δ φ.
k 1 = 

Т.о. k 1 = 
Т.к.  , тогда
, тогда
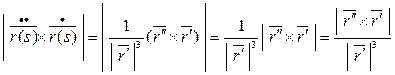
С другой стороны  .
.
Т.о. кривизна кривой, заданной в произвольной параметризации можно найти по формуле: 
Замечание: Кривизна кривой всегда не отрицательна, k 1 ≥ 0.
Определение: Если в точке кривизна равна 0. то точка называется точкой распрямления.
Для точек распрямления k 1 = 0, а значит  .
.
Теорема: Для того, чтобы линия была прямой необходимо и достаточно, чтобы её кривизна в любой точке равнялась 0.
Доказательство:
Необходимость. Если линия прямая, тогда


 k 1 = 0.
k 1 = 0.
Достаточность. k 1 = 0 

 - это и есть прямая.
- это и есть прямая.
Определение: Величину R =  называют радиусом кривизны.
называют радиусом кривизны.
Кручение кривой
Рассмотрим кривую  в двух точках М(s) и L(s+ Δ s). Пусть UМL=Δ s,
в двух точках М(s) и L(s+ Δ s). Пусть UМL=Δ s,
Векторы бинормали в этих точках  и
и  , и угол между ними Δ θ я вляется углом между соприкасающимися плоскостями.
, и угол между ними Δ θ я вляется углом между соприкасающимися плоскостями.
Определение: Абсолютным кручением называется | k 2 |=  .
.
Замечание: Другими словами кручением кривой называется скорость изменения угла соприкасающейся плоскости.
Перенесем векторы  и
и  в одну точку – А, и рассмотрим ΔАDС:
в одну точку – А, и рассмотрим ΔАDС:  ,
,  ,
, 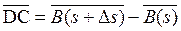 , тогда Δ θ= ÐDАС, АD = АС = 1 и
, тогда Δ θ= ÐDАС, АD = АС = 1 и  .
.
Обозначим середину DС - К, тогда по свойствами равнобедренного треугольника: DС = 2·СК = 2·АС· sin 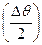 = 2· sin
= 2· sin 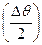 и
и

При Δ s → 0 угол между касательными Δ θ→ 0, тогда sin (Δ θ) ≈ Δ θ.
| k 2 |= 

Т.о. | k 2 |= 
Т.к.  - вектор единичной длины
- вектор единичной длины 

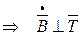
 т.е.
т.е. 
Т.к. | k 2 |= 
 λ = ± | k 2 |
λ = ± | k 2 | 

Определение: Кручением кривой называется величина k 2 = ± | k 2 |, которая берется со знаком плюс, если вращение соприкасающейся плоскости направлено от 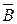 к
к  , и со знаком минус, если вращение от
, и со знаком минус, если вращение от  к
к 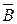 .
.
В формуле  возьмем знак минус
возьмем знак минус 


Т.о. 
Для произвольной параметризации:
Т.к. 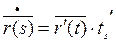

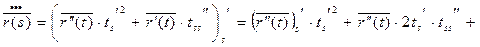



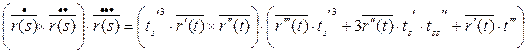



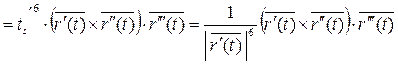


Теорема: Для того, что бы кривая γ была плоской необходимо и достаточно, чтобы кручение в любой точке равнялось 0.
Доказательство:
Необходимость. Если кривая плоская, отсюда следует, что соприкасающаяся плоскость для любой точки одна и та же и совпадает с плоскостью кривой.  , а так как
, а так как  , тогда k 2 = 0.
, тогда k 2 = 0.
Достаточность. Если k 2 = 0  .
.
Т.к. 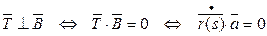

Т.е. если  и
и 
 - уравнение плоскости.
- уравнение плоскости.
Вывод: Вычислительные формулы для кривизны и кручения
| Кривизна | Кручение | |
| естественная параметризация | 
| 
|
| произвольная параметризация | 
| 
|
Задача. Найти кривизну и кручение для кривой, заданной явным уравнением у=f (х).
Решение. Так как уравнение явное, то кривая плоская, а значит ее кручение равно 0.
Для нахождения кривизны перейдем к параметрическому уравнению


 и
и 

Задача. Найти кривизну для плоской кривой, заданной параметрическими уравнениями х = х (t) у = у (t).
Решение. Для нахождения кривизны перейдем к параметрическим уравнениям в пространстве


 и
и 

Формулы Френе
Пусть γ - кривая заданная естественной параметризацией  в окрестности точки М0(s 0). Пусть векторы
в окрестности точки М0(s 0). Пусть векторы 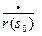 и
и  не коллинеарны и отличны от нулевого вектора. Векторы
не коллинеарны и отличны от нулевого вектора. Векторы  - попарно перпендикулярные единичные векторы сопровождающего трехгранника. При изменении s на Δ s получим три векторных функций
- попарно перпендикулярные единичные векторы сопровождающего трехгранника. При изменении s на Δ s получим три векторных функций  .
.
Причем:

 и
и  , т.к.
, т.к.  и
и 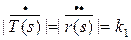
Т.к.  и
и 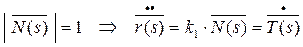
 - первая формула Френе.
- первая формула Френе.
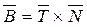 - продифференцируем по s.
- продифференцируем по s.

Т.к.  и
и  (
(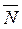 - вектор единичной длины)
- вектор единичной длины) 
Т.е.  k 2:
k 2:  .
.
Таким образом, получаем  - третья формула Френе.
- третья формула Френе.

 - вторая формула Френе.
- вторая формула Френе.
Таким образом, получили:
первая формула Френе 
вторая формула Френе 
третья формула Френе 
Для запоминания

Замечание: Формулы Френе показывают зависимость между векторами  и их производными. Т.е. единичные векторы сопровождающего трехгранника играют роль базиса, коэффициентами разложения по этому базису выступают кривизна и кручение.
и их производными. Т.е. единичные векторы сопровождающего трехгранника играют роль базиса, коэффициентами разложения по этому базису выступают кривизна и кручение.
Достаточно ли знать только кривизну и кручение для задания кривой?
Натуральные уравнения пространственной кривой
Рассмотрим кривую γ заданную естественной параметризацией  в окрестности некоторой точки М. Кривизна k 1 и кручение k 2 являются функциями от s - k 1 = k 1(s), k 2 = k 2(s). (*)
в окрестности некоторой точки М. Кривизна k 1 и кручение k 2 являются функциями от s - k 1 = k 1(s), k 2 = k 2(s). (*)
Будем считать, что k 1 ≠0 - нет точек распрямления. Т.к. длина дуги не зависит от выбора системы координат, то и вид функций k 1(s) и k 2(s)не зависит от выбора системы координат.
Определение: Уравнения k 1 = k 1(s), k 2 = k 2(s) называются, натуральными уравнениями пространственной кривой.
Теорема: Для того, что бы две кривые γ1 и γ2 отличались лишь положением в пространстве, необходимо и достаточно, чтобы их натуральные уравнения были одинаковыми (после согласования начал отсчета и направлений).
Доказательство: Необходимость: γ1 и γ2 - отличаются положением в пространстве, отсюда следует, что существуют повороты и параллельный перенос координатных осей.
Согласуем начало отсчета и направление М01 и М02, М11 и М22, причем  М01М11=
М01М11=  М02М22 = Δ s.
М02М22 = Δ s.
Угол между касательными остается постоянным Δ φ 1=Δ φ 2  .
.
Угол между бинормалями остается постоянным, значит Δ ϑ 1=Δ ϑ 2  .
.
 вид функциональной зависимости k 1(s) и k 2(s)обоих кривых одинаков.
вид функциональной зависимости k 1(s) и k 2(s)обоих кривых одинаков.
Достаточность: без доказательства.
Теорема: Если есть две произвольные функции φ (s)≥0 и ψ (s) - непрерывные  s
s  (s 1, s 2), то существует пространственная кривая, для которой k 1= φ (s) и k 2= ψ (s). Кривая будет определена с точностью до положения в пространстве.
(s 1, s 2), то существует пространственная кривая, для которой k 1= φ (s) и k 2= ψ (s). Кривая будет определена с точностью до положения в пространстве.
 По формулам Френе
По формулам Френе
-система из 9 линейных дифференциальных
уравнений для скалярных функций
(координатных).
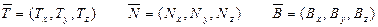 (для каждой координаты), тогда
(для каждой координаты), тогда 
 искомая кривая. (без доказательства).
искомая кривая. (без доказательства).
Основная теорема.

Выполним разложение  в ряд Тейлора.
в ряд Тейлора.
 , где
, где  функции
функции 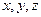 - непрерывны и дифференцируемы в достаточное число раз. Отсюда следует, что они ограничены:
- непрерывны и дифференцируемы в достаточное число раз. Отсюда следует, что они ограничены:  < ограничен по модулю.
< ограничен по модулю.  >0 постоянная одинаковая для
>0 постоянная одинаковая для  .
.
Т.е. 
 <
< 
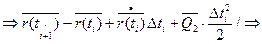

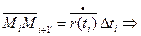
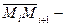


один из  оценили максимумом
оценили максимумом

| <== предыдущая лекция | | | следующая лекция ==> |
| Вторая — поддержание «спонтанного сотрудничества» во всей общественной структуре. | | | Элементарная поверхность |
Не нашли, что искали? Воспользуйтесь поиском: