Непрерывная случайная величина Х задана плотностью распределения вероятностей . Тогда математическое ожидание этой нормально распределенной случайной величины равно

А. 3

В. 18

С. 4

128. НРСВ Х задана плотностью распределения:f(x). Математическое ожидание m и дисперсия D этой СВ равны

А. m=1, D=25

В. m=5, D=1

С. m=5, D=25

129. Правило трех сигм означает, что:

А. Вероятность попадания СВ в интервал, то есть близка к единице

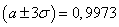
В. НРСВ не может выйти за пределы

С. График плотности НРСВ симметричен относительно математического ожидания

130. СВ Х распределена нормально с математическим ожиданием, равным 5 и СКО, равным 2 единицы. Выражение для плотности распределения этой НРСВ имеет вид:

А

В

С

131. НРСВ Х имеет математическое ожидание a=10 и СКО =5. С вероятностью 0,9973 величина Х попадет в интервал:

А. (5; 15)

В. (0; 20)

С. (-5; 25)

Не нашли, что искали? Воспользуйтесь поиском: