Краткие теоретические сведения. В 1923 г. французский физик Лу и де Бройль высказал гипотезу, согласно которой корпус­кулярно - волновой дуализм является универсальным свой­ством любых

В 1923 г. французский физик Лу и де Бройль высказал гипотезу, согласно которой корпус­кулярно - волновой дуализм является универсальным свой­ством любых материальных объектов, а не только света. Фотон — не единственная элементарная частица в микроми­ре. Любая микрочастица обладает помимо корпускулярных еще волновыми свойствами. Это значит, что частица массой m, движущаяся со скоростью υ, характеризуется не только координатами, импульсом р и энергией Е, но и подобно фо­тону частотой ν и длиной волны λ:

Е = h×ν (1.1)

Любой частице, обладающей импульсом р, соответст­вует длина волны де Бройля:

(1.2)

где λ - длина волны, м; h - постоянная Планка; Дж·c^[1]; р - импульс, кг·м/с; κ - волновой вектор, рад · м ^-1.

Наличие волновых свойств у микрочастиц означает, что можно наблюдать их интерференцию и дифракцию.

Подтвержденная на опыте идея де Бройля о двойственной природе микрочастиц — корпускулярно - волновом дуализме — принципиально изменила представление об облике микромира. Поскольку всем микрообъектам присущи и корпускулярные и волновые свойства, то, очевидно, любую из этих «частиц» нельзя считать ни частицей, ни волной в классическом понимании. Возникла потребность в такой теории, в которой волновые и корпускулярные свойства материи выступали бы не как исключающие, а как взаимно дополняющие друг друга. В основу такой теории — волновой, или квантовой, механики и легла концепция де Бройля. Это отражается даже в названии волновая функция для величины, описывающей в этой теории состояние системы. Квадрат модуля волновой функции определяет вероятность состояния системы, и поэтому о волне де Бройля говорят как о волнах вероятности (точнее, амплитуд вероятности). Для свободной частицы с точно заданным импульсом, движущейся вдоль оси х, волновая функция имеет вид:

Ψ(x,t)= Ψ₀× 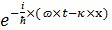(1.3)

Квадрат модуля волновой функции |Ψ(x,t)|² определяет вероятность нахождения частицы в момент времени t в точке с координатой х. Волновая функция является функцией координат и времени и может быть найдена путем решения уравнения:

і×ћ× (1.4)

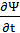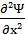где і - мнимая единица; ћ =h / 2×π - редуцированная постоянная Планка; − производная по времени t; m — масса частицы; − вторая производная по координате x; U – потенциальная энергия частицы, Дж;Ψ(х,t)-волновая функция.
Это нерелятивистское волновое уравнение Шредингера для одномерного случая.

Уравнение Шредингера не выводится, а вводится как новый принцип, или постулат, и затем следствия из него проверяются на эксперименте.

Необходимые требования к уравнению Шредингера:

1) Уравнение должно быть линейным, т.к. должен выполняться принцип суперпозиции.

2) Уравнение должно содержать только фундаментальные константы в качестве коэффициентов, например такие константы как e, m, ћ.

3) В уравнение не должны явно входить параметры движения, например координата или скорость υ.

Итак, уравнение Шредингера - основное динамическое уравнение нерелятивистской волновой механики, играет такую же важную роль, как уравнения Ньютона в классической механике и уравнения Максвелла в теории электромагнитного поля [2].

Релятивистское уравнения для волновой функции является уравнение Клейна-Гордона, то есть удовлетворяющее требованиям относительности теории уравнение для частиц со спином нуль.

Для свободной частицы уравнение Клейна – Гордона записывается в виде:

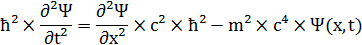( 1.5)

где ћ =h / 2×π - редуцированная постоянная Планка (постоянная Дирака);

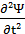− вторая производная по времени t; 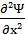− вторая производная по координате x; с — скорость света в вакууме, равна 3×10⁸ м/c; m — масса частицы; ⁻ волновая функция.

Решением уравнения является функция Ψ (х,t), зависящая только от координаты (х) и времени (t). Следовательно, частицы, описываемые этой функцией, не обладают никакими дополнительными внутренними степенями свободы, т. е. действительно являются бесспиновыми. [1].

1.2 Дифракция фотонов

Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями (например, вблизи границ непрозрачных тел, сквозь малые отверстия и т.п.) и связанных с отклонениями от законов геометрической оптики. В частности, дифракция приводит к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Явление дифракции заключается в перераспределении светового потока в результате суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно.

Распространение света в виде потока фотонов и квантовый характер взаимодействия света с веществом подтверждены в многочисленных экспериментах. Казалось бы, это является убедительным доказательством квантовых представлений о свойствах света. Однако целый ряд оптических явлений (поляризация, интерференция, дифракция) неопровержимо свидетельствуют о волновых свойствах света [3].

Прямым подтверждением этого явились опыты 1909 г. Джофри Тейлора по наблюдению дифракции поочередно летящих одиночных фотонов. Для этого интенсивность света, падающего на щель, следовало существенно понизить (например, как в экспериментах Тэйлора - с помощью светофильтров). Ослабление интенсивности означает уменьшения числа N_фпадающих на щель фотонов. В результате можно на столько уменьшитьN_ф, что фотоны будут следовать друг за другом с интервалом времени, на несколько порядков превышающим время, за которое фотон попадает на фотопластинку ФП, помещенную за щелью на расстоянии L. На рисунке 1 показан опыт по дифракции одиночных фотонов на щели.

Ход работы:

Не нашли, что искали? Воспользуйтесь поиском: