Побудова трикутника з даними сторонами a, b, c.

Курсова робота

З математики

на тему: «Розв’язання задачі Аполлонія»

Студентки 33-М групи

напрям підготовки 6.040201 Математика

Пуди Тетяни Петрівни

Науковий керівник:

кандидат педагогічних наук

Заїка О. В.

Національна шкала_________________

Кількість балів: _______Оцінка: ECTS ________

Члени комісії _____________ _______________

(підпис) (прізвище та ініціали)

_____________ ________________

(підпис) (прізвище та ініціали

Глухів – 2016

ЗМІСТ

ВСТУП……………………………………………………………………………. 3

РОЗДІЛ I ТЕОРЕТИЧНИЙ АНАЛІЗ РОЗВ’ЯЗАННЯ ГЕОМЕТРИЧНИХ ЗАДАЧ НА ПОБУДОВУ……………………………………………………......5

1.1 Біографія та творчий доробок Аполлонія Пергського.……………….. 5

1.2 Етапи розв’язування геометричних задач на побудову.………………..9

1.3 Основні геометричні побудови ………………………………………….14

РОЗДІЛ II ПРАКТИЧНИЙ АНАЛІЗ ЗАСТОСУВАННЯ ЗАДАЧІ АПОЛЛОНІЯ………………………………………………………………….. 19

2.1 Частинні випадки задачі Аполлонія. ………………………………….... 19

2.2 Розв’язання задачі Аполлонія. …………………………………….…… 23

2.3 Розв’язання задач методом гіпербол які перетинаються и алгебраїчним методом…………………………………………………………………………26

ВИСНОВОК…………………………………………………………………… 30

ЛІТЕРАТУРА………………………………………………………………… 32

ДОДАТКИ

Мета дослідження: з’ясувати основні найпростіші побудови задач в курсі геометрії та етапи їх розв’язування; дослідити розв’язання задачі Аполлонія.

Постановка мети зумовила такі завдання:

· розглянути біографію Аполлонія Пергського;

· з’ясувати етапи розв’язання на побудову;

· розв’язати основні задачі на побудову;

· переглянути розв’язання допоміжних задач для основної задачі Аполлонія;

· розв’язання основної задачі Аполлонія методом інверсії;

· з’ясувати які ще є методи розв’язання задачі Аполлонія.

Об’єкт дослідження -задачі Аполлонія.

Предмет дослідження – методи розв’язання задачі Аполлонія.

Основними методами дослідження є: пошуково-біографічний метод: вивчення архівних, фондів, описів, біографічних видань; історико-математичний, порівняльний та статистичний аналіз фактів та явищ, їх синтез для дослідження розв’язання задач Аполлонія; предметно-цільовий аналіз математичної літератури і підручників, де розглядалися методи дослідження задач на побудову; теоретичне узагальнення та порівняння опрацьованих матеріалів для формулювання висновків і визначення можливостей творчого використання на сучасному етапі розвитку освіти в Україні.

Курсова робота складається з вступу, двох розділів, трьох додатків та 39 рисунків.

РОЗДІЛ I ТЕОРЕТИЧНИЙ АНАЛІЗ РОЗВ’ЯЗАННЯ ГЕОМЕТРИЧНИХ ЗАДАЧ НА ПОБУДОВУ

1.1 Біографія та творчий доробок Аполлонія Пергського.

Відомості про життя Аполлонія практично відсутні. Народився він в малоазіатському місті Перга. Ще в ранній молодості приєднався до Олександрійської математичної школи Евкліда і згодом викладав там як визнаний авторитет в геометрії й астрономії. В кінці життя на деякий час повернувся на батьківщину, де були відкриті навчальний центр та бібліотека, аналогічні Александріївському мусейону. У тексті праць Аполлонія виявлено згадку про його сина, якого також звали Аполлоній [1, с. 70-72]. Нам не вдалося з’ясувати точної дати смерті, але помер учений в Олександрії.

Нами з’ясовано, що Аполлоній прославився в першу чергу монографією «Конічні перерізи» (8 книг), в якій дав змістовну загальну теорію еліпса, параболи і гіперболи. Саме Аполлоній запропонував загальноприйняті назви цих кривих; до нього їх називали просто «перетинами конуса». Книга мала величезний вплив на творчість наступних математиків, включаючи Ферма, Декарта, Ньютона, Лагранжа і багатьох інших. Багато теорем Аполлонія, особливо про максимум, еволюту, нормаль і т. п. увійшли в сучасні підручники з диференціальної геометрії конічних перерізів.

Яким чином Аполлоній, не володіючи математичним аналізом, зумів зробити свої відкриття, неясно. Можливо, у нього, як у Архімеда, був якийсь метод нескінченно малих, який він використовував в евристичних цілях, щоб потім передовести результат канонічними засобами геометрії. Ван дер Варден пише: «Аполлоній віртуозно володіє геометричною алгеброю, але не менш віртуозно вміє приховувати свій первісний хід думок. Через це його книгу і важко розуміти; міркування його елегантні і кристально ясні, але що його привело саме до таких міркувань, а не до якихось інших,- про це можна лише здогадуватись» [2, с. 338-339].

До відкриттів Кеплера і Ньютона теорія Аполлонія практично застосовувалася в основному для вирішення кубічних рівнянь, а також в оптиці дзеркал. Коли виявилося, що орбіта матеріальної частинки в задачі двох тіл є одне з конічних перерізів, інтерес до даних кривих різко зріс, і праці Аполлонія були продовжені на новому математичному рівні [3, с. 48]. Він ввів і інші математичні терміни, латинські аналоги яких назавжди увійшли в науку, зокрема: асимптота, абсциса, ордината, апліката.

З інших заслуг Аполлонія перед наукою, відзначимо, що він переробив астрономічну модель Евдокса, ввівши епіцикли і ексцентрики для пояснення нерівномірності руху планет. Цю теорію пізніше розвинули Гіппарх і Птолемей. Він також знайшов розв’язання задачі про побудову кола, що дотикається до трьох заданих кіл («задача Аполлонія»), вивчав спіральні лінії, займався геометричною оптикою. Також з’ясовано, що на його честь названо кратер на Місяці.

В ході нашого дослідження було виявленно, що у VII книзі «Математичного збірника» Паппа надає короткий опис шести математичних трактатів Аполлонія:

Відсікання відношення (Λογου αποτομη) в двох книгах, що містять 180 теорем. Розглядається задача: дано дві прямі і на кожній зазначено по точці; дана також третя точка, що не збігається з першими двома, і потрібно провести через неї пряму так, щоб вона відтинала на заданих прямих відрізки (рахуючи від зазначених точок), що знаходяться в заданому відношенні.

Відсікання площі (Χωριου αποτομη) в двох книгах, що містять 124 теореми.

Певний перетин (Διωριςμενη τομη) - в двох книгах, що містять 83 теореми.

Вставки (Νευσεις) - в двох книгах, що містять 125 теорем.

Дотик (Επαφαι) - в двох книгах, що містять 60 теорем. У книзі вирішується відома проблема дотику Аполлонія: задані три об'єкти, кожен з яких може бути точкою, прямою або колом. Потрібно побудувати коло, яке дотикається всіх заданих об'єктів (для точки замість дотику потрібне проходження через неї).

Плоскі місця (Τοποι επιπεδοι) - в двох книгах, що містять 147 теорем.

З цих творів Аполлонія збереглося тільки перше - в середньовічному арабському перекладі. Папп написав також (частково дійшли до нас) коментарі до цих трактатів. В інших працях Папп згадує ще кілька творів Аполлонія:

Числа. Відгук на «Обчислення піщинок» Архімеда.

Про невпорядковані ірраціональності. Коментарі Паппи до цієї праці збереглися тільки в арабському перекладі. Судячи з них, Аполлоній досліджує класи ірраціональних чисел, не розглянуті в X книзі «Начал» Евкліда [4, с. 648].

Прокл Діадох в коментарі до I книги «Начал» Евкліда згадує трактат Аполлонія про «Гвинтові лінії» (Περι του κοχλιου). Імовірно тут розглядалися спіралі на поверхні циліндра [4, с. 648].

Так звана XIV книга «Начал» Евкліда, написана Гіпсіклом, являє собою коментар до твору Аполлонія: «Порівняння додекаедра з ікосаедром». Аполлоній доводить, що поверхні додекаедра та ікосаедра, вписаних в одну і ту ж сферу, відносяться так як і їх об’єми [4, с. 648].

Нарешті, Евдокій в коментарях до «Вимірювання кола» Архімеда згадує твір Аполлонія «Швидке отримання результатів» (Ωκυτοκιον). Тут Аполлоній змагається з Архімедом. Він описує більш зручну, ніж у Архімеда, систему іменування дуже великих чисел, а також більш швидкий, ніж запропонований Архімедом, алгоритм обчислення відношення довжини кола до її діаметра.

Спроби відновити втрачені твори Аполлонія за збереженими грецьким і арабськими згадками робили, крім Галлея, також Вієт (Дотик), Ферма (Плоскі місця) та інші [4, с. 649].

Давньогрецькі автори (наприклад, Клавдій Птолемей в XII книзі Альмагеста) згадували відкриття Аполлонія в астрономії, проте жодний його астрономічний твір не зберігся.

У двотомній книжці Аполлонія «Про дотики» було вміщено його знамениту задачу: «Дано три фігури, кожна з яких може бути точкою, прямою або колом. Побудувати коло, яке проходило б через дані точки (або точку) і дотикалося до даних кіл або прямих». Розв'язання задачі самим Аполлонієм до нас не дійшло, а конкретніше воно було втрачене. Пропоновані далі задачі на побудову — п'ять з десяти можливих окремих варіантів задачі Аполлонія. Легко побачити, що кожний варіант має кілька окремих випадків, залежно від розміщення даних фігур на площині [5, с. 150].

1.2 Етапи розв’язування геометричних задач на побудову.

Задача на побудову циркулем і лінійкою вважається розв’язаною, якщо вона зведена до виконання скінченного числа елементарних операцій, виконуваних циркулем і лінійкою. Такі елементарні операції ще називаються найпростішими (НП). Процес розв’язування задачі на побудову складається з чотирьох етапів: 1) пошук способу побудови (аналіз); 2) побудова шуканої фігури; 3) доведення правильності виконаної побудови; 4) дослідження побудови. Розглянемо ці етапи:

1. Пошук способу побудови починають з припущення про те, що задача розв’язана, тобто фігуру побудовано. Зображають відповідну фігуру на малюнку-ескізі і вивчають властивості побудованої фігури та її зв’язки з даними задачі, поки не встановлять послідовність побудов, яка приводить до розв’язання. Заключним моментом цього етапу є складання плану побудови і стислий його запис. У плані побудови перелічують у певній послідовності всі елементарні або основні побудови, які потрібно виконати для побудови шуканої фігури.

2. Побудова. Виконуємо побудову шуканої фігури циркулем і лінійкою за складеним планом. Якщо задача нескладна, то побудова фігури зводиться до виконання елементарних побудов. При розв’язуванні складних задач розчленовувати побудову на елементарні недоцільно, бо кількість елементарних побудов настільки зростає, що описання побудови стає громіздким. Тому практично побудову зводять не до елементарних побудов, а до деяких типових комбінацій елементарних побудов, які часто зустрічаються в процесі розв’язування. Типові комбінації елементарних побудов називаються основними задачами на побудову або основними побудовами.

3. Доведення в задачах на побудову ґрунтується на загальних положеннях (аксіомах, теоремах і властивостях геометричних фігур). Доводимо, що побудована фігура відповідає всім вимогам задачі: має задану форму (є рівнобедреним трикутником, паралелограмом, трапецією тощо) і розміри її елементів відповідають умові задачі. Доведення в задачах на побудову містить два види обґрунтувань – посилання на побудовані певні геометричні залежності і посилання на загальні положення. Використання в процесі доведення аргументів, здобутих у результаті виконання креслярських операцій, не знижує точність доведення. Це пояснюється тим, що кожний інструмент геометричної побудови характеризується рядом властивих цьому інструменту операцій, які можуть бути виражені в абстрактно-математичній формі системою аксіом.

4. Дослідження. Мета дослідження в задачах на побудову полягає в з’ясуванні трьох питань: 1. Чи при будь-якому виборі даних елементів задача має розв’язок? 2. При якому виборі даних вона не має розв’язку? 3. При якому виборі даних задача має розв’язки і скільки?

Один із способів дослідження в задачах на побудову – графічний. Він полягає ось у чому. Кожна геометрична фігура визначається сукупністю точок, які можна поділити на відомі і шукані (невідомі). Шукана точка має дві геометричні властивості, за кожною з яких ми відносимо цю точку до певного геометричного місця точок. Визначення всіх випадків взаємного розміщення цих двох геометричних місць на площині і є графічним дослідженням. Задача не матиме розв’язку, якщо відсутні спільні точки геометричних місць. І кожна точка, яка належить одразу двом геометричним місцям, може привести до розв’язку.

Розв’язування задачі на побудову, крім фактичних побудов, включає й логічні операції (аналіз, доведення, дослідження), виконання яких доцільно ілюструвати малюнками.

Перш ніж розв’язувати задачі на побудову, необхідно спочатку впевнитися, що даних елементів досить для виконання побудови, тобто встановити, чи задача визначена, невизначена, чи перевизначена.

Шуканими в задачах на побудову можуть бути: точка, пряма (відрізок), кут, коло або певна їх сукупність. Якою б не була задача на побудову, вона зводиться до послідовної побудови визначальних точок і відстаней між ними. Так, для побудови відрізка досить побудувати його кінці, трикутника – його вершини, кола – його центр і точку на колі.

Якщо шукана точка належить кожній з двох даних геометричних фігур, то вона або лежить на їх перетині, або є точкою їх дотику. Кількість розв’язків задачі визначається кількістю знайдених шуканих точок.

Названа схема розв’язування задачі на побудову не єдина. Іноді дослідження доцільно провести після аналізу, в деяких задачах аналіз об’єднують з побудовою [6, с. 40-45].

Гарним прикладом для зразка загальної схеми розв'язування задачі є така задача:

Побудувати трикутник за двома сторонами і гострому куту, що лежить проти однієї з них рис. 1.2.1.

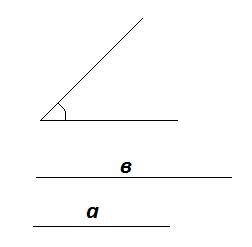
Рис. 1.2.1. Умова до задачі

Розв'язок

Аналіз. Малюємо трикутник А₁В₁С₁, який вважаємо шуканим рис.1.2.2.

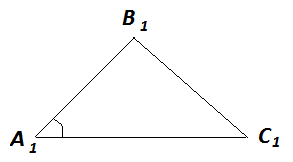
Рис. 1.2.2. Ілюстрація до аналізу

Нехай нам відомі сторони А₁С₁ і В₁С₁ і кут В₁А₁С₁.

А₁С₁=b, В₁С₁=а, кут В₁А₁С₁=α.

Побудувавши сторону А₁С₁, ми визначимо положення двох вершин А₁і С₁, а третя вершина лежить десь на стороні В₁А₁ кута В₁А₁С₁, який ми можемо побудувати. Нам відома ще сторона В₁С₁, отже, третя вершина віддалена від С₁ на В₁С₁, тобто повинна лежати на колі з центром в точці С₁ і радіусом, рівним стороні В₁С₁.

Звідси така побудова.

На довільній прямій МN відкладаємо відрізок АС, рівний b і будуємо кут КАС, рівний даному куту. З центром в точці С описуємо коло радіуса а, рівного другій стороні трикутника. Точка або кожна із точок перетину цього кола з променем АК і буде третьою вершиною шуканого трикутника.

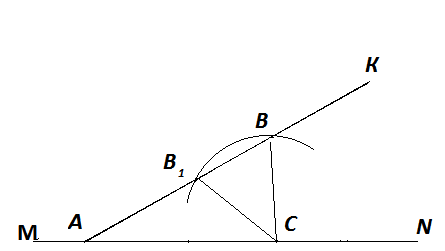
Рис. 1.2.3. Побудова трикутника

Доведення.

Одержані трикутники АВС і АВ₁С – шукані, тому що за побудовою кут ВАС дорівнює куту В, АС = b, і В₁С = ВС = а.

Дослідження.

Так як ми знаходили точки перетину кола з променем АК, то може бути дві точки перетину (задача має 2 розв'язки), одна точка (задача має 1 розв'язок) і жодної точки (задача не має розв'язку).

1.3 Основні геометричні побудови.

Задачі на побудову геометричних фігур на площині відіграють велику роль при вивченні математики. У кожній задачі на побудову фігури треба за даними її елементами знайти інші (шукані) елементи, які перебувають один до одного і до даних елементів у певних співвідношеннях і які можна побудувати за допомогою певних креслярських інструментів. Розв’язати задачу на побудову означає знайти скінченну послідовність елементарних побудов, після виконання яких шукана фігура буде вважатися побудованою на основі прийнятих аксіом конструктивної геометрії.

В ході нашого дослідження було виявлено, що для того щоб побудувати задану фігуру спочатку треба знати основні побудови, які виконуються за допомогою лінійки та циркуля. Нами виявлено 20 основних задач на побудову:

Побудова трикутника з даними сторонами a, b, c.

Розв’язання. За допомогою лінійки проводимо довільну пряму і позначаємо на ній довільну точку В (рис. А. 2). Розхилом циркуля, що дорівнює а, описуємо коло з центром В і радіусом а. Нехай С – точка перетину цього кола з прямою. Тепер розхилом циркуля, що дорівнює с, описуємо коло з центром у точці В, а розхилом циркуля, що дорівнює b, описуємо коло з центром у точці С. Нехай А – точка перетину цих кіл. Проведемо відрізки АВ і АС. Трикутник АВС має сторони, які дорівнюють а, b, с [7, с. 78].

2. Побудова кута, що дорівнює даному.

Розв’язання. Проведемо довільне коло з центром у вершині А даного кута (рис. А. 3). Нехай В і С – точки перетину кола із сторонами кута. Проведемо коло радіусом АВ з центром у точці – початковій точці даної півпрямої (рис. А. 4). Точку перетину цього кола з даною півпрямою позначимо 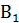, опишемо коло з центром 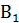і радіусом ВС. Точка 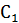перетину побудованих у даній півплощині кіл лежить на стороні шуканого кута. Для доведення досить зазначити, що ΔАВС і Δ 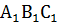рівні як трикутники з відповідно рівними сторонами. ∠А й ∠ є відповідними кутами цих трикутників.

3. Поділ відрізка навпіл.

Розв’язання. Нехай АВ – даний відрізок (рис. А. 5). З точок А і В описуємо кола. Нехай С і 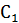– точки перетину цих кіл. Вони лежать у різних півплощинах відносно прямої АВ. Відрізок С 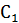перетинає пряму АВ у деякій точці О. Ця точка і є серединою відрізка АВ. Справді, ΔСА 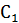і ΔСВ 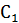рівні за третьою ознакою рівності трикутників. Звідси випливає рівність ∠АСО і ∠ВСО. ΔАСО і ΔВСО рівні за першою ознакою рівності трикутників. Сторони АО і ВО трикутників відповідні й тому рівні. Таким чином. О – середина відрізка АВ.

4. Побудова бісектриси кута даного кута.

Розв’язання. З вершини даного ∠А, як центра, описуємо коло довільного радіуса (рис. А. 6). Нехай В і С – точки перетину цього кола із сторонами кута. З точок В і С таким самим радіусом описуємо кола. Нехай D – точка їх перетину, відмінна від А. Півпряма АD ділить ∠ВАС навпіл. Це впливає з рівності ΔАВD й ΔАСD, у яких кути ∠DAB і ∠DАС відповідні [8, с. 50].

5. Побудова перпендикулярної прямої.

Розв’язання. Можливі два випадки:

1) точка О лежить на прямій а;

2) точка О не лежить на прямій а.

Розглянемо перший випадок (рис. А. 7). З точки О довільним радіусом проводимо коло. Воно перетинає пряму а у двох точках: А і В. З точок А і В проводимо кола радіусом АВ. Нехай С – точка їх перетину. Шукана пряма проходить через точки О й С. Перпендикулярність прямих ОС й АВ випливає з рівності кутів при вершині О ΔАСО і ΔВСО. Ці трикутники рівні за третьою ознакою рівності трикутників.

Розглянемо другий випадок (рис. А. 8). З точки О проводимо коло, що перетинає пряму а. Нехай А і В – точки перетину його з прямою а. З точок А і В таким самим радіусом проводимо кола. Нехай 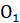– точка їх перетину, що лежить у півплощині, відмінній від тієї, у якій лежить точка О. Шукана пряма проходить через точки О й 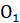. Доведемо це. Позначимо через С точку перетину прямих АВ і О 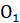. ΔАОВ й ΔА 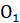В рівні за третьою ознакою рівності трикутників, тому ∠ОАС дорівнює ∠ОА 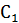. Тоді ΔОАС і Δ 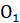АС рівні за першою ознакою рівності трикутників. Отже, ∠АСО й ∠АС 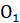рівні. Оскільки ці кути суміжні, то вони прямі. Таким чином, ОС – перпендикуляр, опущений з точки О на пряму а.

6. Побудова паралелограма за даними сторонами a і b і одного з кутів α.

Розв’язання. Будуємо ∠ А= a; на його сторонах відкладаємо відрізки АС = а, АВ = b (рис. А. 9). Проводимо з В дугу mn радіусом а і з С – дугу pq радіусом b. Точку перетину цих дуг D з’єднуємо з С і В.

7. Побудувати квадрат за даною його діагоналлю АВ.

Розв’язання. Через середину АВ (рис. А. 10) проводимо до АВ перпендикуляр MN. Від точки О його перетину з АВ відкладаємо на MN відрізки ОС і OD, що дорівнюють ОА; АВСD – шуканий квадрат.

Не нашли, что искали? Воспользуйтесь поиском: