метод ньютона второго порядка для решения УУН.

Учет нелинейности при моделиро­вании УУН осуществляется через квадратичные члены (слагаемые со вторыми производными) разложения Тейлора (8.22) в виде

(8.34)

Более полный квадратичный учет нелинейности по сравнению с линейным в методе Ньютона способствует значительно лучшей сходимости и уменьшению времени решения уравнений. Поясним это графически (рис. 8.1) на примере нели­нейного уравнения с одной неизвестной ω(U).

По методу Ньютона (метод касательных), заменив в начальной точке U⁽⁰⁾ нелинейное уравнение ω(U) касательной 1 (линейная аппроксимация) и решени­ем линейного уравнения

находится приращение ΔU, и значение переменной . По методу Ньютона второго порядка нелинейное уравнение заменяется кривой второго по­рядка 2 (квадратичная аппроксимация) и решением квадратичного уравнения

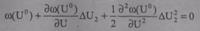(8.34 а)

вычисляется приращение ΔU₂, дающее новое значение переменной , которое значительно ближе к точному решению (корню) U по сравнению с приближе­нием , полученным методом Ньютона.

Рис. 8.1. Линейная (1) и квадратичная (2) аппроксимации нелинейного уравнения ω(U) в точке U⁽⁰⁾.

Приращение ΔU₂, определяемое из решения квадратичного уравнения (8.34 а), назовем приращением второго порядка. Использование его в рекуррентном выра­жении итерационного процесса при определенных условиях обеспечивает более быструю и надежную сходимость.

Возвращаемся к общему (многомерному) случаю. Основная трудность ме­тода второго порядка заключается в решении системы (8.22) квадратичных урав­нений (СКУ)

(8.35)

на каждом шаге вместо СЛУ (8.31)

(8.36)

в методе Ньютона первого порядка.

Существуют различные пути алгоритмической реализации метода второго поряд­ка в зависимости от способа получения приращения ΔU из СКУ (8.35). В связи с тем, что применение прямых методов для этой цели невозможно, учет нелинейности УУН посредством квадратичного разложения осуществляется косвенно и связан с дополни­тельным решением СЛУ в новом итерационном процессе.

Обозначим ΔU, как вектор приращения первого порядка, полученный методом Ньютона при решении СЛУ (8.36). Используя ΔU₁, результирующее при­ращение второго порядка можно определить из решения вспомогательной СЛУ

(8.37)

где D — вектор квадратичных добавок в отрезке ряда Тейлора (8.22).

Таким образом, одна внешняя итерация решения УУН заключается в после­довательном решении СЛУ (8.36) и (8.37).

Применительно к уравнению ω(U) = О с одной неизвестной СЛУ (8.37) можно записать

отсюда приращение второго порядка

(8.38)

с учетом того, что в методе касательных приращение первого порядка , в итоге получим

(8.39)

Другой способ построения итерационной процедуры второго порядка заключается в том [53], что для решения СКУ (8.35) выполняют два шага по методу Ньютона Во-первых, как и в предыдущем случае, определяются поправки ΔU, из решения СЛУ (8.36). Во-вторых, вычисляются невязки СКУ (8.22) в точке U⁽¹⁾ = U⁽⁰⁾ + Δ ,

т. е.

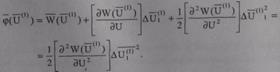(8.39 а)

Заметим, что выражение справедливо для любого (k-го) шага метода после решения СЛУ (8.36).

После корректировки матрицы Якоби:

решается вспомогательная СЛУ:

(8.40)

относительно δU и находится результирующее приращение

(8.41)

Для сравнения с предыдущими способами перепишем СЛУ (8.40) в виде

(8.42)

Для решения уравнения с одной переменной ω(U) = 0 с учетом ΔU₁ =-ω(U)/ω^’(U) и (8.42) результирующее приращение второго порядка опре­деляют по формуле

(8.43)

Отметим, что, хотя объем вычислений по сравнению с методом Ньютона удваи­вается, общее время решения благодаря резкому улучшению сходимости уменьшается существенно (в отдельных случаях до 3-5 раз [53]) при близком расходовании памяти ЭВМ. Дополнительный объем вычисления определяется решением СЛУ (8.37) и до-расчетом вторых производных в едином цикле формирования матриц Якоби и Гессе. Заметим, что квадратичная аппроксимация достаточно точно отражает режим ЭС, а эффективность метода в значительной мере зависит от формы записи УУН. Так, урав­нения баланса мощности в своем изначальном виде являются квадратичными и полно (без остальных членов) описываются анализируемым отрезком разложения ряда Тей­лора (8.22), а потому решения такого уравнения можно получить за одну итерацию. В итоге отметим, что в методе Ньютона второго порядка число внешних итераций

(8.44)

существенно меньше, чем в методе Ньютона. Эффективность метода по времени решения задачи на ЭВМ немаловажна в АСДУ, в проектных и исследовательских задачах, особенно при анализе сильно загруженных ЭС, и возрастает с увеличе­нием размерности задачи, т. е. при расчетах режимов больших и сверхбольших ЭЭС(1—3 тыс. узлов).

Не нашли, что искали? Воспользуйтесь поиском: