Задания для выполнения лабораторной работы №7.

«Операторы языка С++»

Вариант 1. Устаревшая денежная система Великобритании состояла из фунтов, шиллингов и пенсов. Один фунт был равен 20 шиллингам, а один шиллинг – 12 пенсам. Для записи использовалась система, состоящая из знака £ и трёх десятичных значений, разделённых точками. Например, запись £5.2.8 обозначала 5 фунтов, 2 шиллинга и 8 пенсов. Современная денежная система, принятая в 50-е годы XX века, состоит из фунтов и пенсов. Один фунт равен 100 пенсам. Такой фунт называется десятичным. В новой денежной системе указанная сумма обозначается как £5.13 (если быть точнее £5.1333333). Разработайте программу, которая преобразует сумму, записанную в старом формате (фунты, шиллинги, пенсы),в сумму, записанную в новом формате (фунты, пенсы).

Вариант 2. Разработайте программу, изображающую на экране видеомонитора пирамиду из символов ‘X’. Верхняя часть пирамиды должна выглядеть следующим образом:

X

XXX

XXXXX

XXXXXXX

XXXXXXXXX

Пирамида должна быть высотой в 20 линий.

Вариант 3. Напишите программу, рассчитывающую сумму денег, которые вы получите при вложении начальной суммы с фиксированной процентной ставкой дохода через определённое количество лет. Пользователь вводит с клавиатуры начальный вклад, число лет и процентную ставку.

Вариант 4. Напишите программу-эквивалент калькулятора, выполняющего четыре основных арифметических операции. Программа должна запрашивать ввод пользователем первого операнда, знака операции и второго операнда. Для хранения операндов следует использовать переменные вещественного типа. Выбрать операцию можно при помощи оператора switch. В конце программа должна отображать результат на экране. Результат работы программы с пользователем имеет вид:

Введите первый операнд, операцию и второй операнд: 10/3

Результат равен 3,333333

Выполнить ещё одну операцию (y/n)?

Вариант 5. Напишите программу для вычисления положения тела, брошенного под углом к горизонту, в произвольный момент времени t. Учесть сопротивление воздуха: сила трения пропорциональна скорости тела. Начальная скорость тела равна V и направлена под углом α к горизонту. Для вычислений использовать дискретную модель. В векторном виде уравнение имеет вид =m* , где через обозначен коэффициент пропорциональности, входящий в выражение для силы сопротивления воздуха . В проекциях на координатные оси получаем уравнения и . В модели дискретного времени получаем уравнения и

,

где обозначено - коэффициент;

- горизонтальная координата в момент времени ;

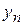- вертикальная координата в момент времени ;

- проекция скорости на горизонтальную ось в момент времени ;

- проекция скорости на вертикальную ось в момент времени ;

- шаг дискретности по времени.

Для сравнения приведём точное решение. Оно имеет вид , .

Вариант 6. Напишите программу для решения квадратного уравнения, которое имеет вид . Параметры a, b и c вводятся пользователем. Использовать аналитические формулы для решений уравнения, при этом учесть различные варианты. Например, , отсутствие решений (комплексные решения).

Вариант 7. Дано натуральное число n . Найти все меньшие n простые числа, используя решето Эратосфена. Решетом Эратосфена называют следующий способ. Выпишем все целые числа от 2 до n. Первое простое число 2. Подчеркнем его, а все большие числа, кратные 2, зачеркнем. Первое из оставшихся чисел 3. Подчеркнем его как простое, а все большие числа, кратные 3, зачеркнем. Первое число из оставшихся теперь 5, т.к. 4 уже зачеркнуто. Подчеркнем его как простое, а все большие числа, кратные 5, зачеркнем и т.д.

Вариант 8. Даны натуральные числа Определить количество членов последовательности являющихся

1. нечетными числами;

2. кратных 3 и не кратных 5;

3. квадратами четных чисел;

4. удовлетворяющих условию ;

5. удовлетворяющих условию ;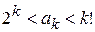

6. имеющих четные порядковые номера и являющихся нечетными числами.

Вариант 9. Написать программу решения по методу Гаусса системы линейных уравнений . Квадратная матрица , , и вектор - исходные данные задачи. Система совместна и имеет единственное решение. Применить программу для решения системы уравнений

Вариант 10. Дано действительное число . Вычислить интеграл с точностью . В данной задаче вычисление с точностью означает следующее. Отрезок интегрирования разбивается на равных частей и строится сумма , которая является приближённым значением интеграла. Если выполняется условие , то считается значением интеграла с точностью . Здесь 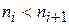i=1,2,…: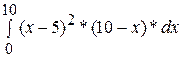

Не нашли, что искали? Воспользуйтесь поиском: