
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
В4 Решения задач диагностической работы
1.1. Первое решение. В прямоугольном треугольнике ABC гипотенуза AB равна 10. Найдем катет BC. Используя теорему Пифагора, имеем BC = 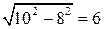 . Следовательно, sin A = 0,6. . Следовательно, sin A = 0,6.
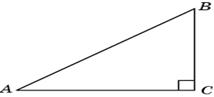 Второе решение. Так как катет AC равен 8, а гипотенуза AB равна 10, то cos A = 0,8. Воспользуемся формулой
Второе решение. Так как катет AC равен 8, а гипотенуза AB равна 10, то cos A = 0,8. Воспользуемся формулой  , выражающей косинус через синус острого угла. Откуда sin A = 0,6.
Ответ. 0,6 , выражающей косинус через синус острого угла. Откуда sin A = 0,6.
Ответ. 0,6
|
1.2. Первое решение. Воспользуемся формулой 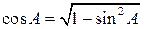 . Тогда cos A = . Тогда cos A =  = 0,8.
Второе решение. Можно считать, что гипотенуза AB и катет BC данного прямоугольного треугольника равны соответственно 10 и 6. Тогда по теореме Пифагора катет AC равен 8 и, следовательно, cos A = 0,8.
Ответ. 0,8. = 0,8.
Второе решение. Можно считать, что гипотенуза AB и катет BC данного прямоугольного треугольника равны соответственно 10 и 6. Тогда по теореме Пифагора катет AC равен 8 и, следовательно, cos A = 0,8.
Ответ. 0,8. 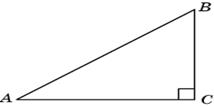
|
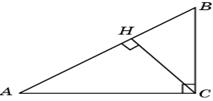
1.3. В прямоугольном треугольнике ACH катет CH равен 6, гипотенуза AC равна 10. Используя теорему Пифагора, находим AH = 8. Следовательно, tg A = 0,75.
Ответ. 0,75.
|
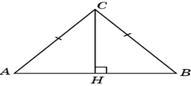
 2.1 Проведем высоту CH. В прямоугольном треугольнике ACH гипотенуза AC равна 10, катет AH равен 6. По теореме Пифагора находим CH = 8 и, следовательно,
sin A = 0,8.
Ответ. 0,8. 2.1 Проведем высоту CH. В прямоугольном треугольнике ACH гипотенуза AC равна 10, катет AH равен 6. По теореме Пифагора находим CH = 8 и, следовательно,
sin A = 0,8.
Ответ. 0,8.
|
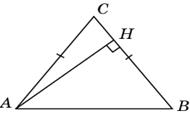
2.2.В прямоугольном треугольнике ABH гипотенуза AB равна 10, катет AH равен 8. По теореме Пифагора находим BH = 6 и, следовательно, cos B = 0,6. Так как углы A и B треугольника ABC равны, то
cos A = 0,6.  Ответ. 0,6.
Ответ. 0,6.
|
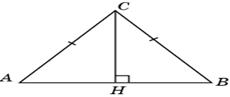 2.3. В прямоугольном треугольнике ACH гипотенуза AC равна 2.3. В прямоугольном треугольнике ACH гипотенуза AC равна  , катет CH равен 8. По теореме Пифагора найдем AH. Имеем AH = , катет CH равен 8. По теореме Пифагора найдем AH. Имеем AH =  = 16. Откуда tg A = 0,5. Так как углы A и C треугольника ABC равны, то тангенс угла ACB равен 0,5.
Ответ. 0,5 = 16. Откуда tg A = 0,5. Так как углы A и C треугольника ABC равны, то тангенс угла ACB равен 0,5.
Ответ. 0,5
|
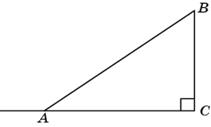 3.1. Синус внешнего угла при вершине A треугольника ABC равен синусу угла A и, следовательно, равен 0,6.
Ответ. 0,6. 3.1. Синус внешнего угла при вершине A треугольника ABC равен синусу угла A и, следовательно, равен 0,6.
Ответ. 0,6.
|
 3.2. Косинус внешнего угла при вершине A равен –cos A. Воспользуемся формулой 3.2. Косинус внешнего угла при вершине A равен –cos A. Воспользуемся формулой 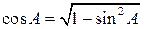 , выражающей косинус острого угла через его синус. Тогда cos A = , выражающей косинус острого угла через его синус. Тогда cos A =  = 0,8 и, следовательно, косинус внешнего угла при вершине A равен –0,8.
Ответ. –0,8. = 0,8 и, следовательно, косинус внешнего угла при вершине A равен –0,8.
Ответ. –0,8.
|
3.3. Тангенс внешнего угла при вершине A равен –tg A. По теореме Пифагора находим BC = 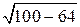 = 6 и, следовательно, tg A = 0,75. Значит, тангенс внешнего угла при вершине A равен –0,75.
Ответ. –0,75. = 6 и, следовательно, tg A = 0,75. Значит, тангенс внешнего угла при вершине A равен –0,75.
Ответ. –0,75.

|
4.1. Первое решение. Рассмотрим прямоугольный треугольник OBC. Его катет BC равен 3, гипотенуза OB равна 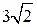 . Следовательно, sin A = . Следовательно, sin A = 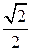 . .
 Второе решение. Угол AOB равен 45о. Следовательно, sin A = Второе решение. Угол AOB равен 45о. Следовательно, sin A = 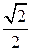 .
Ответ. 2. .
Ответ. 2.
|
4.2. Рассмотрим прямоугольный треугольник OBC. Его катеты BC и OC равны соответственно 4 и 2. Следовательно, тангенс угла BOC равен 2. Учитывая, что тангенс смежного угла равен тангенсу данного угла, взятому с противоположным знаком, получаем, что тангенс угла AOB равен – 2.
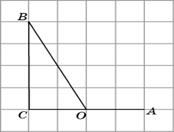 Ответ. – 2. Ответ. – 2.
|
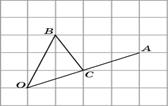 4.3.Рассмотрим треугольник OBС:
OC = BC = 4.3.Рассмотрим треугольник OBС:
OC = BC = 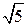 , OB = , OB =  . Следовательно, треугольник OBC – прямоугольный, косинус угла AOB равен . Следовательно, треугольник OBC – прямоугольный, косинус угла AOB равен 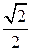 .
Ответ. 2. .
Ответ. 2.
|
5.1.Подставляя в формулу BC = AB 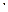 sin A данные значения BC и sin A, находим AB = 5.
Ответ. 5. sin A данные значения BC и sin A, находим AB = 5.
Ответ. 5.

|
5.2.Имеем BC = AC 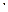 tg A = 8 tg A = 8 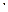 0,75 = 6. По теореме Пифагора находим AB = 0,75 = 6. По теореме Пифагора находим AB = 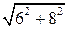 = 10. = 10.
 Ответ. 10. Ответ. 10.
|
 5.3. Углы BCH и BAC равны, как острые углы с перпендикулярными сторонами, значит, cos 5.3. Углы BCH и BAC равны, как острые углы с перпендикулярными сторонами, значит, cos 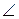 BCH = 0,8. CH = BC BCH = 0,8. CH = BC 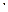 cos cos 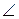 BCH = 4,8.
Ответ. 4,8. BCH = 4,8.
Ответ. 4,8.
|
6.1. Первое решение. Проведем высоту CH. Имеем CH = AC  sin A = 8. По теореме Пифагора находим AH = sin A = 8. По теореме Пифагора находим AH = 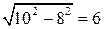 и, следовательно, AB = 12. и, следовательно, AB = 12.
 Второе решение. Проведем высоту CH. Воспользуемся формулой Второе решение. Проведем высоту CH. Воспользуемся формулой 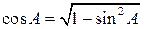 , выражающей косинус острого угла через его синус. Тогда cos A = , выражающей косинус острого угла через его синус. Тогда cos A = 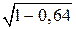 = 0,6. Следовательно, AH = AC = 0,6. Следовательно, AH = AC 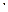 cos A = 6 и, значит, AB = 12.
Ответ. 12. cos A = 6 и, значит, AB = 12.
Ответ. 12.
|
6.2. Первое решение. В равнобедренном треугольнике ABC угол A равен углу B, BH = AB 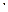 cos B = 6. По теореме Пифагора находим AH = cos B = 6. По теореме Пифагора находим AH =  . .
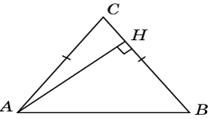 Второе решение. Воспользуемся формулой Второе решение. Воспользуемся формулой  , выражающей синус острого угла через его косинус. Тогда sin A = , выражающей синус острого угла через его косинус. Тогда sin A =  = 0,8. Следовательно, поскольку в равнобедренном треугольнике = 0,8. Следовательно, поскольку в равнобедренном треугольнике 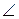 A = A = 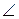 B, получаем AH = AB B, получаем AH = AB  sin B = 8.
Ответ. 8. sin B = 8.
Ответ. 8.
|
6.3. Первое решение. В равнобедренном треугольнике ABC угол A равен углу C,значит, tg A = tg C и AH = 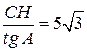 . По теореме Пифагора находим AC = . По теореме Пифагора находим AC = 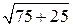 = 10 = 10
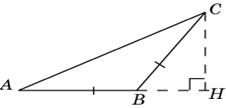 Второе решение. Так как tg C = Второе решение. Так как tg C =  , то угол C равен 30о. Угол A равен углу C. Так как катет прямоугольного треугольника, лежащий против угла в 30о, равен половине гипотенузы, то AC = 10.
Ответ. 10. , то угол C равен 30о. Угол A равен углу C. Так как катет прямоугольного треугольника, лежащий против угла в 30о, равен половине гипотенузы, то AC = 10.
Ответ. 10.
|
Не нашли, что искали? Воспользуйтесь поиском: