Основные формулировки второго закона термодинамики

Второй закон термодинамики формулирует условия взаимных превращений теплоты и работы, не затрагивая вопроса об их количественных соотношениях.

Р. Клаузиус (1850 г.): Теплота не может переходить от холодного тела к более нагретому сама собой, даровым процессом (без компенсации).

В. Томсон (1851 г.): Невозможно при помощи неодушевленного материального двигателя получить от какой-либо массы вещества механическую работу путем охлаждения ее ниже самого холодного из окружающих предметов.

М. Планк: Невозможно построить периодически действующую машину, все действие которой сводилось бы к поднятию некоторого груза и охлаждению теплового источника.

В. Ф. Оствальд: Осуществление вечного двигателя второго рода (который мог бы совершать механическую работу только за счет охлаждения источника теплоты) невозможно.

Рассмотрим систему, в которой теплота q₁, отнимаемая от верхнего источника с температурой Т₁, передается рабочему телу, совершающему обратимый цикл в двигателе А. В результате производится полезная работа l ₀ = q₁ - q₂, передаваемая машине В, а теплота q ₂ сбрасывается в нижний источник.

Общая форма: Если в заданной системе какие-либо процессы могут протекать самопроизвольно, то обратные по отношению к ним процессы возможны лишь при условии определенных компенсирующих изменений состояния системы, а протекать самопроизвольно они не могут.

Иными словами, все самопроизвольные процессы природы необратимы.

Цикл Карно

В цикле, предложенном С. Карно, теплота подводится и отводится по изотермам при температурах горячего источника теплоты и холодного теплоприемника.

Термический к.п.д. прямого цикла Карно

где и

для адиабат 2-3 и 3-4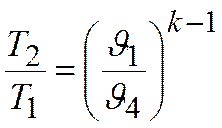

следовательно 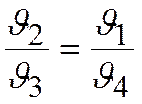и .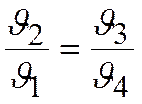

Окончательно или

Термический к.п.д. прямого цикла Карно тем больше, чем выше температура горячего источника теплоты и чем ниже температура холодного теплоприемника.

В обратном цикле Карно холодильный коэффициент

Энтропия

Для прямого цикла Карно вытекает, что

или

Теплота q₂ отводится в цикле, и поэтому отрицательна

или

В каждом элементарном цикле (например, в цикле a–b–c–d–a) теплота подводится на верхнем участке в количестве dq₁ при температуре Т₁ и отводится на нижнем участке в количестве dq₂ при температуре Т₂.

Для каждого из них можно написать:

Взяв линейный интеграл, получаем

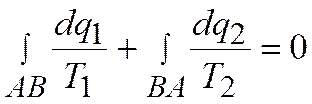или

Если линейный интеграл, взятый по любому замкнутому контуру, равен нулю, то под интегралом находится полный дифференциал, в данном случае:

Если тело переходит из состояния 1 в состояние 2, то по какому бы пути не был осуществлен переход, величина

будет иметь одно и то же значение.

Функция состояния S названа Клаузиусом энтропией.

Изменение энтропии в любом обратимом процессе является признаком наличия теплообмена между рабочим телом и окружающей средой.

Энтропию можно рассматривать как параметр состояния и, следовательно, изменение ее можно вычислить для любого процесса, если известно изменение двух других параметров состояния.

Дифференцируя уравнение состояния идеального газа, получаем

Разделив левую часть уравнения на рJ, а правую на RT, получаем

или

Если в качестве независимых переменных заданы J и Т:

На основании первого закона термодинамики

поскольку

получаем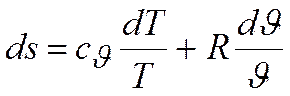

Интегрируя, получим

Если в качестве независимых переменных заданы р и Т:

,

получаем ,

или, поскольку с_J+R = с_р, имеем .

Интегрируя:

Если в качестве независимых переменных заданы J и р:

получаем 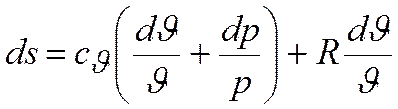или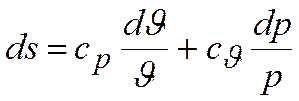

Интегрируя:

Начало отсчета энтропии – нормальные условия р_о = 760 мм.рт.ст и t_о = 0⁰С. Тогда при любых других условиях, заданных параметрами р и Т, значение энтропии можно определить:

Очевидно, что при одинаковых температурах теплоотдатчика и теплоприёмника термический КПД цикла с наличием необратимых процессов будет ниже, чем в полностью обратимом цикле:

или

Но для прямого обратимого цикла термический КПД можно выразить через температуры (см. раздел 3.2):

Отсюда, , или .

Как известно, алгебраическая сумма приведённых теплот для произвольного цикла равна нулю:

Теплота 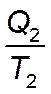имеет отрицательный знак, т.к. она отводится в цикле, поэтому:

, и, следовательно, при наличии в цикле необратимых процессов (для необратимых циклов в целом):

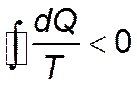
Ранее было получено выражение изменения энтропии в процессе:

В обратимом адиабатном процессе , а значит .

Определим, как изменяется энтропия в необратимых процессах.

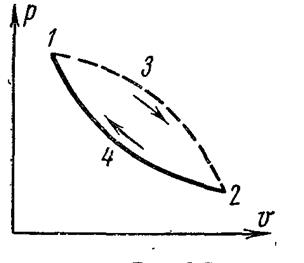Между состояниями 1 и 2 осуществляется необратимый процесс. Обратимый процесс между этими состояниями показан линией 2-4-1. Таким образом, имеем необратимый цикл.

Для такого цикла справедливо записать 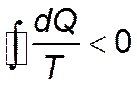(получено ранее), или

Для обратимого цикла , т.е. , а для элементарного необратимого процесса

Значит, в необратимых процессах энтропия увеличивается.

Не нашли, что искали? Воспользуйтесь поиском: