If n < 6 then begin

Begin

writeln(n);

if n <= 5 then begin

F(n + 2);

F(n + 3)

End

end;

Найдите сумму чисел, которые будут выведены при вызове F(2).

Решение (вариант 1, построение дерева вызовов):

1) поскольку в начале каждого вызова на экран выводится значение единственного параметра функции, достаточно определить порядок рекурсивных вызовов и сложить значения параметров

2) поскольку при 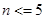выполняется два рекурсивных вызова, решать такую задачу «на бумажке» удобно в виде двоичного дерева (в узлах записаны значения параметров при вызове функции):

3) складывая все эти числа, получаем 39

Ответ: 39.

Решение (вариант 2, подстановка):

1) можно обойтись и без дерева, сначала определим рекуррентную формулу; сумму чисел, полученных при вызове , обозначим через :

2) при n >5 процедура выводит число n и заканчивает работу без рекурсивных вызовов:

S(n) = n, при n >5

3) при n <=5 процедура выводит число n и вызывает следующие процедуры:

S(n) = n + S(n+2) + S(n+3) при n <=5

4) выполняем вычисления:

5) теперь остаётся вычислить ответ «обратным ходом», подставив значения в предыдущее выражение:

Ответ: 39.

ЕЩЕ ПРИМЕР

Дан рекурсивный алгоритм:

procedure F(n: integer);

Begin

writeln(n);

if n < 6 then begin

F(n+2);

F(n*3)

End

end;

Найдите сумму чисел, которые будут выведены при вызове F(1).

Решение (вариант 1, метод подстановки):

1) сначала определим рекуррентную формулу; обозначим через G(n) сумму чисел, которая выводится при вызове F(n)

2) при n >= 6 процедура выводит число n и заканчивает работу без рекурсивных вызовов:

G(n) = n, при n >= 6

3) при n < 6 процедура выводит число n и дважды вызывает сама себя:

G(n) = n + G(n+2) + G(3n) при n < 6

4) в результате вызова F(1) получаем

G(1) = 1 + G(3) + G(3)

G(3) = 3 + G(5) + G(9) = 3 + G(5) + 9

G(5) = 5 + G(7) + G(15) = 5 + 7 + 15 = 27

5) используем обратную подстановку:

G(3) = 3 + G(5) + 9 = 3 + 27 + 9 = 39

G(1) = 1 + 2*G(3) = 79

6) Ответ: 79.

Не нашли, что искали? Воспользуйтесь поиском: