
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Практическая работа 5. Применение системы компьютерной алгебры Maxima к расчету и анализу процессов теплообмена
5.1 Система компьютерной алгебры Maxima
Рассмотрим различные команды в Maxima. Любая команда завершается знаком «;». Чтобы выполнить команду, необходимо нажать сочетание клавиш «Shift+Enter». После выполнения команды она сама и ее результат отмечаются символами (%i1) и (%o1), означающими ввод (input) и вывод (output). Все команды нумеруются.
Простые арифметические операции выполняются следующим образом:
(%i1) 2+2;
(%o1) 4
(%i2) 2+2*2;
(%o2) 6
(%i3) 5!;
(%o3) 120
Для выполнения действий над результатом предыдущей команды используется ссылка на него в виде %:
(%i1) 2+2;
(%o1) 4
(%i2) %+3;
(%o2) 5
Maxima поддерживает работу с выражениями в символьном виде:
(%i1) x^2+3;
(%o1) x2+3
(%i2) %+2*x^2;
(%o2) 3x2+3
Упрощение выражений в Maxima выполняется по умолчанию. Когда это необходимо отметить особо, используют команду ratsimp (рис. 5.1):

Рис. 5.1. Пример применения команды ratsimp
Для решения простых уравнений и их систем используется команда solve (рис. 5.2):

Рис. 5.2. Пример применения команды solve
Для вывода графиков может быть использована команда plot2d. Для ее использования необходимо указать функцию и пределы построения графика по осям. Например, plot2d(sin(x),[x,0,10]); дает результат, представленный на рис. 5.3.

Рис. 5.3. Пример применения команды plot2d
Для вывода на график дискретных значений используется опция discrete в команде plot2d. Например, plot2d([discrete, [0,1,2,3,4], [20,10,8,11]]); дает результат, представленный на рис. 5.4.

Рис. 5.4. Пример применения команды plot2d для дискретных значений
5.2 Расчет теплопередачи через многослойную стенку
Рассмотрим следующую задачу расчета теплопередачи через многослойную стенку (рис. 5.5). Пусть с одной стороны многослойной стенки имеется тепловой поток q. Стенка состоит из трех слоев, каждый из которых имеет характеристики толщины δ и теплопроводности λ. На границах слоев стенки выделим характерные точки, в которых будем контролировать температуры t1..t4. С другой стороны стенка имеет конвективный теплообмен с окружающей средой с температурой t5.

Рис. 5.5. Расчетная схема задачи
Для решения задачи теплопередачи через многослойную стенку запишем основные уравнения. Каждое из первых трех уравнений характеризует тепловой поток, идущий через один слой стенки. Последнее уравнение характеризует тепловой поток, отданный от стенки в окружающую среду.
 (5.1)
(5.1)
В этих уравнениях λ – теплопроводность материала стенки, δ – толщина стенки, q– удельный тепловой поток, α – коэффициент конвективной теплоотдачи, t– температура в конкретной точке системы, 1..4 – характерные сечения на границах стенок.
Рассмотрим задачу в следующей постановке: известны все теплофизические свойства слоев и их толщина, коэффициент теплоотдачи. Необходимо определить распределение температур по толщине стенки. Для решения такой задачи надо задать два граничных условия: величину удельного теплового потока qи температуру окружающей среды t5.
В качестве исходных примем данные из таблицы 5.1.
Таблица 5.1. Исходные данные для задачи
| Параметр | Значение |
| q | 1000 Вт/м2 |
| δ1 | 10 мм = 0,01 м |
| δ2 | 20 мм = 0,02 м |
| δ3 | 30 мм = 0,03 м |
| λ1 | 300 Вт/(м*С) |
| λ 2 | 200 Вт/(м*С) |
| λ 3 | 100 Вт/(м*С) |
| t5 | 20 С |
| α | 500 Вт/(м2*С) |
В результате получится система уравнений:
 (5.2)
(5.2)
Решение системы в Maxima представлено на рис. 5.6.

Рис. 5.6. Решение системы уравнений в Maxima
По умолчанию Maxima проводит вычисления с дробями. Поэтому и решение представленной системы (%o7) представлено в виде дробей. Для того, чтобы получить результат в формате чисел с плавающей точкой, была использована команда float(в меню «Численные расчеты» - «Tofloat»).
Построим график распределения температур по толщине стенки. К сожалению, напрямую обратиться к значению t1..t4 мы не сможем – эти обозначения действительны только в пределах уравнений eq1..eq4. Для построения графика значения температур придется переписывать в функцию вручную. Толщины слоев стенки зададим в миллиметрах. Общая толщина стенки 60 мм (10 мм + 20 мм + 30 мм). В результате получим команду:
plot2d([discrete, [0,10,30,60], [22.43,22.40,22.3,t1]]);
Распределение температур по толщине стенки представлено на рис. 5.7.
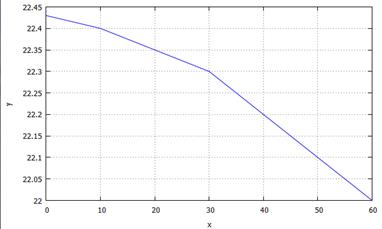
Рис. 5.7. Распределение температур по толщине стенки
5.3 Задание
Для заданного варианта из таблицы 5.2:
- определить температуры на границах слоев,
- построить график распределения температур по толщине стенки,
- исследовать зависимость изменения профиля температуры от изменения исходных данных,
- определить, какой из слоев обладает наибольшим/наименьшим термическим сопротивлением.
Теплопроводность материалов брать из таблицы 5.3.
Таблица 5.2. Задание для практической работы 5
| № | Первая стенка | Вторая стенка | Третья стенка | Удельный поток q, Вт/м2 | Коэффициент теплоотдачи α, Вт/(м2*С) |
| алюминий 3 мм | медь 10 мм | пенополиуретан 30 мм | |||
| медь 2 мм | мрамор 5 мм | стекло 10 мм | |||
| гипсокартон 100 мм | стекло 30 мм | бетон 50 мм | |||
| бетон 20 мм | сталь 5 мм | медь 10 мм | |||
| сталь 50 мм | медь 50 мм | алюминий 70 мм | |||
| гранит 100 мм | бетон 100 мм | пенополиуретан 100 мм | |||
| мрамор 100 мм | стекло 20 мм | алюминий 30 мм | |||
| медь 8 мм | мрамор 2 мм | стекло 2 мм | |||
| песок 10 мм | бетон 10 мм | мрамор 10 мм | |||
| гранит 100 мм | бетон 100 мм | пенополиуретан 1 мм | |||
| гранит 20 мм | стекло 20 мм | песок 20 мм | |||
| пенополиуретан 30 мм | песок 30 мм | бетон 30 мм | |||
| бетон 70 мм | песок 70 мм | мрамор 70 мм | |||
| медь 100 мм | сталь 100 мм | алюминий 100 мм | |||
| пенополиуретан 3 мм | медь 100 мм | алюминий 100 мм | |||
| алюминий 2 мм | стекло 5 мм | мрамор 10 мм | |||
| гипсокартон 100 мм | сталь 2 мм | бетон 150 мм | |||
| бетон 200 мм | сталь 1 мм | медь 1 мм |
Таблица 5.3. Теплопроводность материалов
| Материал | Теплопроводность, Вт/(м*С) |
| Бетон | 1.51 |
| Пенополиуретан | 0.041 |
| Гипсокартон | 0.15 |
| Гранит | 3.49 |
| Мрамор | 2.91 |
| Песок | 0.35 |
| Сталь | |
| Алюминий | |
| Медь | |
| Стекло | 0.76 |
Контрольные вопросы:
1. Решение алгебраических уравнений в Maxima.
2. Построение графиков в Maxima.
3. Постановка задачи теплопередачи через многослойную стенку.
4. Основные уравнения для расчета теплопередачи через многослойную стенку.
5. Порядок расчета теплопередачи через многослойную стенку с использованием Maxima.
| <== предыдущая лекция | | | следующая лекция ==> |
| О ПРОХОЖДЕНИИ СЛУЖБЫ В ОРГАНАХ ВНУТРЕННИХ ДЕЛ РЕСПУБЛИКИ БЕЛАРУСЬ 5 страница | | | Практическая работа по теме «Внешняя политика при Николае I»Ч.1 ПО §12 |
Не нашли, что искали? Воспользуйтесь поиском: