ТОР 5 статей:

Методические подходы к анализу финансового состояния предприятия

Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века

Ценовые и неценовые факторы

Характеристика шлифовальных кругов и ее маркировка

Служебные части речи. Предлог. Союз. Частицы

КАТЕГОРИИ:

Поворот осей координат

⇐ Предыдущая 12

рис. 7.

Під поворотом осей координат розуміють таке перетворення координат, при якому обидві осі повертаються на один і той же кут, а початок координат і масштаб залишаються незмінними.

Нехай нова система 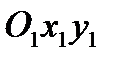отримана поворотом системи Оху на кут .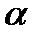

Нехай М — довільна точка площини, (х; у) — її координати в старій системі і (х';у') — в новій системі.

Введемо дві полярні системи координат із загальним полюсом О і полярними осями Ох і Оx₁ (масштаб однаковий). Полярний радіус в обох системах однаковий, а полярні кути відповідно рівні і, де — полярний кут в новій полярній системі.

По формулах переходу від полярних координат до прямокутних маємо

тобто

Але 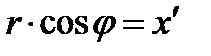. Тому

Отримані формули називаються формулами повороту осей. Вони дозволяють визначати старі координати (х; у) довільної точки М через нові координати (х'; у') цієї ж точки М, і навпаки.

рис. 8.

Якщо нова система координат 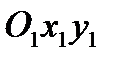отримана із старої Оху шляхом паралельного перенесення осей координат і подальшим поворотом осей на кут 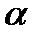(див. рис. 8), то шляхом введення допоміжної системи 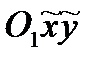легко отримати формули

виражаючи старі координати х і у довільної точки через її нові координати х' і у'.

Тема 3.2. Лінії на площині.

3.2.1. Основні поняття.

Лінія на площині розглядається (задається) як множинаточок,що має певні і притаманні тільки їм геометричні властивості. Наприклад, коло радіусом R це множина всіх точок площини, віддалених на відстань R від деякої фіксованої точки О (центра кола).

Введення на площині системи координат дозволяє визначати положення точки площини завданням двох чисел — її координат, а положення лінії на площині визначається за допомогою рівняння (тобто рівність, що зв'язує координати точок лінії).

Рівняння лінії (або кривої) на площині Оху називається таке рівняння F(х;у)=0 з двома змінними, якому задовольняють координати х і у кожної точки лінії і не задовольняють координати будь-якої точки, які не лежать на цій лінії.

Змінні x і у в рівнянні лінії називаються поточними координатами точок лінії.

Рівняння лінії дозволяє вивчення геометричних властивостей лінії замінити дослідженням його рівняння.

Так, для того, щоб встановити чи лежить точка A(x₀; y₀) на даній лінії, досить перевірити (не вдаючись до геометричних побудов), чи задовольняють координати точки А рівнянню цієї лінії у вибраній системі координат.

Приклад 2.1.: Чи лежать точки К(—2; 1) і L(1; 1) на лінії ?

○ Підставивши в рівняння замість x і у координати точки К, отримаємо . Отже, точки К лежить на даній лінії. Точка L не лежить на даній лінії, оскільки .●

Завдання про знаходження точок перетину двох ліній, заданих рівняннями F₁(х; у)=0 і F₂(х; у)=0, зводиться до відшукування точок, координати яких задовольняють рівняння обох ліній, тобто зводиться до розв’язку системи двох рівнянь з двома невідомими:

Якщо ця система не має дійсних розв’язок, то лінії не перетинаються.

Аналогічним чином вводиться поняття рівняння лінії в полярній системі координат.

Рівняння F(; )=0 називається рівнянням даної лінії в полярній системі координат, якщо координати будь-якої точки, лежать на цій лінії, і лише вони, задовольняють це рівняння. Лінію на площині можна задати за допомогою двох рівнянь:

(2.1)

де х і у — координати довільної точки М(х; у), які лежать на даній лінії, а t — змінна, називається параметром; параметр t визначає положення точки (х; у) на площині.

Наприклад, якщо , у, то значенню параметра відповідає на площині точка з координатами (3; 4), оскільки , .

Якщо параметр t змінюється, то точка на площині переміщається, описуючи дану лінію. Такий спосіб завдання прямої називається параметричним, а рівняння (2.1) — параметричними рівняннями лінії.

Щоб перейти від параметричних рівнянь лінії до рівняння виду F(х;у)=0, треба яким-небудь чином з двох рівнянь виключити параметр t. Наприклад, від параметричних рівнянь 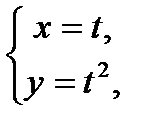шляхом підстановки 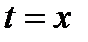в друге рівняння, легко отримати рівняння або , тобто виду F(х; у)= 0. Проте, відмітимо, такий перехід не завжди доцільний і не завжди можливий.

рис. 9.

Лінію на площині можна задати векторним рівнянням, де t — скалярний змінний параметр. Кожному значенню t₀ відповідає певний вектор 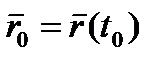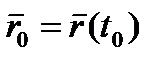площини. При зміні параметра t кінець вектора опише деяку лінію (див. рис. 9).

Векторному рівнянню лінії в системі координат Оху відповідають два скалярні рівняння (2.1), тобто рівняння проекцій на осі координат векторного рівняння лінії є її параметричні рівняння.

Векторне рівняння і параметричне рівняння лінії мають механічний сенс. Якщо точка переміщається на площині, то вказані рівняння називаються рівняннями руху, а пряма — траєкторією точки, параметр t при цьому є час.

Отже, всякій лінії на площині відповідає деяке рівняння виду F(х; у)= 0.

Всякому рівнянню виду F(х; у)= 0 відповідає, взагалі кажучи, деяка лінія, властивості якої визначаються даним рівнянням (вираз «взагалі кажучи» означає, що сказане допускає виключення. Так, рівнянню (х-2)²+(у-3)²=0 відповідає не лінія, а точка (2;3); рівнянню на площині не відповідає ніякий геометричний образ).

У аналітичній геометрії на площині виникають два основні завдання. Перше: знаючи геометричні властивості кривої, знайти її рівняння; друге: знаючи рівняння кривої, вивчити її форму і властивості. На малюнках 10-18 приведені приклади деяких кривих і вказані їх рівняння.

або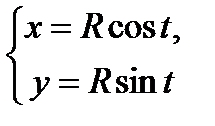

рис. 10. Коло радіусом R

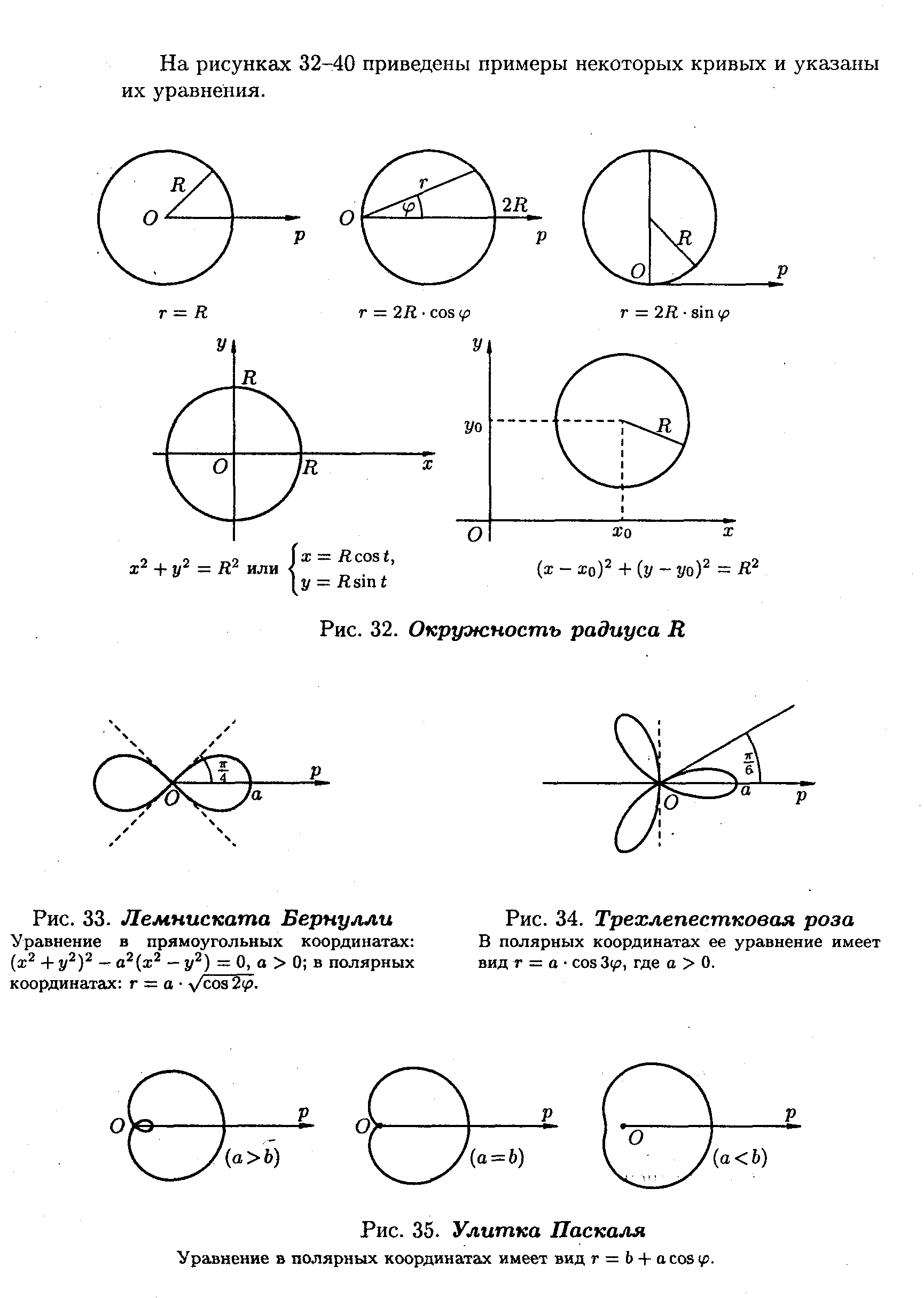
рис. 11. Лемніската Бернуллі рис. 12. Трьохпелюсткова роза
Рівняння в прямокутних координатах: У полярних координатах її рівняння
(х²+у²)²– 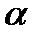²(х²–у²)=0, 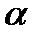> 0; має вигляд, де >0.

у полярних координатах: .

рис. 13. Равлик Паскаля

Рівняння в полярних координатах має вигляд .

рис. 14. Напівкубічна парабола рис. 15. Астроїда

Рівняння кривої у² = х³ або Рівняння в прямокутних координатах: ; параметричні рівняння:

рис. 16. Кардіоїда рис. 17. Спіраль Архімеда

Рівняння в полярних координатах рівняння кривої в полярних

має вигляд , координатах,

де . Кардіоїда — окремий випадок де - постійне.

равлика Паскаля ().

рис. 18. Циклоїда

Параметричні рівняння циклоїди мають вигляд де а > 0.

Циклоїда — це крива, яку описує фіксована точка кола, що котиться без ковзання по нерухомій прямій.

3.2.2. Рівняння прямої на площині.

Найпростішою з ліній є пряма. Різним способам завданням прямої відповідають в прямокутній системі координат різні види її рівнянь.

Рівняння прямої з кутовим коефіцієнтом

Нехай на площині Оху задана довільна пряма, не паралельна осі Оу. Її положення цілком визначається ординатою b точки N(0; b) перетину з віссю Оу і кутом а між віссю Ох і прямій (див. рис. 19).

Під кутом нахилу прямої розуміється найменший кут, на який потрібно повернути навколо точки перетину прямої і осі Ох проти годинникової стрілки вісь Ох до її збігу з прямій.

рис. 19.

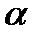Візьмемо на прямій довільну точку М(х;у) (див. рис. 19). Проведемо через точку N вісь , паралельну осі Ох і однаково з нею направлену. Кут між віссю і прямою рівний . У системі точка М має координати х і у - b. З визначення тангенса кута виходить рівність , тобто. .Введенопозначення , отримуємо рівняння

(2.2)

яке задовольняє координати будь-якої точки М(х;у) прямої. Можна переконатися, що координати будь-якої точки Р(х;у), лежить поза даною прямою, рівнянню (2.2) не задовольняють.

Число , називається кутовим коефіцієнтом прямої, а рівняння (2.2) - рівнянням прямої з кутовим коефіцієнтом.

Якщо пряма проходить через початок координат, то і, отже, рівняння цієї прямої матиме вигляд .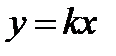

Якщо пряма паралельна осі Ох, то , отже, і рівняння (2.2) прийме вигляд

.

Якщо пряма паралельна осі Оу, то, рівняння (2.2) втрачає сенс, оскільки для неї кутовий коефіцієнт не існує.

В цьому випадку рівняння прямої матиме вигляд

(2.3)

де а - абсциса точки перетину прямої з віссю Ох. Відзначимо, що рівняння (2.2) і (2.3) є рівняння першого ступеня.

Загальне рівняння прямої

Розглянемо рівняння першого ступеня відносно х і у в загальному вигляді

(2.4)

де A, В, С - довільні числа, причому А і В не рівні нулю одночасно.

Покажемо, що рівняння (2.4) є рівняння прямої лінії. Можливі два випадки.

Якщо , то рівняння (2.4) має вигляд 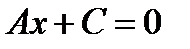, причому , тобто . Це є рівняння прямої, паралельної осі Оу і що проходить через точку .

Якщо , то з рівняння (2.4) отримуємо 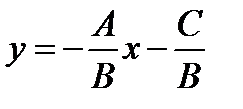. Це є рівняння прямої з кутовим коефіцієнтом .

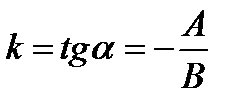Отже, рівняння (2.4) є рівняння прямої лінії, воно називається загальним рівнянням прямої.

Деякі окремі випадки загального рівняння прямої:

1) якщо , то рівняння приводиться до вигляду . Це є рівняння прямої, паралельною осі Ох;

2) якщо , то пряма паралельна осі Oy;

3) якщо , то отримуємо . Рівнянню задовольняють координати точки O(0;0), пряма проходить через початок координат.

Рівняння прямої, що проходить через дану точку в даному напрямі

Нехай пряма проходить через точки і її напрям характеризується кутовим коефіцієнтом k. Рівняння цієї прямої можна записати у вигляді у=kx+b, де b — поки невідома величина. Оскільки пряма проходить через точку 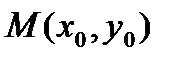, то координати точки задовольняють рівнянню прямої: . Звідси . Підставляючи значення b в рівняння , отримаємо шукане рівняння прямої , тобто

(2.5)

Рівняння (2.5) з різними значеннями k називають також рівняннями пучка прямих з центром в точці 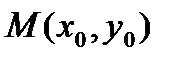. З цього пучка не можна визначити лише пряму, паралельну осі Оу.

Рівняння прямої, що проходить через дві точки

Нехай пряма проходить через точки і . Рівняння прямої, що проходить через точку має вигляд

(2.6)

де k — поки невідомий коефіцієнт.

Оскільки пряма проходить через точку , то координати цієї точки повинні задовольняти рівнянню (2.6): 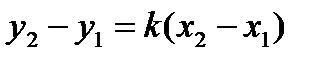.Звідси знаходимо . Підставляючи знайдене значення k в рівняння (2.6), отримаємо рівняння прямої, що проходить через точки М₁ і М₂:

(2.7)

Передбачається, що в цьому рівнянні .

Якщо x₂=x₁, то пряма, що проходить через точки 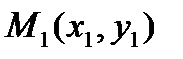і 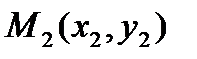, паралельна осі ординат. Її рівняння має вид х = х₁.

Якщо у₂ = у₁, то рівняння прямої може бути записане у вигляді у = у₁, пряма М₁М₂ паралельна осі абсцис.

Рівняння прямої у відрізках

Нехай пряма перетинає вісь Ох в точці М₁(а; 0), а вісь Оу — в точці М₂(0; b) (див. рис. 20). В цьому випадку рівняння (2.7) прийме вигляд

тобто.

рис. 20.

Це рівняння називається рівнянням прямої у відрізках, оскільки числа а і b показують, які відрізки відсікає пряма на осях координат.

Рівняння прямої, що проходить через дану точку перпендикулярно даному вектору

Знайдемо рівняння прямої, що проходить через задану точку М₀(x₀; y₀) перпендикулярно даному ненульовому вектору .

Візьмемо на прямій довільну точку M(x; у) і розглянемо вектор =(x–x₀;у–y₀), (див. рис. 21). Оскільки вектори і перпендикулярні, то їх скалярний добуток рівний нулю: , тобто

(2.8)

рис. 21.

Рівняння (2.8) називається рівнянням прямої, що проходить через задану точку перпендикулярно заданому вектору.

Вектор , перпендикулярний прямій, називається нормальним вектором цієї прямої. Рівняння (2.8) можна переписати у вигляді

(2.9)

де А і В — координати нормального вектора, - вільний член. Рівняння (2.9) є загальне рівняння прямої (див. (2.4)).

Полярне рівняння прямої

Знайдемо рівняння прямої в полярних координатах. Її положення можна визначити, вказавши відстань р від полюса О до даної прямої і кут а між полярною віссю ОР і віссю l, що проходить через полюс О перпендикулярно дану пряму (див. рис. 22).

рис. 22.

Для будь-якої точки на даній прямій маємо:

.

З іншого боку,

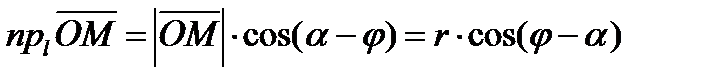
Отже

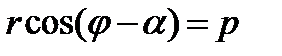. (2.10)

Отримане рівняння (2.10) і є рівняння прямої в полярних координатах.

Нормальне рівняння прямої

Нехай пряма визначається заданням р і а (див. рис. 23). Розглянемо прямокутну систему координат Оху. Введемо полярну систему, взявши О за полюс і Ох за полярну вісь. Рівняння прямої можна записати у вигляді

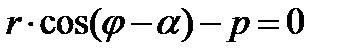тобто

рис. 23.

Але, через формули, що зв'язують прямокутні і полярні координати, маємо: 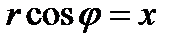, . Отже, рівняння (2.10) прямої в прямокутній системі координат прийме вигляд

. (2.11)

Рівняння (2.11) називається нормальним рівнянням прямої.

Покажемо, як привести рівняння (2.4) прямої до вигляду (2.11).

Помножимо всі члени рівняння (2.4) на деякий множник . Отримаємо . Це рівняння повинне звернутися в рівняння (2.11). Отже, повинна виконуватися рівність: , , 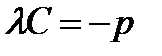. З першої двох рівності знаходимо, тобто Множник 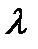називається нормуючим множником. Згіднотретьої рівності знак нормуючого множника протилежний знаку вільного члена із загального рівняння прямої.

Приклад 2.2. Привести рівняння –3x + 4у + 15 = 0 до нормального вигляду.

○ Знаходимо нормуючий множник . Помноживши дане рівняння на, отримаємо шукане нормальне рівняння прямої: .●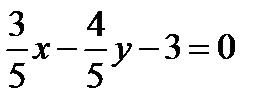

3.2.3. Пряма лінія на площині. Основні задачі.

Кут між двома прямими і умови паралельності і перпендикулярності двох прямих

Нехай прямі L₁ і L₂ задані рівняннями з кутовими коефіцієнтами 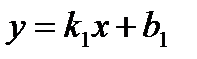і (див. рис. 24).

Потрібно знайти кут, на який треба повернути в позитивному напрямі пряму L1 навколо точки їх перетину до збігу з прямій L2.

○ Маємо 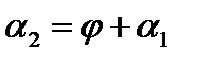(теорема про зовнішній кут трикутника) або .

рис. 24.

Якщо , то

.

Але , , тому

, (2.12)

звідки легко отримаємо величину шуканого кута.

Якщо потрібно обчислити гострий кут між прямими, не враховуючи, яка пряма є першою, яка — другою, то права частина формули (2.12) береться по модулю, тобто .

Якщо прямі L₁ і L₂ паралельні, то і . З формули (2.12) виходить 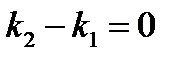, тобто . і навпаки, якщо прямі L₁ і L₂ такі, що , то прямі паралельні. Отже, умовою паралельності два прямих є рівність їх кутових коефіцієнтів: .

Якщо прямі L₁ і L₂ перпендикулярні, то . Отже . Звідси, тобто (або) 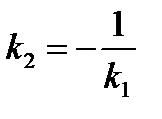. Справедливо і зворотне твердження. Таким чином, умовою перпендикулярності прямих є рівність.●

Відстань від точки до прямої

Нехай задана пряма L рівнянням і точка M₀(x₀;y₀) (див. рис. 25). Потрібно знайти відстань від точки М₀ до прямій L.

рис. 25.

Розв’язок: Відстань d, від точки М₀ до прямою L рівно модулю проекції вектора , де M₁(x₁;y₁) - довільна точка прямої L, на напрям нормального вектора . Отже

.

Оскільки точка M₁(x₁;y₁) належить прямою L, то, тобто . Тому

(2.13)

що і потрібно було отримати.

Приклад 2.3. Знайти відстань від точки M₀(2;-1) до прямій .

○ По формулі (2.13) отримуємо .●

Тема 3.3. Лінії другого порядку на площині.

3.3.1. Основні поняття

Розглянемо лінії, визначувані рівняннями другого порядку відносно поточних координат

Ах²+2Вху+Су²+2Dх+2Еу+F=0. (3.1)

Коефіцієнти рівняння — дійсні числа, але принаймні одне з чисел А, В або С відмінне від нуля. Такі лінії називаються лініями (кривими) другого порядку. Нижче буде встановлено, що рівняння (3.1) визначає на площині коло, еліпс, гіперболу або параболу. Перш, ніж переходити до цього твердження, вивчимо властивості перерахованих кривих.

Коло

Простою кривою другого порядку є коло. Нагадаємо, що колом радіусу R з центром в точці М₀ називається множина всіх точок М площині, які задовольняють умову М₀М=R. Нех ай точка М₀ в прямокутній системі координат Оху має координати х₀,у₀, а М(х; у) — довільна точка кола (див. рис. 26).

Тоді з умови М₀М=R отримуємо рівняння

,

рис. 26.

тобто

(x-x₀)²+(у-y₀)²=R² (3.2)

Рівняння (3.2) задовольняють координати будь-якої точки М(х; у) даного кола і не задовольняють координати ніякої точки, які лежать на колі.

Рівняння (3.2) називається канонічним рівнянням кола.

Зокрема, вважаючи х₀= 0 і у₀= 0, отримаємо рівняння кола з центром на початку координат x₂ + у₂ = R².

Рівняння кола (3.2) після нескладних перетворень прийме вигляд . При порівнянні цього рівняння із загальним рівнянням (11.1) кривої другого порядку легко відмітити, що для рівняння кола виконано дві умови:

1) коефіцієнти біля х₂ і у₂ рівні між собою;

2) відсутній член, що містить добуток ху поточних координат.

Розглянемо зворотне завдання. Поклавши в рівнянні (3.1) значення і, отримаємо

. (3.3)

Перетворимо це рівняння:

,

Тобто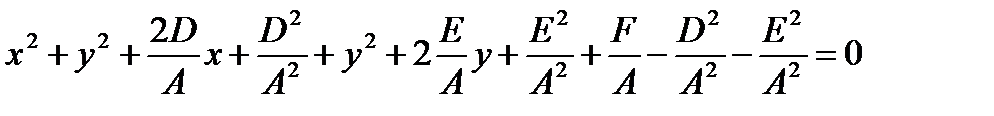

т. е. . (3.4)

Звідси витікає, що рівняння (3.3) визначає коло за умови 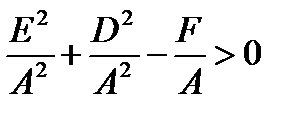. Її центр знаходиться в точці , а радіус .

Якщо ж, то рівняння (3.3) має вигляд

.

Йому задовольняють координати єдиної точки . В цьому випадку говорять: «коло виродилося в точку» (має нульовий радіус).

Якщо , то рівняння (3.4), а отже, і рівносильне рівняння (3.3), не визначає ніякої лінії, оскільки права частина рівняння (3.4) негативна, а ліва частина — не негативна (говорять: «коло уявне»).

3.3.3. Еліпс

Канонічне рівняння еліпса

Еліпсом називається множина всіх точок площини, сума відстаней від кожної з яких до двох заданих точок площини, які називаються фокусами, є величина постійна, більша, ніж відстань між фокусами.

Позначимо фокуси через F₁ і F₂, відстань між ними через 2с, а суму відстаней від довільної точки еліпса до фокусів — через 2а (див. мал. 49). За визначенням 2a>2с, тобто .

рис. 27.

Для виведення рівняння еліпса виберемо систему координат Оху так, щоб фокуси F₁ і F₂ лежали на осі Ох, а початок координат співпадав з серединою відрізка F₁F₂. Тоді фокуси матимуть наступні координати:

F₁(-с; 0) і F₂(с; 0).

Нехай М(х;у) — довільна точка еліпса. Тоді, згідно визначенню еліпса,

МF₁ + МF₂=2а, тобто

(3.5)

Це, по суті, і є рівняння еліпса.

Перетворимо рівняння (3.5) до простішого вигляду таким чином:

,

,

,

,

.

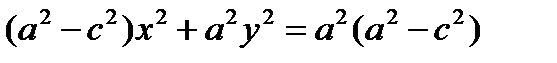Оскільки а > с, то а² - с² > 0. Покладемо

a² – c² = b² (3.6)

Тоді останнє рівняння прийме вид b²х² + а²у² = а²b² або

(3.7)

Можна довести, що рівняння (3.7) рівносильне початковому рівнянню. Воно називається канонічним рівнянням еліпса. Еліпс — крива другого порядку.

Дослідження форми еліпса по його рівнянню

Встановимо форму еліпса, користуючись його канонічним рівнянням.

1. Рівняння (11.7) містить х і у тільки в парних степенях, якщо точка (х;у) належить еліпсу, то йому також належать точки (х;-у), (-х;у), (-х;-у). Звідси витікає, що еліпс симетричний відносно осі Ох і Оу, а також відносно точки O(0; 0), яку називають центром еліпса.

рис. 28.

2. Знайдемо точки перетину еліпса з осями координат. Поклавши у=0, знаходимо дві точки А₁(а; 0) і A₂(-а; 0), в яких вісь Ох перетинає еліпс (див. рис. 28). Поклавши в рівнянні (3.7) х = 0, знаходимо точки перетину еліпса з віссю Оу: B₁(0;b) і В₂(0;-b). Точки A₁, A₂, B₁, В₂ називаються вершинами еліпса. Відрізки A₁A₂ і B₁В₂, а також їх довжини 2а і 2b називаються великою і малою осями еліпса. Числа а і b називаються відповідно великою і малою пів осями еліпса.

3. З рівняння (3.7) виходить, що кожен доданок в лівій частині не перевершує одиниці, тобто мають місце нерівності і або і. Отже, всі точки еліпса лежать усередині прямокутника, утвореного прямими х = ± a, у = ± b.

4. У рівнянні (3.7) сума невід’ємних доданків і рівна одиниці. Отже, при зростанні одного доданку інше зменшуватиметься, тобто якщо |х| зростає, то | у| зменшується і навпаки.

Додаткові відомості про еліпс

Форма еліпса залежить від відношення 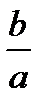. При b = а еліпс перетворюється на коло, рівняння еліпса (3.7) приймає вид х² +у² = а². Як характеристика форми еліпса частіше користуються відношенням .

Відношення половина відстані між фокусами і великої півосі еліпса називається ексцентриситетом еліпса і позначається буквою («эпсилон»):

(3.8)

причому 0<<1, оскільки 0<с<а. З урахуванням рівності (3.6) формулу (3.8) можна переписати у вигляді

,

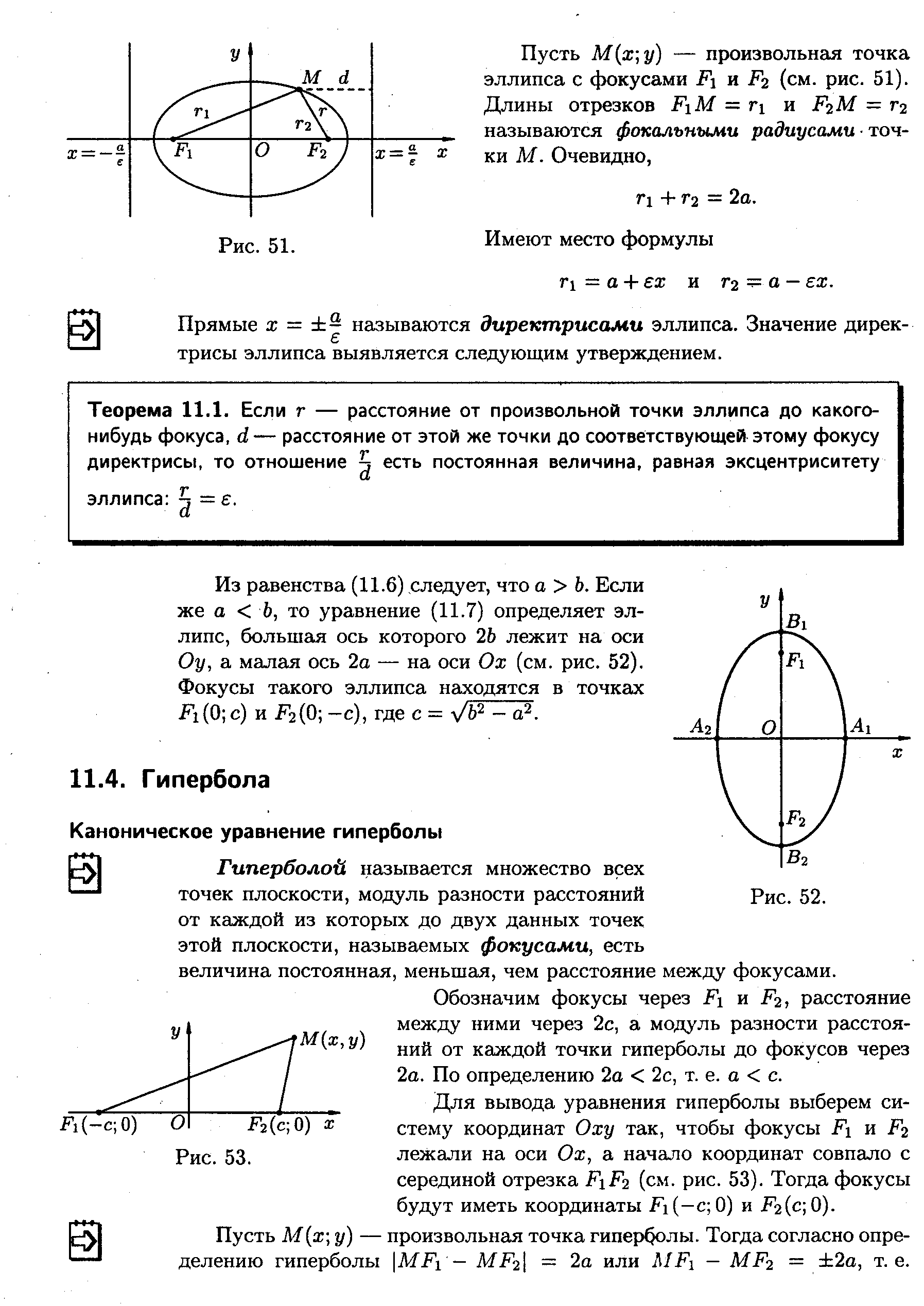
рис. 29.

тобто

і

Звідси видно, що чим менше ексцентриситет еліпса, тим еліпс буде менш сплюснутим; якщо покласти = 0, то еліпс перетворюється на коло.

Нехай М(х;у) — довільна точка еліпса з фокусами F ₁і F ₂(див. рис. 29).

Довжини відрізків F ₁ М = r ₁, і F ₂ М = r ₂ називаються фокальними радіусами точки М. Очевидно,

r ₁ + r ₂ =2a.

мають місце формули

і .

Прямі називаються директрисами еліпса. Значення директриси еліпса виявляється наступним твердженням

Теорема 3.1. Якщо r — відстань від довільної точки еліпса до якого-небудь фокуса, d — відстань від цієї ж точки до відповідної цьому фокусу директриси, то відношення 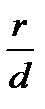є постійною величиною, що дорівнює ексцентриситету еліпса: .

рис. 30.

З рівності (3.6) випливає, що a > b. Якщо ж a < b, то рівняння (3.7) визначає еліпс, велика вісь якого 2 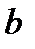лежить на осі Оу, а мала вісь 2а — на осі Ох (див. рис. 30). Фокуси такого еліпса знаходяться в точках F₁(0;с) і F₂(0;-с), де .

3.3.4. Гіпербола

Канонічне рівняння гіперболи

Гіперболою називається множина всіх точок площини. Модуль різниці відстаней від кожної з яких до двох даних точок цієї площини, що називаються фокусами, є величина постійна, менша за відстань між фокусами.

Позначимо фокуси через F ₁і F ₂, відстань між ними через 2с, а модуль різниці відстаней від кожної точки гіперболи до фокусів через 2а. За означенням 2а<2с, тобто а<с.

рис. 31.

Для виводу рівняння гіперболи виберемо систему координат Оху так, щоб фокуси F ₁і F ₂ лежали на осі Ох, а початок координат співпав з серединою відрізка F ₁ F ₂ (див. рис. 31). Тоді фокуси будуть мати координати F ₁ (- с;0) і F ₂(с;0).

Нехай М(х; у) — довільна точка гіперболи. Тоді, згідно означенню гіперболи,

|МF₁–МF₂|=2а або МF₁–МF₂=±2a, тобто . Після спрощень, як це було зроблено при виводі рівняння еліпса, отримаємо канонічне рівняння гіперболи.

, (3.9)

де

. (3.10)

Гіпербола є лінією другого порядку.

Дослідження форми гіперболи за її рівнянням

Установимо форму гіперболи, використовуючи її канонічне рівняння.

1. Рівняння (3.9) містить х і у тільки в парних степенях. Відповідно, гіпербола симетрична відносно осей Ох і Оу, а також відносно точки O(0; 0), яку називають центром гіперболи.

2. Знайдемо точки перетину гіперболи з осями координат. Поклавши у = 0 в рівнянні (11.9), знайдемо дві точки перетину гіперболи з віссю Ох: A ₁ (a;0) і A ₂ (-а;0). Поклавши в (3.9), отримаємо у² = -b², чого не може бути. Відповідно, гіпербола вісь Оу не перетинає.

Точки А ₁ (а;0) і A ₂ (-а;0) називаються вершинами гіперболи, а відрізок А ₁ А ₂ =2а — дійсною віссю, відрізок ОА ₁ =ОА ₂ =а — дійсною піввіссю гіперболи.

Відрізок В ₁ В ₂ (В ₁ В ₂ = 2b), що з’єднує точки В ₁ (0; b) і В ₂ (0;- b) називається уявною віссю, число b — уявною піввіссю. Прямокутник зі сторонами 2а і 2b називається основним прямокутником гіперболи.

3. З рівняння (3.9) випливає, що зменшуване не менше за одиницю, тобто що або . Це означає, що точки гіперболи розташовані справа від прямої х=а (права гілка гіперболи) і зліва від прямої х = - а ( ліва гілкагіперболи).

4. З рівняння (3.9) гіперболи видно, що коли |х| збільшується, то і |у| збільшується. Це випливає з того, що різниця 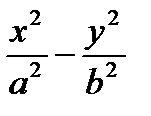зберігає постійне значення, рівне одиниці.

рис. 32.

Із сказаного випливає, що гіпербола має форму, зображену на рис. 32 (крива, яка складається з двох необмежених гілок).

рис. 33.

рис. 34.

Асимптоти гіперболи

Пряма L називається асимптотою необмеженої кривої К, якщо відстань d від точки М кривої К до цієї прямої прямує до нуля при необмеженому віддаленні точки М вздовж кривої К віл початку координат. На рис. 33 наведена ілюстрація поняття асимптоти: пряма L являється асимптотою для кривої K.

Покажемо, що гіпербола має дві асимптоти:

і . (3.11)

Оскільки прямі (3.11) і гіпербола (3.9) симетричні відносно координатних осей, то достатньо розглянути тільки ті точки указаних ліній, які розташовуються в першій чверті.

Візьмемо на прямій точку N, що має ту ж абсцису. Що і точка М(x;y) на гіперболі (див. рис. 34), і знайдемо різницю MN між ординатами прямої і гілки гіперболи:

рис. 34.

Як видно, по мірі росту х знаменник дробу збільшується; чисельник – є постійна величина. Тобто, довжина відрізка МN прямує до нуля. Оскільки MN більше за відстань d від точки М до прямої, то d тим більше прямує до нуля. Так, прямі

являються асимптотами гіперболи (11.9).

При побудові гіперболи (11.9) зручно спочатку побудувати основний прямокутник гіперболи (див. рис. 35), провести прямі, що проходять через протилежні вершини цього прямокутника

рис. 35.

, — асимптоти гіперболи і відмітити вершини А ₁ і A ₂ гіперболи.

Рівняння рівносторонньої гіперболи, асимптотами якої є координатні осі.

Гіпербола (3.9) називається рівносторонньою, якщо її піввісь рівні (а = b). ЇЇ канонічне рівняння

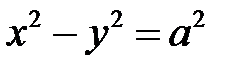. (3.12)

Асимптоти рівносторонньої гіперболи мають рівняння у=х і у=–х і, відповідно, являються бісектрисами координатних кутів.

Розглянемо рівняння цієї гіперболи в новій системі координат (див. мал. 36), отриманої з старої поворотом осей координат на кут 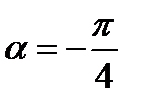. Використаємо формули повороту осей координат:

Підставляємо значення х і у в рівняння (3.12):

,

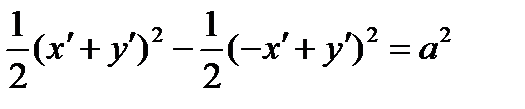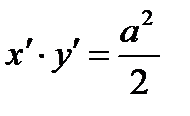, , або ,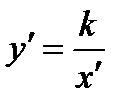

де .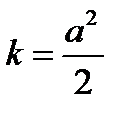

Рівняння рівносторонньої гіперболи, для якої вісі Ох і Оу являються асимптотами, буде мати вигляд .

Додаткові відомості про гіперболу

Ексцентриситетом гіперболи (3.9) називається відношення відстані між фокусами і величиною дійсної осі гіперболи, позначається :

.

Оскільки для гіперболи , то ексцентриситет гіперболи більший за одиницю: . Ексцентриситет характеризує форму гіперболи. Дійсно, з рівності (11.10) слідує, що 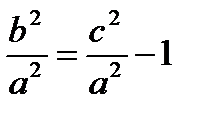, тобто і .

Звідси видно. Що чим менший ексцентриситет гіперболи, тим меншим є відношення 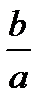її півосей, а, значить, тим більш витягнутим є її основний прямокутник.

Ексцентриситет рівносторонньої гіперболи дорівнює . Дійсно,

Фокальні радіуси і 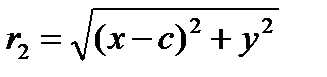для точок правої гілки гіперболи мають вигляд 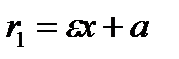і 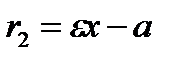, а для лівої і .

Прямі називаються директрисами гіперболи. Оскільки для гіперболи , то . Це означає, що права директриса розташована між центром і правою вершиною гіперболи, ліва – між центром і лівою вершиною.

Директриси гіперболи мають ту ж властивість , що і директриси еліпса.

Крива, що визначається рівнянням , також є гіперболою, дійсна вісь 2 b якої розташована на осі Оу, а уявна вісь 2a — на осі Ох. На рис. 36 вона зображена пунктиром.

рис. 36.

рис. 36.

Очевидно, що гіперболи і мають спільні асимптоти. Такі гіперболи називаються спряженими.

Парабола

Канонічне рівняння параболи.

Параболою називається множина всіх точок площини, кожна з яких однаково віддалена від даної точки, що називається фокусом, і даної прямої, яка називається директрисою. Відстань від фокуса F до директриси називається параметром параболи і позначається через р (р > 0).

Для виводу рівняння параболи оберемо систему координат Оху так, щоб вісь Ох проходила через фокус F перпендикулярно директрисі в напрямку від директриси до F, а початок координат О розташуємо посередині між фокусом і директрисою (див. рис. 37). В вибраній системі фокус F має координати (; 0), а рівняння директриси має вигляд 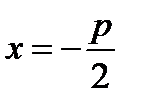або .

рис. 37.

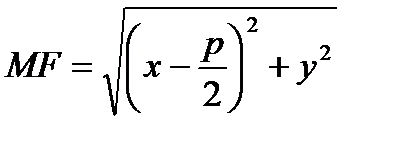Нехай М(x; у) — довільна точка параболи. З’єднаємо точку М з F. Проведемо відрізок МN перпендикулярно директрисі. Згідно означення параболи МF = МN. А з формулою відстані між двома точками знаходимо:

, а .

Тобто,

.

Піднісши обидві частини рівняння до квадрату, отримаємо

,

тобто

(3.13)

Рівняння (3.13) називається канонічним рівнянням параболи. Парабола – лінія другого порядку.

Дослідження форм параболи за її рівнянням.

1. В рівнянні (3.13) змінна у входить в парному степені, значить, парабола симетрична відносно вісі Ох; вісь Ох є віссю симетрії параболи.

2. Оскільки р > 0, то з (3.13) слідує, що 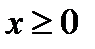. Тобто, парабола розташована справа від осі Оу.

3. При х = 0 маємо у = 0. Відповідно, парабола проходить через початок координат.

рис. 38.

4. При необмеженому зростанні х модуль у також необмежено зростає. Парабола у²=2рх має вигляд(форму), зображений на рис. 38. Точка О(0;0) називається вершиною параболи, відрізок FМ = r називається фокальнимрадіусом точки М.

Рівняння у² = -2рх, х² = 2ру, х² = -2ру (р > 0) також визначають параболи. Вони зображені на рис. 39.

рис. 39.

Неважко показати, що графік квадратного тричлена у = Ах² + Вх + С, где , В і С довільні дійсні числа, представляє собою параболу в сенсі наведеного вище її означення.

3.3.6. Загальне рівняння лінії другого порядку

Рівняння кривих другого порядку з осями симетрії, паралельними координатним осям

рис. 40.

Знайдемо спочатку рівняння еліпса з центром в точці O ₁ (x₀; y₀), осі симетрії якого паралельна координатним осям Ох і Оу і півосі відповідно рівні a і b. Помістимо в центрі еліпса O ₁ початок нової системи координат O ₁ х'у', вісі якої O ₁ х' і O ₁ у' паралельні відповідним осям Ох і Оу і однаково з ними напрямлені (див. рис. 40). В цій системі координат рівняння еліпса має вигляд

.

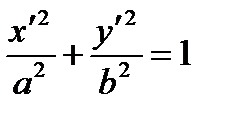Оскільки х' = х – х ₀, у' = х - у ₀, то в старій системі координат рівняння еліпса запишеться у вигляді

.

Аналогічно міркуючи, отримаємо рівняння гіперболи з центром в точці O ₁ (х ₀; у ₀ ) і півосями а і b (див. рис. 41):

.

рис. 41.

І нарешті параболи, зображені на рис. 42, мають відповідні рівняння.

⇐ Предыдущая 12

Не нашли, что искали? Воспользуйтесь поиском: