
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Гідротехнічні поняття
Нормально підпертий рівень або горизонт (НПР, НПГ) – рівень вільної поверхні води у водосховищі, що спостерігається протягом більшої частини року.
Форсований підпертий рівень або горизонт (ФПР, ФПГ) – рівень вільної поверхні води у водосховищі, що спостерігається під час повені, повіддя. За відсутності даних приймається ФПР = НПР + 2 м.
Мертвий об’єм водосховища – об’єм, що залишається при повному спорожненні водосховища. За відсутністю даних його приймають рівним 5% корисного об’єму водосховища.
Повний об’єм водосховища є сумою корисного й мертвого об’ємів. Повний об’єм відповідає відмітці НПР.
Потрібний об’єм водосховища дорівнює об’єму водоспоживання з урахуванням витрат води на фільтрацію та випаровування з поверхні водосховища. У випадку відсутності конкретних даних потрібний об’єм приймається на 10 … 20 % більший, ніж об’єм водоспоживання.
2 Основи математичної статистики, які використовується у курсовій роботі
Якщо гідрологічна характеристика (наприклад, витрата, рівень води у річці) безперервна, то вірогідність появи фіксованого значення дорівнює нулю. Вірогідність визначається як відношення кількості появ фіксованого значення до загальної кількості. Якщо величина безперервна, то загальна кількість, хоча б на обмеженому інтервалі, є величиною нескінченно великою. Скорочений запис – 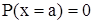 . Щоб уникнути цього, в гідрології використовується величину
. Щоб уникнути цього, в гідрології використовується величину  , яка називається функція розподілу. Величина
, яка називається функція розподілу. Величина 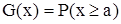 називається функцією забезпеченості. Зв’язок між функціями розподілу та забезпеченості такий:
називається функцією забезпеченості. Зв’язок між функціями розподілу та забезпеченості такий:
 .
.
Одна з властивостей функції забезпеченості –спадаюча: значення гідрологічної характеристики при зростанні забезпеченості зменшується. В подальшому витрату забезпеченості "Р" будемо позначати QP. Якщо витрата 95% забезпеченості дорівнює 17 м3/с (Q95=17 м3/с), то це означає, що протягом спостереження 100 років, 95 років витрата буде не менша 17 м3/с, а впродовж 5-ти років – менша ніж 17 м3/с.
Відомо, що, якими б довгими ряди спостережень не були, на межах інтервалу даних недостатньо, і визначення гідрологічних характеристик як малої, так і великої забезпеченості є недостовірним. Для усунення цього недоліку підбирається теоретична крива розподілу так, щоб більша частина даних співпадала з нею. Як наслідок, дані на межах інтервалу, визначені за теоретичною, кривою будуть більш обґрунтовані з точки зору вірогідності.
Підбір теоретичної кривої може бути виконано трьома способами:
– методом моментів;
– методом максимальної правдоподібності;
– методом квантилів.
У даній роботі використовується метод квантилів. За експериментальною кривою забезпеченості визначаються вірогідності трьох значень гідрологічної характеристики (які називаються квантилі) 5, 50 та 95% забезпеченості. (В подальшому під гідрологічною характеристикою буде розумітися середньорічна витрата і позначатиметься Q5, Q50 та Q95.)
Визначається коефіцієнт скошеності за залежністю
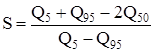 . (2.1)
. (2.1)
За додатком В (табл. В.1) визначають нормовані ординати біноміальної кривої розподілу Ф5, Ф50 та Ф95, які відповідають підрахованому значенню S (коефіцієнт асиметрії СS однозначно пов’язаний з коефіцієнтом скошеності S) при значенні СV=1.
Загальний вираз для витрати забезпеченості "Р" такий:
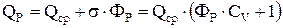 . (2.2)
. (2.2)
Отже маємо три рівняння:
 ,
,
 ,
,
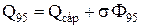 .
.
Звідси
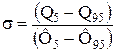 , (2.3)
, (2.3)
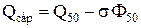 ,
,
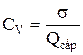 .
.
В гідрології витрати різної забезпеченості мають назви, наведені в таблиці 2.1.
У таблиці 2.1 останні два рядки заповнюються конкретними цифрами під час виконання курсової роботи.
Попередні розрахунки витрати стосувалися середньорічної витрати. Але визначення відміток кріплення споруд насосної станції першого підйому, витрату скидів систем оборотного водоспоживання (так звана продувка системи) виконується за витратами малої забезпеченості для весняної повені. У разі відсутності досліджень витрат у період повені по регіонах України можливо обмежитись короткими рядами досліджень. А статистичну обробку виконують у припущенні, що кожен член ряду уособлює характеристику певної кількості спостережень у деякому інтервалі значень. У залежності від цієї характеристики здобуто чотири формули для визначення забезпеченості при коротких рядах досліджень.
Таблиця 2.1 – Витрати забезпеченості
| Назва водності | Багатоводний | Середньо-багатоводний | Помірно-багатоводний | Середньо-водний | Помірно-маловодний | Середньо-маловодний | Маловодний | Дуже маловодний |
| Забезпеченість Р, % | ||||||||
| Коефіцієнт Ф | ||||||||
| Витрата QP, м3/с |
Хазен припустив, що фіксоване значення відноситься до середини цього інтервалу:
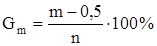 . (2.4)
. (2.4)
де m – порядковий номер витрати в ранжированому ряді (ранжирований ряд – витрати розташовують від найбільшого значення – перший номер, до найменшого – останній номер),
n – загальна кількість членів ряду.
Крицький та Менкель вважали, що найбільш точно забезпеченість відповідає середньому значенню членів ряду:
 . (2.5)
. (2.5)
Чегодаєв припустив, що емпіричні дані займають медіанне розташування серед усіх можливих значень:
 . (2.6)
. (2.6)
Блохінов на підставі усереднення багатьох експериментальних даних дійшов висновку, що їм відповідає залежність забезпеченості у вигляді
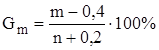 . (2.7)
. (2.7)
У гідрологічній літературі пострадянських країн використовуються залежності Крицького – Менкеля і Чегодаєва.
Не нашли, что искали? Воспользуйтесь поиском: