Определение и использование пользовательских функций

Важным инструментом в математических вычислениях являются пользовательские функции. Функции особенно целесообразно использовать, когда приходиться производит многократные вычисления по одним и тем же формулам, но с разными исходными данными.

Чтобы воспользоваться собственной функцией, нужно:

1. Описать функцию.

2. Вызвать описанную функцию для выполнения.

Для определения функции используются идентификаторы: имя функции и имена формальных параметров функции.

Формальный параметр – это идентификатор, конкретное значение которого определяется путём замены его на соответствующее ему значение фактического параметра при обращении к функции. Функции однозначно ставят в соответствие значениям аргументов (формальным параметрам) значения фактических параметров функции.

Формат определения функции:

Имя_функции (список формальных параметров):=выражение

Вызов пользовательской функции производится подобно тому, как в случае вызова любой стандартной функции.

Можно поместить результат в отдельную переменную:

Имя_переменной_результата:=Имя_функции (список формальных параметров)

Или напечатать:

Имя_функции(список формальных параметров)=

Пример 1. Требуется определить функцию Dist, которая будет возвращать расстояние заданной точки от начала координат. Использовать эту функцию для вычисления расстояния от точки А (1.96; –3.8) и В (6; 42.5) до начала координат.

Решение. Из курса линейной алгебры известно, что расстояние от начала координат до некоторой точки A (x, y) определяется по формуле 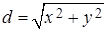. Здесь (x, y) – координаты заданной точки. Эта формула и будет составлять основу функции Dist. При описании функции следует предусмотреть два формальных параметра – координаты точки. На это место этих параметров должны будут вписаны фактические координаты заданных точек.

В соответствии с формулой определения расстояния от точки на плоскости до начала координат функция Dist может быть записана в виде: .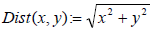

А обращение к функции для вычислений расстояний от заданных точек может быть представлено как:

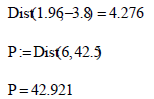
Во втором случае результат помещается во вспомогательную переменную.

1.1.7.3. Определение переменных, принимающих значения
из заданного промежутка

В системе MathCAD предоставлена возможность определения переменных, принимающих значения из заданного промежутка, причём соседние значения удалены на равные расстояния друг от друга. При этом задаётся только начальное значение, следующее значение и конечное значение.

В качестве переменных, принимающих значение из промежутка, можно использовать только идентификаторы без индексов.

Формат определения переменной:

Имя_переменной:= начальное_значение, начальное _значение + шаг.. конечное_значение.

Если конечное значение при данном значении шага не достигается точно, последним значением переменной будет наибольшее значение из заданного промежутка, не превышающее конечное значение.

Кроме того MathCAD предоставляет возможность не задавать следующее значение, если шаг по величине совпадает со значением 1 или –1.

В этом случае формат определения переменной можно представить в виде:

Имя_переменной:= начальное_значение.. конечное_значение

Пример 2. Требуется получить таблицу значений функции 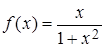на интервале [ a, b ] с шагом h.

Решение. Решение задачи можно свести к выполнению следующих шагов:

1. Определить функцию f (x).

2. Задать a, b, h.

3. Задать переменную (например, t), принимающую значение из промежутка на интервале [ a, b ] с шагом h.

4. Получить таблицу значений функции для переменной t.

5. На рис. 6. представлен фрагмент документа с решением задачи.

Рис. 6. Получение таблицы значений функции
на заданном интервале с постоянным шагом

Не нашли, что искали? Воспользуйтесь поиском: