
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
ПРИМЕР ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ
Задание:
Для заданной электрической цепи постоянного тока требуется найти:
1. Токи во всех ветвях и напряжение между точками А и В.
2. Составить уравнение баланса мощностей.
3. Построить потенциальную диаграмму для внешнего контура.
Дано:
 Ом,
Ом, 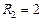 Ом,
Ом, 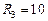 Ом,
Ом, 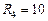 Ом,
Ом,  Ом,
Ом, 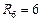 Ом,
Ом, 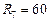 Ом,
Ом, 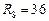 Ом,
Ом, 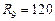 Ом,
Ом, 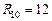 Ом
Ом
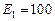 В,
В, 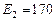 В,
В, 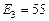 В,
В, 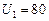 В,
В, 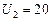 В
В
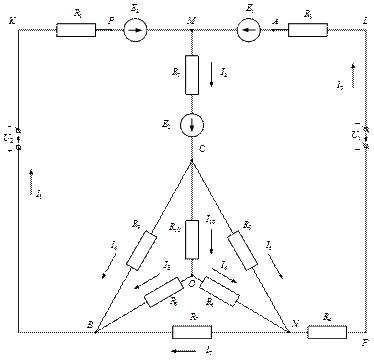
Рис. 8. Исходная схема сложной электрической цепи
Решение:
1. Выберем условно – положительные направления искомых токов во всех ветвях схемы  . Обозначим на схеме характерные точки цепи – узлы цепи и точки между соседними элементами цепи, отличающиеся между собой потенциалами, точку с нулевым потенциалом.
. Обозначим на схеме характерные точки цепи – узлы цепи и точки между соседними элементами цепи, отличающиеся между собой потенциалами, точку с нулевым потенциалом.
2. Метод преобразования электрической цепи. Преобразованию подвергаются ветви с резистивными (пассивными) элементами, т.е. такие ветви, которые не содержат источников ЭДС и напряжений. Установить:
· есть ли параллельные соединения резисторов, отсутствуют;
· есть ли последовательные соединения, 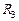 и
и 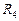 соединены последовательно:
соединены последовательно:
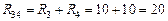 Ом;
Ом;
· есть ли в схеме соединения резисторов по схеме «звезда» и «треугольник», если есть решить вопрос о целесообразности преобразования «звезды» в «треугольник» или наоборот.
Преобразуем «звезду» 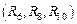 в треугольник
в треугольник  :
:
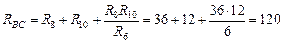 Ом;
Ом;
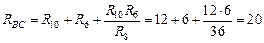 Ом;
Ом;
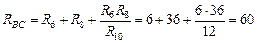 Ом..
Ом..
После преобразования получаются параллельные соединения резисторов, которые также преобразуются:
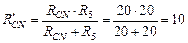 Ом;
Ом;
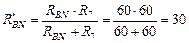 Ом;
Ом;
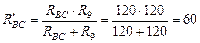 Ом.
Ом.
На рис.9 показаны этапы преобразования исходной схемы

Рис. 9. Этапы преобразования исходной схемы
В получившейся схеме, преобразуем «треугольник» резисторов 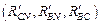 в «звезду»
в «звезду» 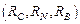 .
.
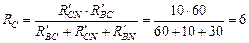 Ом;
Ом;
 Ом;
Ом;
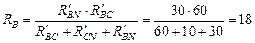 Ом.
Ом.
Получим схему «звезда» с новым узлом 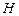 . Заменив исходную схему с учётом выполненных преобразований, получим упрощённую схему электрической цепи, содержащую только два контура (рис.10).
. Заменив исходную схему с учётом выполненных преобразований, получим упрощённую схему электрической цепи, содержащую только два контура (рис.10).
Не имеет смысла объединять последовательно соединенные сопротивления 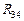 и
и 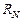 ,
, 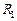 и
и  , так как исчезнут точки
, так как исчезнут точки 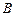 и
и 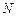 , из-за чего не возможно будет определить потенциалы в этих точках.
, из-за чего не возможно будет определить потенциалы в этих точках.
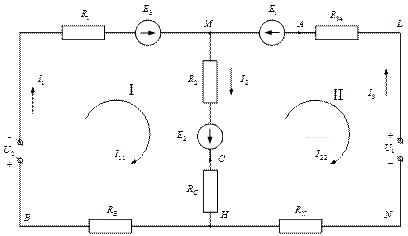
Рис.10. Упрощённая схема электрической цепи
3. Найдём токи полученной схемы (рис.10) используя метод непосредственного применения законов Кирхгофа.
· Определить количество ветвей 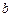 и количество узлов
и количество узлов 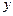 :
:
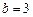 ,
, 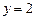 .
.
· Выделить независимые контуры и произвольно принять их положительные направления обходов.
· Составить 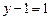 уравнение по 1 – му закону Кирхгофа и
уравнение по 1 – му закону Кирхгофа и 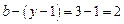 уравнения по 2 – му закону Кирхгофа. Для узла
уравнения по 2 – му закону Кирхгофа. Для узла 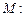
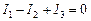 .
.
Для контура I:
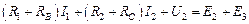 .
.
Для контура II:
 .
.
· Подставить исходные данные в полученную систему уравнений и решить её:
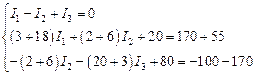

Данную систему уравнений можно решить, используя, например, математический пакет MATLAB. Для этого в командном окне необходимо ввести:
>> A=[1 -1 1
21 8 0
0 8 23]
A =
1 -1 1
21 8 0
0 8 23
>> B= [0
350]
B =
>> X = A\B
X =
4.2575
14.4491
10.1916
>>
Таким образом, получим токи:
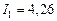 А,
А, 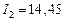 А,
А,  А
А
Токи получились положительными, т.е. произвольно принятые направления токов совпали с их действительными направлениями.
4. Найдём токи полученной схемы (рис.10) используя метод контурных токов.
· Составить 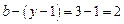 уравнения по 2 – му закону Кирхгофа для контуров I и II.
уравнения по 2 – му закону Кирхгофа для контуров I и II.
Для контура I:
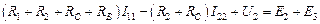 .
.
Для контура II:
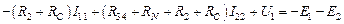 .
.
· Подставить исходные данные в полученную систему уравнений и решить её:
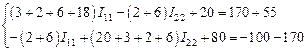
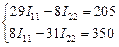
Чтобы решить данную систему, в командном окне MATLAB введем следующие команды:
>> A = [29 -8
8 -31]
A =
29 -8
8 -31
>> B = [205
350]
B =
>> X = A\B
X =
4.2575
-10.1916
>>
Таким образом, получим контурные токи:
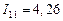 А,
А, 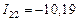 А.
А.
Тогда искомые токи будут
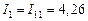 А,
А,
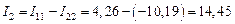 А,
А,
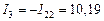 А
А
5. Найдём токи полученной схемы (рис.10) методом двух узлов.
· Перечертить схему (рис.10) заменив все источники напряжения источниками ЭДС. С направлениями, противоположными направлениям напряжения.
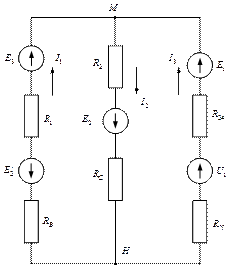
Рис.11. Упрощённая схема с заменёнными источниками напряжения
· Вычислить проводимости ветвей схемы
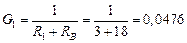 См;
См;
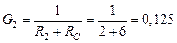 См;
См;
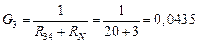 См;
См;
· Вычислить узловое напряжение

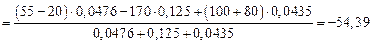 В.
В.
· Вычислить токи в ветвях:
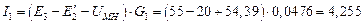 А,
А,
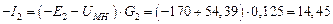 А,
А,
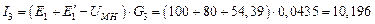 А.
А.
6. Переход от упрощённой схемы к исходной.:
· Найти по 2 – му закону Кирхгофа напряжения между теми узлами и характерными точками упрощённой схемы, которые образуют ветви в исходной электрической цепи. Для нахождения в исходной схеме (рис.8) токов 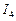 ,
, 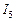 ,
, 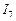 необходимо знать напряжения между узлами
необходимо знать напряжения между узлами 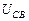 ,
,  ,
, 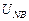 . Эти напряжения найдём из упрощённой схемы.
. Эти напряжения найдём из упрощённой схемы.
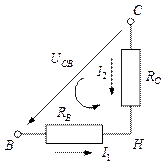
Для контура 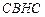 :
:
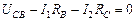 ,
,
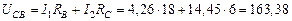 В
В
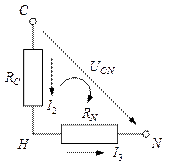
Для контура 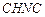 :
:
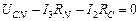 ,
,
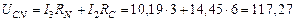 В
В
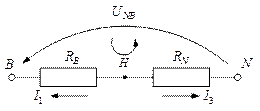
Для контура 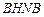 :
:
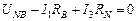 ,
,
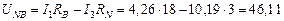 В
В
· Определим токи в ветвях исходной схемы (рис.8) по закону Ома:
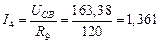 А,
А, 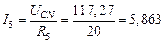 А,
А, 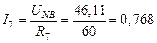 А.
А.
· Определить узлы, в которых известны все токи, кроме одного. Это узлы 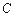 ,
, 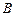 ,
, 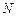 . По 1 – му закону Кирхгофа определить в этих узлах неизвестные токи
. По 1 – му закону Кирхгофа определить в этих узлах неизвестные токи
Для узла 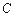 :
:
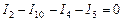 ,
,
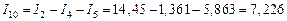 А.
А.
Для узла 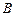 :
:
 ,
,
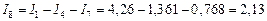 А.
А.
Для узла 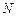 :
:
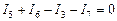 ,
,
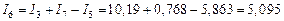 А.
А.
Если ещё остались неизвестные токи, определить их по 2 – му закону Кирхгофа, рассмотрев те контуры, в которые эти токи входят.
7. Нахождение напряжения между двумя характерными точками.
· Ввести искомое напряжение между заданными узлами или характерными точками цепи, обозначив это напряжение соответствующей стрелкой на схеме.
· Выделить один любой контур из образованных искомым напряжением.
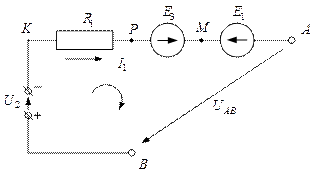
Для контура 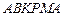 :
:
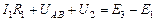 ,
,
 В
В
8. Баланс мощностей.
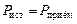 ,
,
 .
.
Вырабатываемая мощность источником, режим работы которого характеризуется совпадением направлений его ЭДС и тока через него
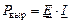 .
.
Отдаваемая мощность источником, режим работы которого характеризуется несовпадением направлений напряжения на его клеммах и тока через него
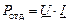 .
.
Преобразуемая мощность – мощность, которая потребляется при преобразовании электрической энергии в другие виды энергии источником, имеющим ЭДС и ток разных направлений (например, преобразуемая мощность при зарядке аккумуляторных батарей)
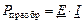 .
.
Потребляемая мощность приёмником, режим работы которого характеризуется совпадением направлений приложенного к нему напряжения и тока через него
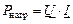 .
.
Потребляемая мощность, выделяемая в виде тепла на элементе цепи с сопротивлением 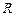 и на внутреннем сопротивлении источника
и на внутреннем сопротивлении источника
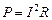 .
.
В соответствии с выше изложенным, составим баланс мощности:
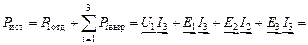
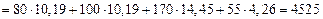 Вт
Вт
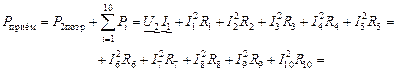
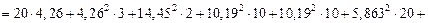
 Вт
Вт
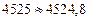 – баланс мощностей сходится.
– баланс мощностей сходится.
9. Потенциальная диаграмма графически изображает 2 – й закон Кирхгофа. Сумма потенциалов в замкнутом контуре электрической цепи равна нулю
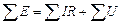 ,
,
или
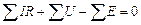 .
.
Следовательно, одну из точек цепи, например, точку 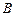 , можно заземлить, а потенциал её приравнять к нулю.
, можно заземлить, а потенциал её приравнять к нулю.
Выделим из рассчитанной электрической цепи внешний контур:
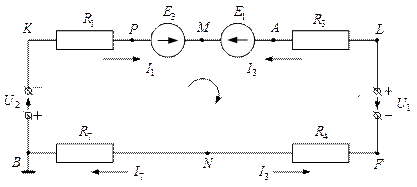
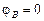 В,
В,
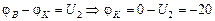 В,
В,
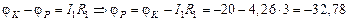 В,
В,
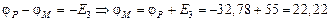 В,
В,
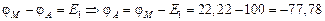 В,
В,
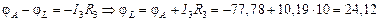 В,
В,
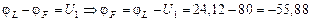 В,
В,
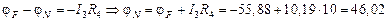 В,
В,
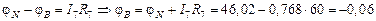 В.
В.
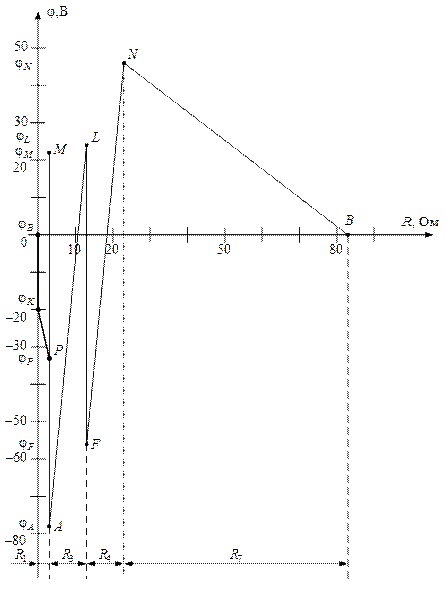
Рис. 12. Потенциальная диаграмма для внешнего контура
исходной электрической цепи
ВАРИАНТЫ ЗАДАНИЙ
| Вар. | Рис.№ | 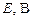
| 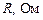
| Вар. | Рис.№ | 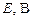
| 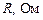
|

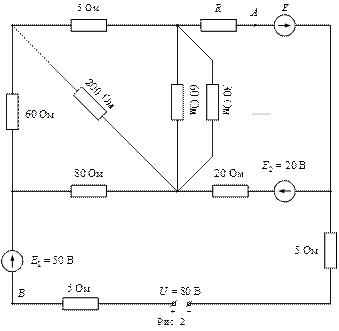
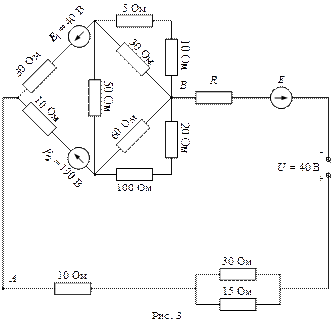
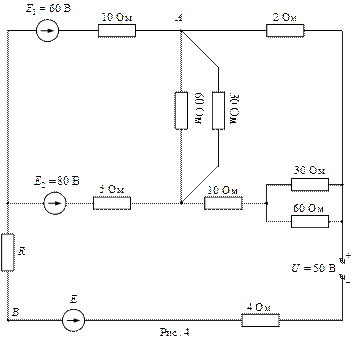
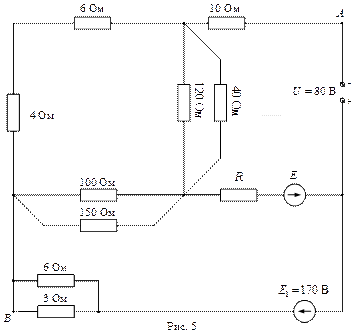
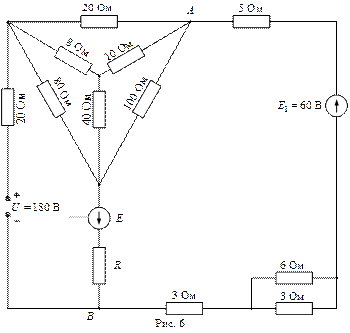

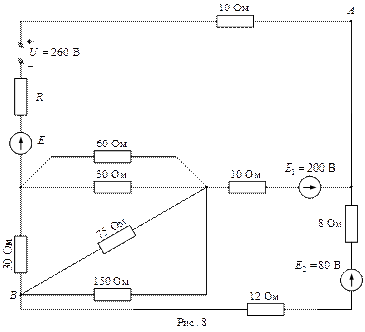
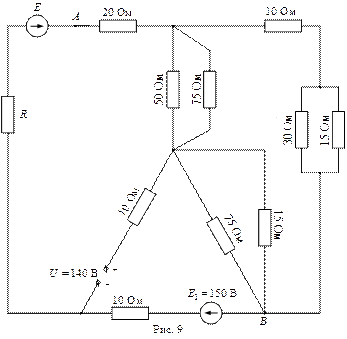
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Иванов И.И., Соловьев Г.И., Фролов В.Я. Электротехника и основы электроники. Учебник. 7-изд., перераб. и доп. СПб.: Издательство «Лань», 2012. – 736 с.: ил.
2. А.С. Касаткин, М.В. Немцов. Электротехника: учеб. для вузов М: Издательский центр «Академия», 2008 - 544 с.
3. Иванов И. И., Соловьев Г.И., Фролов В.Я. Электротехника и основы электроники. Учебник. 7-изд., перераб. и доп. СПб.: Издательство «Лань», 2012. – 736 с.: ил. http://e.lanbook.com/books/element.php?pl1_cid=25&pl1_id=3190
4. Белов Н.В., Волков Ю.С. Электротехника и основы электроники. Учебное пособие. 1-изд., Издательство «Лань», 2012. – 432 с.: http://e.lanbook.com/books/element.php?pl1_cid=25&pl1_id=355.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ …3
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ …4
Законы Ома и Кирхгофа …4
Метод преобразования …5
Не нашли, что искали? Воспользуйтесь поиском: