
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Метод парных сравнений
Метод парных сравнений позволяет не только ранжировать (упорядочить) объекты по некоторому критерию, но также рассчитать числовые значения их относительной значимости. Метод заключается в заполнении матрицы парных сравнений A, которая для объектов M 1, M 2, … Mn имеет вид:
| M 1 | M 2 | … | Mn | |
| M 1 | a 12 | … | a 1 n | |
| M 2 | 
| … | a 2 n | |
| … | … | … | … | … |
| Mn | 
| 
| … |
Значения элементов aij матрицы определяются по шкале относительной важности (таблица 1) в зависимости от соотношения элементов Mi и Mj: если элемент Mi превосходит Mj, в i -ю строку и j -й столбец матрицы заносится целое число, а в j -ю строку и i -й столбец – обратное к нему число.
Матрица парных сравнений – обратно симметричная. Диагональ матрицы состоит из единиц.
Таблица 1 - Шкала относительной важности элементов
| Относительная важность | Уровень важности | Комментарии |
| Равная важность | Элементы вносят одинаковый вклад | |
| Слабое превосходство | Опыт и суждения дают легкое предпочтение первого элемента над вторым | |
| Существенное превосходство | Опыт и суждения дают сильное предпочтение первого элемента над вторым | |
| Значительное превосходство | Превосходство первого элемента над вторым очень сильно и практически явно | |
| Абсолютное превосходство | Свидетельства о превосходстве первого элемента над вторым в высшей степени убедительны | |
| 2, 4, 6, 8 | Промежуточные значения | Используются при компромиссных решениях |
Например, при сравнении площади трех объектов, представленных на рисунке, матрица может иметь следующий вид. Здесь эксперт оценил превосходство объекта M 3 над двумя другими объектами равными значениями (9), посчитав, что различием можно пренебречь:

| M 1 | M 2 | M 3 |
| M 1 | 1/9 | ||
| M 2 | 1/3 | 1/9 | |
| M 3 |
Коэффициенты важности объектов рассчитываются как средние геометрические по каждой строке матрицы (bi), а затем нормализуются (wi), чтобы в сумме давать единицу:
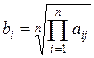 ;
;  .
.
В рассмотренном примере:
 ;
;  ;
;  ;
;
 ;
;  ;
;  .
.
Проверка согласованности. Основная сложность при построении матрицы парных сравнений – обеспечение транзитивности суждений: если M 1 > M 2 и M 2 > M 3, должно выполняться M 1 > M 3. Иначе суждения не транзитивны, и матрица не согласована.
Индекс согласованности матрицы определяется как
ИС = (lmax – n)/(n – 1),
где lmax – максимальное собственное значение матрицы[†], n – количество сравниваемых объектов. Максимальное собственное значение матрицы можно оценить по формуле:
 , где
, где  , т.е.
, т.е.  .
.
В рассмотренном примере
 ,
,
 ;
;
индекс согласованности  .
.
Полученное значение индекса согласованности сопоставляется с табличным значением K – средним значением согласованности, рассчитанным для множества случайных матриц (таблица 2). Для согласованной матрицы отношение ОС = ИС / К не должно превышать значение 0,1. В противном случае считается, что матрица не согласована.
Таблица 2 – Средние значения согласованности случайных матриц
| Размер матрицы | ||||||||||
| K | 0,58 | 0,9 | 1,12 | 1,24 | 1,32 | 1,41 | 1,45 | 1,49 | 1,51 | 1,48 |
Для рассмотренного примера отношение значений согласованности
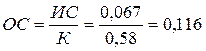 , что незначительно больше 0,1.
, что незначительно больше 0,1.
Если уточнить исходную матрицу сравнений и учесть разницу в соотношениях между объектами M 3- M 1 и M 3- M 2 (таблица 3), значение индекса согласованности улучшится: ИС = 0,055, ОС = 0,094 < 0,1.
Таблица 3 – Уточненная матрица сравнений
| M 1 | M 2 | M 3 | |
| M 1 | 1/8 | ||
| M 2 | 1/3 | 1/9 | |
| M 3 |
[*] Покупательная способность показывает, сколько товаров потребитель может купить на определённую сумму при существующем уровне цен
[†]Собственное значение квадратной матрицы – это такое число l, для которого существует вектор x (собственный вектор), такой что выполняется Ax = l x. У матрицы размером n ´ n существует ровно n собственных значений.
Не нашли, что искали? Воспользуйтесь поиском: