Лабораторная работа №2. Задание к лабораторной работе №2

Задание к лабораторной работе №2

1. Создать файл с данными своего варианта состоящего из 2 переменных и 84 случаев.

2. Вычислить дескриптивные (описательные) статистики выборок, относящихся к каждой из линий.

3. Построить гистограммы выборочных распределений и сформулировать предположения о законах распределений каждой из случайных величин.

4. Построить вариационный и интервальный ряд.

5. Используя критерии согласия, проверить гипотезы о законах распределения случайных величин.

6. Составьте отчёт о проделанной работе по вашему индивидуальному варианту.

Лабораторная работа №2

1. Для массового производства некоторых изделий компания планирует приобрести автоматическую линию. Рассматриваются варианты приобретения одной из двух моделей. Кондиционность изделий, произведённых этими линиями, определяется соответствием их веса номиналу 1,2 г. Допуски, в пределах которых изделие считается кондиционным, задаются интервалом [1,1; 1,3]. Специальные испытания, проведённые на этих линиях, дали следующие результаты, представленные в таблице 1.

Таблица 1. Исходные данные.

Файл с этими данными создается по следующей схеме:

- осуществляется вход в программу STATISTICA через модуль Basic Statistics/Tables (см. рис. 1);

Рисунок 1. STATISTICA Module Switcher

- затем последовательно выполняются команды File (Файл) → New Data (Новые данные) → Drivers (Диск) → h → File Name (Имя файла) → Ivanov1.STA → OK;

- программа автоматически открывает пустую электронную таблицу с именем Ivanov1.STA;

- в таблице делается 2 столбца, посредством последовательного выполнения команд Vars (Переменные) → Delete (Удалить) → From Variables (От переменной) → Var 3 → To Variables (До переменной) → Var 10 → OK;

- в таблице делается 84 строки, посредством последовательного выполнения команд Cases (Случаи) → Add (Добавить) → Number of Cases to Add (Количество добавляемых случаев) → 74 → OK;

- дважды щелкните мышью по белому полю в таблице под словами Data: Ivanov1.STA 2v*84c и заполните появившееся окно Data File Header (Заголовок файла данных) в соответствии с рис. 2;

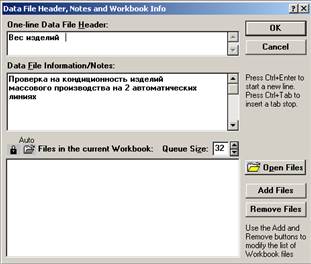
Рисунок 2. Data File Header, Notes and Workbook Info

- дважды щелкните мышью по имени переменной VAR1 и в поле Name (Имя) напишите Линия_№1. То же сделайте для переменной VAR2;

- для установки числа разрядов после десятичной точки равным 4 щелкните 1 раз мышью по имени переменной Линия_№1 и 1 раз по пиктограмме . То же сделайте для переменной Линия_№2;

- заполните полученную таблицу значениями результатов специальных испытаний, проведенных на двух линиях (согласно вашему варианту);

- сохраните исходные данные, используя пиктограмму или команду File (Файл) → Save (Записать).

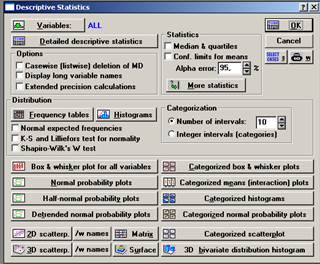
2. Вычислим дескриптивные (описательные) статистики выборок, относящихся к каждой из линий (см. табл. 2, табл. 3), посредством последовательного выполнения команд Analysis (Анализ) → Startup Panel (Стартовая панель) → Descriptive statistics (Описательные статистики) → Variables (Переменные) → Линия_№1 и Линия_№2 → More Statistics → Отметить знаком ˅ нужные статистики → OK (см. рис. 3, рис. 4, рис. 5).

→

Рисунок 3. Analysis → Startup Panel → Basic Statistics and Tables

→

Рисунок 4. Descriptive Statistics → More statistics → Statistics

Таблица 2. Таблица с описательными статистиками результатов замеров на 2-х линиях.

Прокручивая таблицу результатов слева направо, имеем следующие описательные статистики переменных:

Valid N – количество случаев переменной (количество строк);

Mean – выборочное среднее;

Confid -95% – нижняя граница 95% доверительного интервала для среднего;

Confid +95% – верхняя граница 95% доверительного интервала для среднего;

Sum – сумма значений переменной;

Minimum – минимальное значение переменной;

Maximum – максимальное значение переменной.

→

Рисунок 5. Descriptive Statistics → More statistics → Statistics

Таблица 3. Таблица с описательными статистиками результатов замеров на 2-х линиях.

Прокручивая таблицу результатов слева направо, имеем следующие описательные статистики переменных:

Range – разность между максимумом и минимумом (размах данных);

Variance – выборочная дисперсия;

Std.Dev. – стандартное отклонение;

Std.Err. – стандартная ошибка;

Skewness – выборочный коэффициент асимметрии;

Std.Err.Skewness – стандартная ошибка коэффициента асимметрии;

Kurtosis – выборочный коэффициент эксцесса;

Std.Err.Kurtosis – стандартная ошибка эксцесса.

3. Построим гистограммы выборочных распределений (см. рис. 8, рис. 10), посредством последовательного выполнения команд Graphs (Графики) → Stats 2D Graphs → Histograms → Variables (Переменные) → Линия_№1 затем Линия_№2 → Graph Type (Тип графика) → Regular → Fit Type → Normal или Off (Без подбора типа) → OK (см. рис. 6, рис. 7, рис. 9).

Рисунок 6. Graphs → Stats 2D Graphs → Histograms

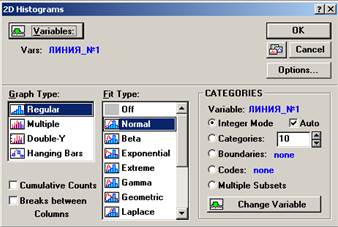
Рисунок 7. 2D Histograms

Рисунок 8. Гистограмма данных 1-ой линии

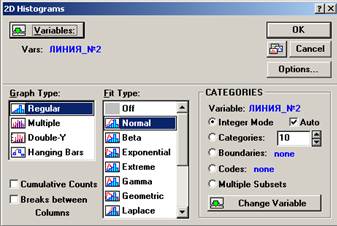
Рисунок 9. 2D Histograms

Рисунок 10. Гистограмма данных 2-ой линии

4. Построим вариационный ряд (см. рис. 12, рис. 14), посредством последовательного выполнения команд: Щелкнуть 1 раз мышью по имени переменной Линия_№1 затем по имени переменной Линия_№2 → Graphs (Графики) → Quick Stats Graphs (Быстрые статистики и графики) → Values/Stats of Линия_№1 (Значения и статистики Линии_№1) затем Values/Stats of Линия_№2 (Значения и статистики Линии_№2) → на экране появится вариационный ряд, выборочное среднее и стандартное отклонение (см. рис. 11, рис. 13).

→

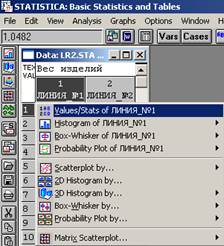
Рисунок 11. Graphs → Quick Stats Graphs → Values/Stats of Линия_№1

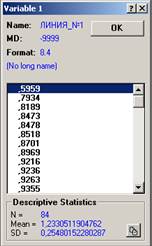
Рисунок 12. Вариационный ряд данных 1-ой линии

Рисунок 13. Values/Stats of Линия_№2

Рисунок 14. Вариационный ряд данных 2-ой линии

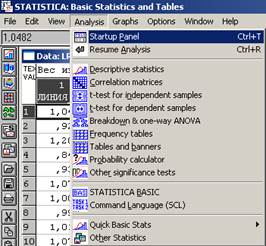
Построим интервальный ряд (см. табл. 4, табл. 5), посредством последовательного выполнения команд Analysis (Анализ) → Startup Panel (Стартовая панель) → Frequency tables → Variables (Переменные) → Линия_№1 затем Линия_№2 → No. of exact intervals (Интервалы группирования) → 7 → Display options → Cumulative frequencies (Накопленные частоты) → OK (см. рис. 15, рис. 16, рис. 17).

→

Рисунок 15. Analysis → Startup Panel → Basic Statistics and Tables

Рисунок 16. Frequency tables

Таблица 4. Таблица частот для данных первой линии.

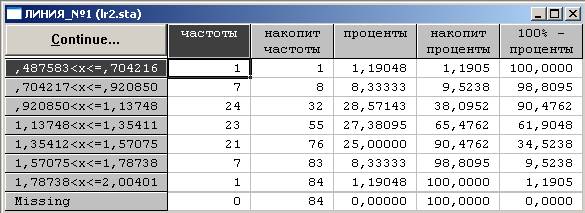
Рисунок 17. Frequency tables

Таблица 5. Таблица частот для данных второй линии.

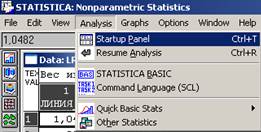
5. Используя критерии согласия, проверим гипотезы о законах распределения случайных величин (см. табл. 6, табл. 7), посредством последовательного выполнения команд: войдем в программу STATISTICA через модуль Nonparametric/Distrib. (Непараметрические статистики) (см. рис. 18) → File (Файл) → Open Data (Открыть данные) → Drivers (Диск) → h → File Name (Имя файла) → Ivanov1.STA → OK → Analysis (Анализ) → Startup Panel (Стартовая панель) → Distribution Fitting (Подбор распределения) → Continuous Distributions → Normal → OK → Variables (Переменные) → Линия_№1 затем Линия_№2 → Number of categories (Число групп) → 7 → Plot distribution → Frequency distribution (Частоты распределения) → OK → на экране появятся статистики Колмогорова-Смирнова и хи-квадрат критерий Пирсона (см. рис. 19, рис. 20, рис. 21).

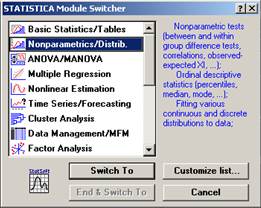
Рисунок 18. STATISTICA Module Switcher

→

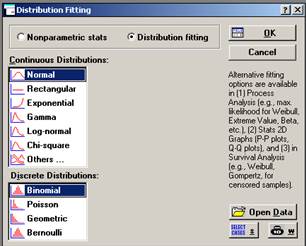
Рисунок 19. Analysis → Startup Panel → Distribution Fitting

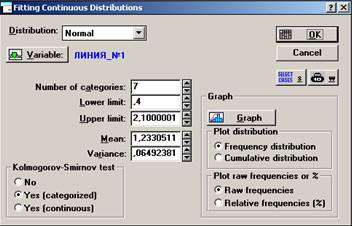
Рисунок 20. Fitting Continuous Distributions

Таблица 6. Результаты проверки на нормальность данных первой линии.

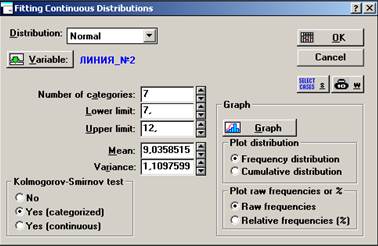
Рисунок 21. Fitting Continuous Distributions

Таблица 7. Результаты проверки на нормальность данных второй линии.

Найдем критическое значение Chi-Square (Хи-квадрат):

Найдем процент брака на Линии_№1, посредством последовательного выполнения команд Analysis (Анализ) → Startup Panel (Стартовая панель) → Probability calculator → Z(Normal) (Нормальное распределение) → mean (Выборочное среднее) → 1,233051 (см. табл. 2 на пересечении 2 столбца и 1 строки) → st.dev. (Стандартное отклонение) → 0,254802 (см. табл. 3 на пересечении 3 столбца и 1 строки) → Z → 1,3 (см. правую границу интервала в 1 абзаце 1 пункта данной лаб. работы) затем 1,1 (см. левую границу интервала в 1 абзаце 1 пункта данной лаб. работы) → Compute (Вычислить) (см. рис. 22, рис. 23, рис. 24).

→

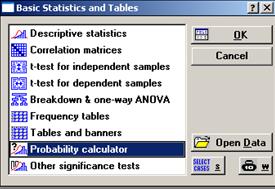
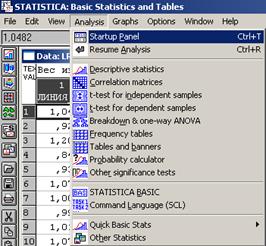
Рисунок 22. Analysis → Startup Panel → Basic Statistics and Tables

Рисунок 23. Probability Distribution Calculator

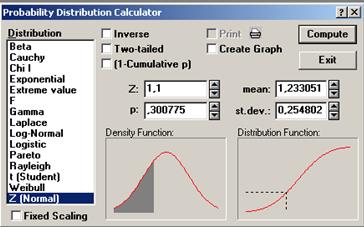
Рисунок 24. Probability Distribution Calculator

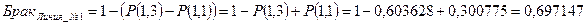
или

Найдем процент брака на Линии_№2, посредством последовательного выполнения команд Analysis (Анализ) → Startup Panel (Стартовая панель) → Probability calculator → Z(Normal) (Нормальное распределение) → mean (Выборочное среднее) → 9,035852 (см. табл. 2 на пересечении 2 столбца и 2 строки) → st.dev. (Стандартное отклонение) → 1,053451 (см. табл. 3 на пересечении 3 столбца и 2 строки) → Z → 1,3 (см. правую границу интервала в 1 абзаце 1 пункта данной лаб. работы) затем 1,1 (см. левую границу интервала в 1 абзаце 1 пункта данной лаб. работы) → Compute (Вычислить) (см. рис. 25, рис. 26, рис. 27).

→

Рисунок 25. Analysis → Startup Panel → Basic Statistics and Tables

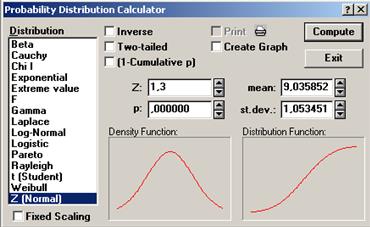
Рисунок 26. Probability Distribution Calculator

Рисунок 27. Probability Distribution Calculator

или

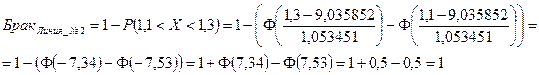
Полученные результаты по Линии_№1 не отвергают нулевую гипотезу, т.к. (см. табл. 6 ), а по Линии_№2 – отвергают, т.к. (см. табл. 7 ), что подтверждается гистограммами данных 1-ой и 2-ой линий (см. рис. 8 и рис. 10 соответственно).

Проведённый первичный анализ статистических данных позволяет сделать следующие выводы:

1. Поскольку представленные выборки не относятся к малым (), то для первичного анализа можно ограничиться точечными оценками. Средние значения для этих линий различаются (см. таблицу 2 столбец 2) на 5% уровне значимости (соответствующие доверительные интервалы не перекрываются – см. таблицу 2 столбцы 3 и 4), и первая линия имеет среднее ближе к стандарту, чем вторая (см. таблицу 2 столбец 2).

2. Сравнение среднеквадратичных отклонений выборочных данных показывает, что продукция, производимая на первой линии, отличается меньшим разбросом, чем на второй линии (см. таблицу 3 столбец 1). Принимая во внимание, что только первое распределение можно считать нормальным (т.к. нулевая гипотеза по Линии_№1 не отвергается, см. абзац перед выводом) и учитывая допуски, можно ожидать, что на первой линии брак составит примерно 69,71%, в то время как на второй – 100% (см. и соответственно).

Поэтому, при прочих равных условиях предпочтительнее приобрести первую линию.

Не нашли, что искали? Воспользуйтесь поиском: