
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Лабораторная работа №3. Задание к лабораторной работе №3
Задание к лабораторной работе №3
1. Проверить гипотезу о равенстве математических ожиданий 2-х выборок.
2. Проверить гипотезу о равенстве дисперсий 2-х выборок.
3. Указать интервал, в котором с 95% надёжностью может находиться отношение дисперсий этих выборок при условии их равенства.
4. Указать интервал, в котором с 95% надёжностью может находиться разность между математическими ожиданиями этих выборок, при условии их равенства.
5. Вычислить выборочный коэффициент корреляции для имеющихся данных и проверить его значимость.
6. Составьте отчет о проделанной работе с данными своего варианта.
Замечание. Предварительно следует вычислить точечные оценки рассматриваемых числовых характеристик и убедиться, что выполнены необходимые условия, при которых возможно проверить сформулированные выше гипотезы.
Лабораторная работа №3
В таблице 1 приведены данные 2-х выборок:
Таблица 1. Исходные данные.

Файл с этими данными создается по следующей схеме:
- осуществляется вход в программу STATISTICA через модуль Basic Statistics/Tables (см. рис. 1);

Рисунок 1. STATISTICA Module Switcher
- затем последовательно выполняются команды File (Файл) → New Data (Новые данные) → Drivers (Диск) → h → File Name (Имя файла) → Ivanov1.STA → OK;
- программа автоматически открывает пустую электронную таблицу с именем Ivanov1.STA;
- в таблице делается 4 столбца, посредством последовательного выполнения команд Vars (Переменные) → Delete (Удалить) → From Variables (От переменной) → Var 5 → To Variables (До переменной) → Var 10 → OK;
- в таблице делается 36 строк, посредством последовательного выполнения команд Cases (Случаи) → Add (Добавить) → Number of Cases to Add (Количество добавляемых случаев) → 26 → OK;
- дважды щелкните мышью по имени переменной VAR1 и в поле Name (Имя) напишите X1. То же сделайте для переменных VAR2, VAR3 и VAR4;
- для установки числа разрядов после десятичной точки равным 4 щелкните 1 раз мышью по имени переменной X1 и 1 раз по пиктограмме  . То же сделайте для переменных Y1, X2 и Y2;
. То же сделайте для переменных Y1, X2 и Y2;
- введите в полученную таблицу данные 2-х выборок (согласно вашему варианту);
- сохраните исходные данные, используя пиктограмму  или команду File (Файл) → Save (Записать).
или команду File (Файл) → Save (Записать).
Замечание. Для выполнения работы можно было создать файл с 2 переменными, например, V1 и V2, в которые были бы занесены данные каждой выборки. Однако при этом пришлось бы создавать ещё группирующую переменную с кодами переменных.
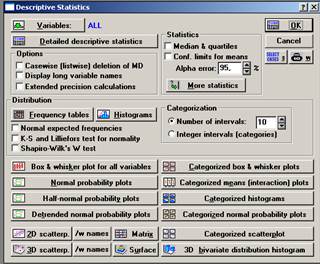
Вычислим дескриптивные (описательные) статистики выборок, относящихся к каждой из переменных (см. табл. 2, табл. 3), посредством последовательного выполнения команд Analysis (Анализ) → Startup Panel (Стартовая панель) → Descriptive statistics (Описательные статистики) → Variables (Переменные) → X1, Y1, X2 и Y2 → More Statistics → Отметить знаком ˅ нужные статистики → OK (см. рис. 2, рис. 3, рис. 4).
 →
→ 
Рисунок 2. Analysis → Startup Panel → Basic Statistics and Tables
 →
→ 
Рисунок 3. Descriptive Statistics → More statistics → Statistics
Таблица 2. Таблица с описательными статистиками данных 2-х выборок.

Прокручивая таблицу результатов слева направо, имеем следующие описательные статистики переменных:
Valid N – количество случаев переменной (количество строк);
Mean – выборочное среднее;
Confid -95% – нижняя граница 95% доверительного интервала для среднего;
Confid +95% – верхняя граница 95% доверительного интервала для среднего;
Minimum – минимальное значение переменной;
Maximum – максимальное значение переменной.
 →
→ 
Рисунок 4. Descriptive Statistics → More statistics → Statistics
Таблица 3. Таблица с описательными статистиками данных 2-х выборок.
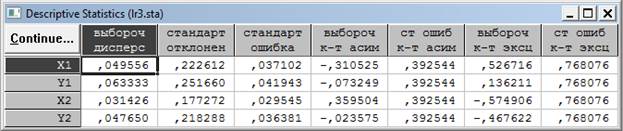
Прокручивая таблицу результатов слева направо, имеем следующие описательные статистики переменных:
Variance – выборочная дисперсия;
Std.Dev. – стандартное отклонение;
Std.Err. – стандартная ошибка;
Skewness – выборочный коэффициент асимметрии;
Std.Err.Skewness – стандартная ошибка коэффициента асимметрии;
Kurtosis – выборочный коэффициент эксцесса;
Std.Err.Kurtosis – стандартная ошибка эксцесса.
Построим гистограммы выборочных распределений (см. рис. 7, рис. 9, рис. 11, рис. 13), посредством последовательного выполнения команд Graphs (Графики) → Stats 2D Graphs → Histograms → Variables (Переменные) → X1, Y1, X2 и Y2 → Graph Type (Тип графика) → Regular → Fit Type → Normal или Off (Без подбора типа) → CATEGORIES → 8 → OK (см. рис. 5, рис. 6, рис. 8, рис. 10, рис. 12).
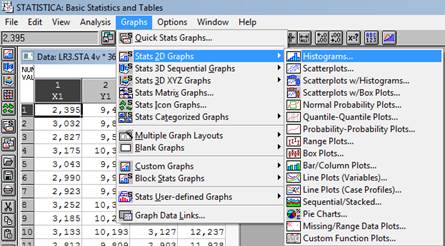
Рисунок 5. Graphs → Stats 2D Graphs → Histograms

Рисунок 6. 2D Histograms
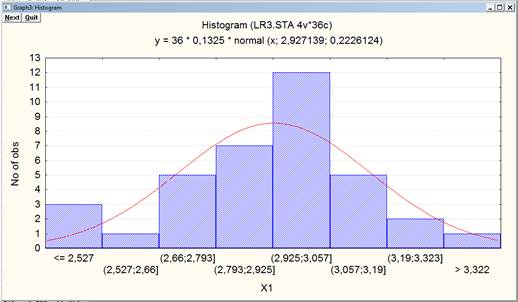
Рисунок 7. Гистограмма распределения признака X1

Рисунок 8. 2D Histograms

Рисунок 9. Гистограмма распределения признака Y1

Рисунок 10. 2D Histograms

Рисунок 11. Гистограмма распределения признака X2

Рисунок 12. 2D Histograms

Рисунок 13. Гистограмма распределения признака Y2
Поскольку объём выборки сравнительно невелик, то для проверки данных на нормальность используем критерий Колмогорова-Смирнова (см. табл. 4), посредством последовательного выполнения команд Analysis (Анализ) → Startup Panel (Стартовая панель) → Frequency tables → Variables (Переменные) → X1, Y1, X2 и Y2 → Tests of normality → K-S test, mean/std.dv known (тест Колмогорова-Смирнова) → Tests for normality (см. рис. 14, рис. 15).
 →
→ 
Рисунок 14. Analysis → Startup Panel → Basic Statistics and Tables

Рисунок 15. Frequency tables
Таблица 4. Тест Колмогорова-Смирнова проверки данных на нормальность.

Полученные значения уровней значимости ( ) (см. табл. 4) свидетельствуют о том, что имеющиеся данные не противоречат нулевой гипотезе для всех признаков. Поэтому в дальнейшем будем полагать, что выборочные данные взяты из генеральных совокупностей, имеющих нормальные распределения с соответствующими параметрами.
) (см. табл. 4) свидетельствуют о том, что имеющиеся данные не противоречат нулевой гипотезе для всех признаков. Поэтому в дальнейшем будем полагать, что выборочные данные взяты из генеральных совокупностей, имеющих нормальные распределения с соответствующими параметрами.
Результаты теста можно подтвердить путем построения графиков нормальной вероятности (см. рис. 18, рис. 20, рис. 22, рис. 24), посредством последовательного выполнения команд Analysis (Анализ) → Startup Panel (Стартовая панель) → Frequency tables → Variables (Переменные) → X1, Y1, X2 и Y2 → Normal probability plots (см. рис. 16, рис. 17, рис. 19, рис. 21, рис. 23).
 →
→ 
Рисунок 16. Analysis → Startup Panel → Basic Statistics and Tables

Рисунок 17. Frequency tables

Рисунок 18. График нормальной вероятности для переменной X1

Рисунок 19. Frequency tables

Рисунок 20. График нормальной вероятности для переменной Y1
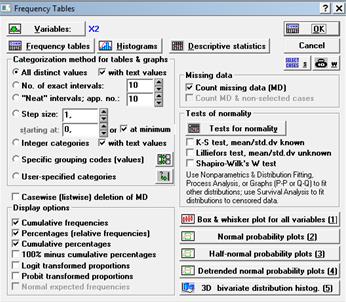
Рисунок 21. Frequency tables
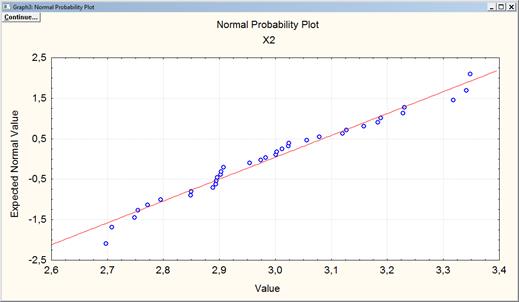
Рисунок 22. График нормальной вероятности для переменной X2

Рисунок 23. Frequency tables

Рисунок 24. График нормальной вероятности для переменной Y2
На графиках (см. рис. 18, рис. 20, рис. 22, рис. 24) можно видеть, что точки, соответствующие наблюдениям, достаточно близко расположены к прямым, поэтому распределения можно считать приближенно нормальными.
1-2. Проверим гипотезы о равенстве математических ожиданий и дисперсий (см. табл. 5), посредством последовательного выполнения команд Analysis (Анализ) → Startup Panel (Стартовая панель) → t-test for independent samples (t-критерий для независимых выборок) → Input file → Each variable contains the data for one group  (каждая переменная содержит данные одной выборки) → Variables (groups) [Переменные (выборки)] → First list → X1 → Second list → X2 → OK (см. рис. 25, рис. 26).
(каждая переменная содержит данные одной выборки) → Variables (groups) [Переменные (выборки)] → First list → X1 → Second list → X2 → OK (см. рис. 25, рис. 26).
 →
→ 
Рисунок 25. Analysis → Startup Panel → Basic Statistics and Tables
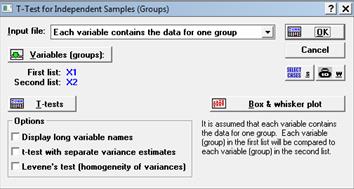
Рисунок 26. T-Test for Independent Samples (Groups)
Таблица 5. Результаты тестирования двух независимых выборок Х1 и Х2.


В таблице 5 для выборок X1 и X2 последовательно представлены: средние значения переменных ( и
и  ), расчётное значение t-критерия (
), расчётное значение t-критерия ( ), число степеней свободы критерия (
), число степеней свободы критерия (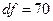 ) и уровень значимости нулевой гипотезы (
) и уровень значимости нулевой гипотезы ( ). Поскольку уровень значимости превышает 5%, то гипотезу о равенстве средних значений отклонять не следует.
). Поскольку уровень значимости превышает 5%, то гипотезу о равенстве средних значений отклонять не следует.
Во второй части таблицы 5 приводятся объёмы выборок ( ), стандартные отклонения (
), стандартные отклонения (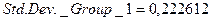 и
и  ), расчётное значение F-критерия (
), расчётное значение F-критерия ( ) и уровень значимости нулевой гипотезы (
) и уровень значимости нулевой гипотезы ( ). Как и в предыдущем случае, уровень значимости превышает стандартные 5%, и, следовательно, гипотезу о равенстве дисперсий следует принять.
). Как и в предыдущем случае, уровень значимости превышает стандартные 5%, и, следовательно, гипотезу о равенстве дисперсий следует принять.
Для визуального представления данных (см. рис. 30) выполним следующую последовательность команд: Analysis (Анализ) → Startup Panel (Стартовая панель) → t-test for independent samples (t-критерий для независимых выборок) → Input file → Each variable contains the data for one group  (каждая переменная содержит данные одной выборки) → Variables (groups) [Переменные (выборки)] → First list → X1 → Second list → X2 → Box & whisker plot (график “Ящик с усами” – так переводится название диаграммы размаха данных) → Mean/SE/SD (Выборочное среднее/Стандартная ошибка/Стандартное отклонение) → OK (см. рис. 27, рис. 28, рис. 29).
(каждая переменная содержит данные одной выборки) → Variables (groups) [Переменные (выборки)] → First list → X1 → Second list → X2 → Box & whisker plot (график “Ящик с усами” – так переводится название диаграммы размаха данных) → Mean/SE/SD (Выборочное среднее/Стандартная ошибка/Стандартное отклонение) → OK (см. рис. 27, рис. 28, рис. 29).
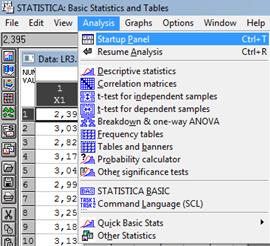 →
→ 
Рисунок 27. Analysis → Startup Panel → Basic Statistics and Tables

Рисунок 28. T-Test for Independent Samples (Groups)

Рисунок 29. Box-Whisker Type

Рисунок 30. Диаграмма размаха данных для переменных X1 и X2
Смысл этих графиков (см. рис. 30) следующий: точки в центре прямоугольников (ящиков) соответствуют средним значениям переменных X1 и X2. От этих значений откладывается положительное стандартное отклонение, отрицательное стандартное отклонение, положительная стандартная ошибка, отрицательная стандартная ошибка, т.о. получаются «усы» и «ящик». На графике видно, что среднее значение второй переменной больше, но интервалы стандартных отклонений перекрываются, следовательно, средние отличаются незначимо, что подтверждается данными таблицы 5.
Аналогичным образом проведём сравнение других переменных в выборке, например, X1 и Y1 (см. табл. 6). Поскольку эти переменные получены в результате измерений на одних и тех же объектах выборки, то их следует рассматривать как зависимые. В этом случае последовательность выполнения команд будет следующей: Analysis (Анализ) → Startup Panel (Стартовая панель) → t-test for dependent samples (t-критерий для зависимых выборок) → Variables (Переменные) → First list → X1 → Second list → Y1 → OK (см. рис. 31, рис. 32).
 →
→ 
Рисунок 31. Analysis → Startup Panel → Basic Statistics and Tables

Рисунок 32. T-Test for Dependent (Correlated) Samples
Таблица 6. Результаты тестирования двух зависимых выборок Х1 и Y1.

В таблице 6 приводятся следующие результаты сравнений: средние значения переменных, образующих выборки ( и
и  ), стандартные отклонения (
), стандартные отклонения ( и
и  ), число наблюдений в выборках (
), число наблюдений в выборках (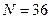 ), разность между средними значениями переменных (
), разность между средними значениями переменных (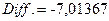 ), значение статистики t-критерия (
), значение статистики t-критерия ( ), число степеней свободы (
), число степеней свободы ( ) и уровень значимости нулевой гипотезы (
) и уровень значимости нулевой гипотезы ( ). Величина уровня значимости позволяет уверенно отвергнуть предположение о равенстве средних выборочных совокупностей, т.к.
). Величина уровня значимости позволяет уверенно отвергнуть предположение о равенстве средних выборочных совокупностей, т.к. 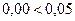 .
.
Замечание. Красным цветом выделяется содержание таблиц в случае значимого результата.
Для визуального представления данных (см. рис. 36) выполним следующую последовательность команд: Analysis (Анализ) → Startup Panel (Стартовая панель) → t-test for dependent samples (t-критерий для зависимых выборок) → Variables (Переменные) → First list → X1 → Second list → Y1 → Box & whisker plot (график “Ящик с усами” – так переводится название диаграммы размаха данных) → Mean/SE/SD (Выборочное среднее/Стандартная ошибка/Стандартное отклонение) → OK (см. рис. 33, рис. 34, рис. 35).
 →
→ 
Рисунок 33. Analysis → Startup Panel → Basic Statistics and Tables

Рисунок 34. T-Test for Dependent (Correlated) Samples

Рисунок 35. Box-Whisker Type

Рисунок 36. Диаграмма размаха данных для переменных X1 и Y1
Задание: Самостоятельно проверить гипотезы о равенстве средних и дисперсий для остальных пар выборок.
Проверку гипотез о равенстве дисперсий двух выборок можно провести, используя непосредственное вычисление F-критерия и последующее сравнение полученного значения с критическим. Покажем это на примере переменных Y1 и Y2.
Пусть основная гипотеза 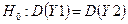 , а альтернативная –
, а альтернативная – 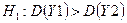 .
.
Для проверки основной гипотезы вычислим 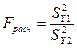 . Значения выборочных дисперсий составляют
. Значения выборочных дисперсий составляют  (см. табл. 3 на пересечении 1 столбца и 2 строки) и
(см. табл. 3 на пересечении 1 столбца и 2 строки) и  (см. табл. 3 на пересечении 1 столбца и 4 строки). В нашем случае
(см. табл. 3 на пересечении 1 столбца и 4 строки). В нашем случае  .
.
Найдем критическое значение F-критерия (см. рис. 38), посредством последовательного выполнения команд Analysis (Анализ) → Startup Panel (Стартовая панель) → Probability calculator → F (Распределение Фишера) →  (Число степеней свободы) → 35 (
(Число степеней свободы) → 35 (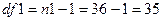 , где
, где  – объем выборки Y1) →
– объем выборки Y1) →  (Число степеней свободы) → 35 (
(Число степеней свободы) → 35 ( , где
, где  – объем выборки Y2) →
– объем выборки Y2) →  (Уровень надёжности) → 0,95 → Inverse → ˅ → Create Graph → ˅ → Compute (Вычислить) (см. рис. 37, рис. 38).
(Уровень надёжности) → 0,95 → Inverse → ˅ → Create Graph → ˅ → Compute (Вычислить) (см. рис. 37, рис. 38).
 →
→ 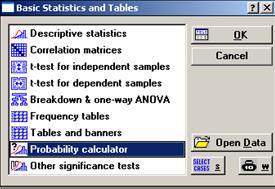
Рисунок 37. Analysis → Startup Panel → Basic Statistics and Tables

Рисунок 38. Probability Distribution Calculator

Рисунок 39. Probability Density Function
Т.о. критическое значение F-критерия составит – 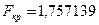 (см. рис. 38).
(см. рис. 38).
Поскольку  , то оснований для отвержения основной гипотезы
, то оснований для отвержения основной гипотезы 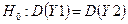 нет.
нет.
3. Найдем интервал, в котором с надежностью 95% может находиться отношение дисперсий данных выборок. Для этого с помощью вероятностного калькулятора построим доверительный интервал, границами которого являются квантили уровней 0,025 ( ) и 0,975 (
) и 0,975 (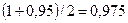 или
или  ) распределения Фишера с числом степеней свободы числителя 35 (
) распределения Фишера с числом степеней свободы числителя 35 (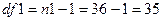 ) и знаменателя 35 (
) и знаменателя 35 ( ). В результате получим интервал
). В результате получим интервал  , т.к.
, т.к.  и
и  .
.
Нетрудно заметить, что этот интервал включает в себя значение единицы. В соответствие с принципом двойственности теории доверительных интервалов и проверки гипотез о значениях параметров приходим к выводу, что отношение двух дисперсий равно единице, т.е. гипотеза 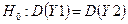 не противоречит имеющимся данным на уровне значимости 0,05.
не противоречит имеющимся данным на уровне значимости 0,05.
4. Найдем интервал, в котором с надежностью 95% может находиться разность между математическими ожиданиями данных выборок в предположении, что дисперсии равны, но неизвестны.
Определим с помощью вероятностного калькулятора границы доверительного интервала (см. рис. 41, рис. 42), посредством последовательного выполнения команд Analysis (Анализ) → Startup Panel (Стартовая панель) → Probability calculator → t (Student) (t-распределение Стьюдента) →  (Число степеней свободы) → 70 (
(Число степеней свободы) → 70 (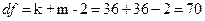 , где
, где  – объемы выборок Y1 и Y2) →
– объемы выборок Y1 и Y2) →  (Уровень надёжности) → 0,95 → Inverse → ˅ → Two-tailed (Двусторонняя критическая область) → ˅ → Create Graph → ˅ → Compute (Вычислить) (см. рис. 40, рис. 41).
(Уровень надёжности) → 0,95 → Inverse → ˅ → Two-tailed (Двусторонняя критическая область) → ˅ → Create Graph → ˅ → Compute (Вычислить) (см. рис. 40, рис. 41).
 →
→ 
Рисунок 40. Analysis → Startup Panel → Basic Statistics and Tables

Рисунок 41. Probability Distribution Calculator

Рисунок 42. Probability Density Function
Т.о. критическое значение t-критерия Стьюдента составит – 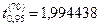 (см. рис. 41).
(см. рис. 41).
Полученный доверительный интервал  включает в себя нулевое значение. В соответствие с принципом двойственности теории доверительных интервалов и проверки гипотез о значениях параметров приходим к выводу, что разность двух средних значений в этих выборках равна нулю, т.е. гипотеза
включает в себя нулевое значение. В соответствие с принципом двойственности теории доверительных интервалов и проверки гипотез о значениях параметров приходим к выводу, что разность двух средних значений в этих выборках равна нулю, т.е. гипотеза  не противоречит имеющимся данным на уровне значимости 0,05.
не противоречит имеющимся данным на уровне значимости 0,05.
Задание: Самостоятельно проверить гипотезы о равенстве средних и дисперсий для остальных пар выборок.
5. Вычислим выборочные коэффициенты корреляции (см. табл. 7) для имеющихся данных и проверим их значимость, посредством последовательного выполнения команд Analysis (Анализ) → Startup Panel (Стартовая панель) → Correlation matrices (Корреляционные матрицы) → One variable list (square matrix) → First list → X1, Y1, X2 и Y2 → Second list → none → Display → Corr.matrix (display p&N) → OK (см. рис. 43, рис. 44).
 →
→ 
Рисунок 43. Analysis → Startup Panel → Basic Statistics and Tables

Рисунок 44. Pearson Product-Moment Correlation
Таблица 7. Матрица парных коэффициентов корреляции Пирсона.

В каждой ячейке матрицы приводятся значения коэффициентов корреляции и уровень значимости нулевой гипотезы (см. табл. 7). Красным цветом выделяются результаты значимые на уровне 5%. Так, например, на пересечении строки Х1 и столбца Y1 находится величина 0,9317, равная значению выборочного коэффициента. Ниже приводится уровень значимости нулевой гипотезы 
 при альтернативной гипотезе
при альтернативной гипотезе  . В нашем случае эта величина меньше 0,01. Как значение коэффициента корреляции, так и значение
. В нашем случае эта величина меньше 0,01. Как значение коэффициента корреляции, так и значение  уровня значимости выделены красным цветом. Это означает, что коэффициент корреляции значимо отличается от нуля.
уровня значимости выделены красным цветом. Это означает, что коэффициент корреляции значимо отличается от нуля.
В качестве другого примера рассмотрим выборочный коэффициент корреляции между переменными Х1 и Х2. Его величина равна –0,0234, а уровень значимости этого коэффициента составляет  . Вероятность ошибки первого рода, заключающаяся в отвержении нулевой гипотезы, весьма значительна, и, поэтому её не следует отвергать. Другими словами, следует признать, что переменные Х1 и Х2 не коррелируют друг с другом.
. Вероятность ошибки первого рода, заключающаяся в отвержении нулевой гипотезы, весьма значительна, и, поэтому её не следует отвергать. Другими словами, следует признать, что переменные Х1 и Х2 не коррелируют друг с другом.
Задание: Для остальных пар переменных самостоятельно проверьте гипотезы о значимости коэффициентов корреляции.
| <== предыдущая лекция | | | следующая лекция ==> |
| | |
Не нашли, что искали? Воспользуйтесь поиском: