Классической регрессии

Прежде, чем использовать построенную эконометрическую модель, важно определить, выполнялись ли предпосылки МНК, поскольку от этого зависит, обладают ли оценки параметров модели нужными свойствами. Особенно важно провести проверку на:

· гомоскедастичность – является ли дисперсия остатков постоянной;

· отсутствие автокорреляции остатков – остатки независимы;

· отсутствие мультиколлинеарности – некоррелированность объясняющих переменных.

Гетероскедастичность приводит к тому, что оценки параметров модели больше не представляют собой лучшие оценки, или не являются оценками с минимальной дисперсией, т.е. они не обладают свойством эффективности.

Воздействие гетероскедастичности на оценку интервала прогнозирования и проверку гипотезы заключается в том, что хотя коэффициенты не смещены, дисперсии, и, следовательно, стандартные ошибки этих коэффициентов будут смещены. Чаще всего смещение является отрицательным (т.е. в сторону уменьшения), значит, стандартные ошибки будут меньше, чем они должны быть, а t-критерий – больше, чем в реальности. Вследствие этого мы можем отвергнуть нулевую гипотезу, в то время как она должна быть принята, т.е. ошибочно будем считать коэффициент регрессии значимым, тогда как это не так.

Для проверки на гетероскедастичность используется тест Голдфельда-Квандта. При проведении проверки по этому критерию предполагается, что стандартное отклонение (s_i) распределения вероятностей e_i пропорционально значению Х в этом наблюдении. Предполагается также, что возмущение распределено нормально и не подвержено автокорреляции.

В соответствии с тестом Голдфельда-Квандта выполняем следующие действия:

1) все n наблюдений упорядочим по возрастанию Х;

2) отбросим с средних наблюдений; величину с предлагается определять так: ,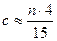

причем удобно принимать такое значение с, которое позволяет иметь два подмассива одинаковой длины m (после отбрасывания средних наблюдений);

3) оцениваем отдельные регрессии для первых m и для последних m наблюдений и находим суммы квадратов остатков в двух указанных регрессиях, которые обозначим S₁ и S_2, соответственно;

4) рассчитаем отношение F = S₂ /S₁, которое имеет F- распределение с n₁ = n₂ = m – (р + 1) степенями свободы, где р – число объясняющих переменных в регрессионном уравнении. Сравнив расчетное F с табличным, делаем вывод: о наличии гетероскедастичности, если F расчетное больше F табличного; о гомоскедастичности остатков – в противном случае.

Если в модели имеется более одной объясняющей переменной, то наблюдения следует упорядочивать по той из них, которая, как предполагается, связана с s_i.

Метод Голдфельда-Квандта можно применять и при предположении, что s_i обратно пропорционально значению Х. При этом используется та же процедура, но тестовой статистикой теперь является отношение F = S₁ /S₂.

Пример 2. В таблице 2 (столбцы 2, 3) приведены данные о величине сбережений (Y) и доходов (Х) соответственно для выборки из18 семей. Поскольку величина дохода сильно различается, следует выполнить проверку гетероскедастичности.

Данные табл. 2 уже упорядочены по возрастанию Х. В соответствии с тестом Голдфельда-Квандта из середины массива данных удаляем 18*4/15=4,8»4 точки и получаем 2 массива.

Таблица 2

№ наблюдения	Сбережения(Y)	Доход (Х)	Y расчетн.	Остатки (е)	Квадрат остатков (е2)
	2,3		2,16	2,3 –2,16=0,14	0,020
	2,2		2,16	2,2 – 2,16=0,04	0,002
	2,08		2,20	2,08 – 2,2=-0,12	0,015
	2,2		2,25	2,2 –2,25=-0,05	0,002
	2,1		2,25	2,1 –2,25=-0,15	0,022
	2,32		2,29	2,32 –2,29=0,03	0,001
	2,45		2,34	2,45 –2,34=0,11	0,012
	2,5				S1=0,07453
	2,2
	2,5
	3,1
	2,5		2,53	2,5 –2,53=-0,03	0,001
	2,82		2,68	2,82 –2,68=0,14	0,019
	3,04		2,99	3,04 –2,99=0,05	0,002
	2,7		3,18	2,7 –3,18=-0,48	0,234
	3,94		3,38	3,94 –3,38=0,56	0,318
	3,1		3,57	3,1 –3,57=-0,47	0,220
	3,99		3,76	3,99 –3,76=0,23	0,052
					S2=0,84581
F=	S2/S1=11,3483	> Fтабл.= 11
Таблица 3
№ набл.	Сбережен.	Доход
	Y	X	YX	X^2
	2,3		34,5
	2,2
	2,08		33,28
	2,2		37,4
	2,1		35,7
	2,32		41,76
	2,45		46,55
Сумма	15,65		262,19
7 b0 + 117 b1 = 15,65		b0=	1,475
117 b0 +1969 b1 = 262		b1=	0,045
Модель 1: Y^=1,475 + 0,045X
Таблица 4
	Y	X	YX	X^2
	2,5
	2,82		203,04
	3,04		243,2
	2,7		229,5
	3,94		354,6
	3,1		294,5
	3,99
Сумма	22,09		1893,84
7 b0 +590 b1 = 22,09		b0=	-0,093
590 b0 + 50558 b1 = 1894		b1=	0,038
Модель 2: Y^ = -0,093 + 0,038X

В таблицах 3 и 4 показан расчет оценок параметров моделей, которые строятся на основе полученных двух массивов, а в столбце 4 таблицы 2 представлены вычисленные по этим моделям значения исследуемого показателя Y (расчетные, или теоретические). Рассчитанное значение F-критерия больше табличного, выбранного при уровне значимости a = 5%, значит, гипотеза об отсутствии гетероскедастичности отвергается.

Поскольку остатки гетероскедастичны, метод наименьших квадратов для оценивания параметров модели применять нельзя.

Автокорреляция, также известная как сериальная корреляция, имеет место, когда остатки не являются независимыми друг от друга, потому что текущие значения Y находятся под влиянием прошлых значений. Зависимость между остатками описывается с помощью авторегрессионной схемы. Например, допустим, что остаток e_t находится под влиянием остатка из предыдущего периода времени e_{t -1} и какого-либо текущего значения случайной переменной u_t. Остаток e_t будет описываться следующей авторегрессионной функцией первого порядка:

.

Для проверки на автокорреляцию применяется критерий Дарбина-Уотсона, в соответствии с которым рассчитывается d-статистика (или DW):

.

Эмпирическое правило гласит, что если критерий Дарбина-Уотсона равен двум, то не существует автокорреляции, если он равен нулю, то имеет место совершенная положительная автокорреляция а если он равен четырем, то имеет место совершенная отрицательная автокорреляция. Авторы разработали таблицу, содержащую критические значения: нижнее d_L и верхнее d_u (или d_Н и d_В). Вычисленное значение d-статистики сравнивается с табличными, выбранными при заданном уровне значимости, в зависимости от количества наблюдений и числа независимых переменных в модели. Для d < 2 руководствуемся следующим правилом:

· если d < d_L, то имеется положительная автокорреляция;

· если d > d_u, то автокорреляции нет;

· если d_L < d < d_u, то ничего определенного сказать нельзя.

Если расчетное значение d больше двух, то описанной проверке подвергается величина (4 – d) и делаются те же выводы с той разницей, что автокорреляция будет отрицательной.

Автокорреляция может появиться из-за того, что не все важные факторы введены в модель, из-за неверно выбранной формы связи (уравнения регрессии). Введение переменных с лагом тоже может привести к автокорреляции остатков. Применение МНК для оценивания параметров модели при наличии автокорреляции имеет те же негативные последствия, как и в случае с гетероскедастичностью.

Пример 3. Проверим наличие автокорреляции остатков, используя условия примера 2. В табл. 5 выполнен расчет d-статистики Дарбина-Уотсона. Причем расчетные значения зависимой переменной, приведенные в 3-ем столбце таблицы, получены с использованием функции Excel ТЕНДЕНЦИЯ (о применении этой функции и других подробно рассказывается в следующем разделе).

Таблица 5

Y	Х	Y расчетн.	Остатки (е)
2,3		2,21607	0,08393		0,00704
2,2		2,21607	-0,01607	0,01	0,00026
2,08		2,23055	-0,15055	0,01808	0,02267
2,2		2,24503	-0,04503	0,01114	0,00203
2,1		2,24503	-0,14503	0,01	0,02103
2,32		2,2595	0,0605	0,04224	0,00366
2,45		2,27398	0,17602	0,01335	0,03098
2,5		2,28846	0,21154	0,00126	0,04475
2,2		2,28846	-0,08846	0,09	0,00782
2,5	22	2,31741	0,18259	0,07347	0,03334
3,1		2,92546	0,17454	6,5E-05	0,03046
2,5		2,98337	-0,48337	0,43284	0,23364
2,82		3,04128	-0,22128	0,06869	0,04896
3,04		3,15709	-0,11709	0,01085	0,01371
2,7		3,22948	-0,52948	0,17006	0,28035
3,94		3,30187	0,63813	1,36332	0,40721
3,1		3,37425	-0,27425	0,83245	0,07522
3,99		3,44664	0,54336	0,66849	0,29524
Сумма				3,81631	1,55134

. 4 – d = 4 – 2,46 = 1,54.

Из таблицы Дарбина-Уотсона при уровне значимости 0,05, задавшись количеством наблюдений n = 18 и числом независимых переменных к = 1, выбираем граничные значения:

d_L = 1,16, d_u = 1,39. Поскольку 4 – d = 1,54 > d_u = 1,39, то с вероятностью 0,95 можно утверждать, что автокорреляции остатков, полученных по модели, оцененной методом наименьших квадратов, не существует.

Мультиколлинеарность означает тесную линейную взаимосвязь между независимыми переменными модели. Если некоторые или все независимые переменные во множественной регрессии связаны сильной корреляционной зависимостью (мультиколлинеарны), то регрессионная модель не в состоянии разграничить их отдельные объясняющие воздействия на Y.

При мультиколлинеарности часто возникает противоречие между величиной и значимостью коэффициента детерминации и статистической надежностью коэффициентов регрессии. Так, значение коэффициента детерминации может быть высоким, и величина F-критерия подтверждает значимость коэффициента детерминации, следовательно, и уравнения регрессии в целом; в то же время стандартные ошибки оценок параметров модели высоки, и поэтому соответствующие t-статистики свидетельствуют о ненадежности этих коэффициентов.

Для выявления мультиколлинеарности можно использовать критерий Фаррара-Глобера, включающего следующие шаги.

1. Определение корреляционной матрицы объясняющих переменных R, элементами которой являются коэффициенты парной линейной корреляции между независимыми переменным. Построение корреляционной матрицы можно выполнить в Excel с помощью Пакета анализа (см. следующий раздел).

2. Определение критерия c²:

c² = – ,

где - определитель корреляционной матрицы R.

Полученное значение критерия c² сравнивается с табличным при 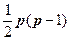степенях свободы и уровне значимости a. Если c²_факт > c²_табл, то в массиве независимых переменных существует мультиколлинеарность. (Табличные значения критерия c² можно найти в Excel.)

3. Вычисление обратной матрицы:

С = R^-1.

4. Расчет F-критериев:

,

где - диагональные элементы матрицы С.

Фактические значения критериев сравнивают с табличными значениями при n₁ = p – 1, n₂ = n – p степенях свободы и уровне значимости a. Если F_j > F_табл, то соответствующая i-я независимая переменная мультиколлинеарна с остальными. (Табличные значения критерия F можно найти в Excel.)

5. Определение частных коэффициентов корреляции:

,

где – элемент матрицы С, расположенный в j-й строке и к-м столбце; и - диагональные элементы матрицы С.

6. Вычисление t-критериев:

.

Фактические значения t-критериев сравнивают с табличными при n – p степенях свободы и уровне значимости a. Если , то между объясняющими переменными Х_k и X_j существует мультиколлинеарность. (Табличные значения критерия t можно найти в Excel.)

Пример применения алгоритма Фаррара-Глобера рассмотрим в следующем разделе.

Не нашли, что искали? Воспользуйтесь поиском: