ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Контрольной работы № 2
Для определения плотности теплового потока q, Вт/м2, через плоскую стенку и линейной плотности теплового потока ql = Вт/м через цилиндрическую стенку при известных температурах граничных поверхностей t 1ст и t n+1ст используются формулы, полученные на основании закона Фурье:
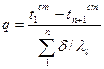 (1)
(1)
 , (2)
, (2)
где i = 1, 2, 3,…, n;
n – число отдельных слоев в стенке;
di – толщина каждого слоя стенки, м;
li – коэффициент теплопроводности каждого слоя, Вт/ (м´К).
Для сравнения линейной плоскости тепловых потоков при перемене мест тепловой изоляции трубы в задаче 4 можно воспользоваться приближенной формулой
 (3)
(3)
где 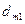 и
и  средние диаметры первого и второго цилиндрических слоев, м.
средние диаметры первого и второго цилиндрических слоев, м.
Относительное изменение линейной плоскости теплового потока при перемене слоев изоляции местами
 ∆
∆ 
В задачах 3,5,7 и 9 для расчета плотности теплового потока через плоскую стену можно использовать следующие формулы:
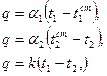
где  и
и  коэффициенты теплоотдачи со стороны горячей и холодной жидкости, омывающих стенку, Вт/(м2×К);
коэффициенты теплоотдачи со стороны горячей и холодной жидкости, омывающих стенку, Вт/(м2×К);
 и
и  температуры жидкостей, омывающих стенку;
температуры жидкостей, омывающих стенку;
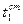 и
и  температуры поверхностей стенки со стороны горячей и холодной жидкостей;
температуры поверхностей стенки со стороны горячей и холодной жидкостей;
 коэффициент теплоотдачи, Вт/(м2×К);
коэффициент теплоотдачи, Вт/(м2×К);
 (7)
(7)
Для учета зависимости коэффициента теплопроводности материала стенки от ее температуры (задача 7) последней следует предварительно задаться. Например: 
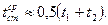
После определения коэффициента теплоотдачи (7) и плотности теплового потока по уравнению (6) найти температуру поверхностей стенок из уравнений (4) и (5) и проверить значение средней температуры стенки. В случае существенного расхождения расчет следует повторить.
Расчетная формула для определения линейной плотности теплового потока q1 через многослойную цилиндрическую стенку (задачи 2 и 6) базируется на основе совместного решения уравнений теплоотдачи (8) и (9) и теплопроводности (2):
 (8)
(8)
 (9)
(9)
Исключая неизвестные величины 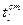 , получим:
, получим:
 (10)
(10)
где  число слоев в цилиндрической стенке.
число слоев в цилиндрической стенке.
Для нахождений толщины слоя изоляции трубы в задаче 8 следует сначала определить линейную плотность теплового потока (по заданным величинам  и
и  ) и требуемое термическое сопротивление изоляции (см. формулу 2):
) и требуемое термическое сопротивление изоляции (см. формулу 2):
 (11)
(11)
Линейная плотность теплового потока  и ток
и ток  в электрическом проводе (задача 10) могут быть найдены из уравнения теплового баланса:
в электрическом проводе (задача 10) могут быть найдены из уравнения теплового баланса:
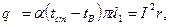 (12)
(12)
где  активное электрическое сопротивление провода, Ом/м.
активное электрическое сопротивление провода, Ом/м.
Для определения искомой температуры поверхности  изолированного провода при том же значении тока, т.е. при
изолированного провода при том же значении тока, т.е. при  , следует воспользоваться формулой (2) при
, следует воспользоваться формулой (2) при  , предварительно найдя температуру наружной поверхности изоляции
, предварительно найдя температуру наружной поверхности изоляции  из уравнения:
из уравнения:
 . (13)
. (13)
Максимальный ток определяется по предельно-допустимой температуре  из уравнения:
из уравнения:
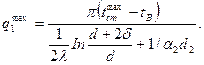
 (14)
(14)
Требуемые значения кинематического коэффициента вязкости 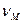 и скорости
и скорости 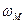 течение жидкости в модели (задача 11)определяются из условия подобия процессов в модели и образце, а именно из условия равенства критериев
течение жидкости в модели (задача 11)определяются из условия подобия процессов в модели и образце, а именно из условия равенства критериев  и
и 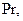 т.е.
т.е.

Для нахождения значений коэффициентов конвективной теплоотдачи в задачах 12,13,14,15,16 и 18 рекомендуется воспользоваться формулами, приведенными в контрольных вопросах 9-12. В формулах индекс «ж» указывает, что величины отнесены к определяющей температуре  т.е. средней температуре жидкости (среды).
т.е. средней температуре жидкости (среды).
Средний коэффициент теплоотдачи, Вт/(м2×К), при пленочной конденсации пара на поверхности горизонтальной трубы может быть определен по зависимости 8-3 [5] или по формуле
 (15)
(15)
где 

 теплота парообразования (конденсации), кДж/кг.
теплота парообразования (конденсации), кДж/кг.
Значения коэффициента теплопроводности  , плотности
, плотности  и коэффициент кинематической вязкости конденсата
и коэффициент кинематической вязкости конденсата  здесь отнесены к средней температуре
здесь отнесены к средней температуре  .
.
Температура насыщения  определяется по заданному давлению пара из таблиц насыщенного водяного пара. Из этих же таблиц находят значение теплоты парообразования.
определяется по заданному давлению пара из таблиц насыщенного водяного пара. Из этих же таблиц находят значение теплоты парообразования.
Для нахождения коэффициента теплоотдачи конвекцией в условиях абсолютного движения воздуха около горизонтальной трубы (задача 18) следует использовать критериальную формулу, приведенную в вопросе 12. Тепловой поток излучением может быть найден по закону Стефана-Больцмана
 (16)
(16)
где  коэффициент излучения абсолютно черного тела, Вт/(м2×К4).
коэффициент излучения абсолютно черного тела, Вт/(м2×К4).
Коэффициент теплоотдачи излучением
 (17)
(17)
Потери тепла излучением от циклической поверхности  , окруженной цилиндрическим экраном
, окруженной цилиндрическим экраном 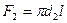 (задача 20), можно найти, определив предварительно температуру экрана
(задача 20), можно найти, определив предварительно температуру экрана 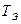 , из уравнения теплового баланса
, из уравнения теплового баланса 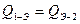 , т.е.
, т.е.
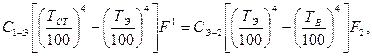 (18)
(18)
где 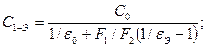

Для нахождения действительной температуры потока по показанию термометра (задача 21) следует использовать уравнение теплового баланса в виде
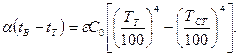 (19)
(19)
Температура изучающей поверхности (задача 22) может быть найдена из уравнения (16).
Задачи 22,23,24 и 25, связанные с тепловым расчетом рекуперативных теплообменников, решаются на основе использования уравнения теплового баланса
 (20)
(20)
и уравнения теплопередачи
 (21)
(21)
где 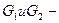 расходы греющего и нагреваемого теплоносителя, кг/с;
расходы греющего и нагреваемого теплоносителя, кг/с;
 и
и 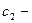 средние массовые теплоемкости теплоносителей в интервалах температур соответственно
средние массовые теплоемкости теплоносителей в интервалах температур соответственно  и
и  , кДж/(кг×К);
, кДж/(кг×К);
 и
и  температуры греющего и нагреваемого теплоносителей на входе в теплообменник;
температуры греющего и нагреваемого теплоносителей на входе в теплообменник;
 и
и 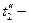 температуры греющего и нагреваемого теплоносителей на выходе из теплообменника;
температуры греющего и нагреваемого теплоносителей на выходе из теплообменника;
 коэффициент теплоотдачи, (кВт/м2×К);
коэффициент теплоотдачи, (кВт/м2×К);
 площадь теплообменной поверхности, м2;
площадь теплообменной поверхности, м2;
 средний температурный напор.
средний температурный напор.
При прямотоке и противотоке

где 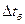 и
и 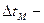 соответственно наибольшая и наименьшая разности температур теплоносителей в теплообменнике.
соответственно наибольшая и наименьшая разности температур теплоносителей в теплообменнике.
Если 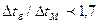 , то с достаточной для практических расчетов точностью
, то с достаточной для практических расчетов точностью
 .
.
Примеры решения задач контрольной работы № 1
Задача 1
До какой температуры будет нагрет углекислый газ  объемом объемом  , если сообщить ему теплоту Q при постоянном, абсолютном давлении? Начальная температура газа , если сообщить ему теплоту Q при постоянном, абсолютном давлении? Начальная температура газа  . Определить объем газа в конце процесса, а также удельные значения изменения внутренней энергии, энтальпии и энтропии в процессе. Теплоемкость принять не зависящей от температуры.
Дано: . Определить объем газа в конце процесса, а также удельные значения изменения внутренней энергии, энтальпии и энтропии в процессе. Теплоемкость принять не зависящей от температуры.
Дано:
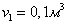

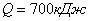 Решение:
Определяем температуру газа в конце процесса по формуле для количества теплоты в данном процессе:
Решение:
Определяем температуру газа в конце процесса по формуле для количества теплоты в данном процессе:
 где:
где:  - объем газа при нормальных условиях. - объем газа при нормальных условиях.
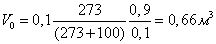
 - молярная теплоемкость газа - молярная теплоемкость газа

 - молярная теплоемкость для двухатомного газа - молярная теплоемкость для двухатомного газа
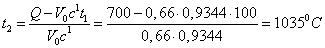 Найдем объем газа в конце процесса при р=const:
Найдем объем газа в конце процесса при р=const:

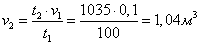 Определяем работу расширения газа в процессе:
Определяем работу расширения газа в процессе:
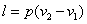
 Определяем изменение внутренней энергии процесса:
Определяем изменение внутренней энергии процесса:

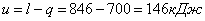 Определяем изменение энтальпии
Определяем изменение энтальпии
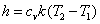
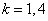 показатель адиабаты для двухатомных газов показатель адиабаты для двухатомных газов
 Определяем изменение энтропии
Определяем изменение энтропии
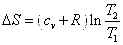
 Задача 2
Определить теоретическую скорость адиабатического истечения и массовый расход воздуха из сужающегося сопла площадью выходного сечения
Задача 2
Определить теоретическую скорость адиабатического истечения и массовый расход воздуха из сужающегося сопла площадью выходного сечения 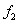 , если абсолютное давление перед соплом , если абсолютное давление перед соплом  , а давление среды в которую вытекает воздух , а давление среды в которую вытекает воздух  . Температура воздуха перед соплом . Температура воздуха перед соплом  . Скорость воздуха на входе в сопло и потерями на трение пренебречь. Будет ли полное расширение в сопле, если при прочих равных условиях давление за соплом понизится до 400 кПа? Как при этом изменится расход и скорость истечения воздуха?
Дано: . Скорость воздуха на входе в сопло и потерями на трение пренебречь. Будет ли полное расширение в сопле, если при прочих равных условиях давление за соплом понизится до 400 кПа? Как при этом изменится расход и скорость истечения воздуха?
Дано:

 МПа МПа
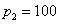 МПа
Решение:
Записываем уравнение неразрывности: МПа
Решение:
Записываем уравнение неразрывности:

 - массовый расход газа, кг/с; - массовый расход газа, кг/с;
 - скорость потока в рассматриваемом сечении, м/с. - скорость потока в рассматриваемом сечении, м/с.
 Так как
Так как
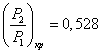 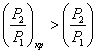 применяем формулу:
применяем формулу:

 м/с. м/с.
 кг/с
при понижении давление за до 400 кПа кг/с
при понижении давление за до 400 кПа
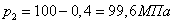
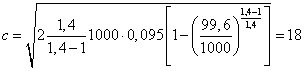
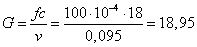 кг/с
Расход и скорость газа в сопле увеличились
Задача 3
Влажный насыщенный водяной пар с начальным параметром кг/с
Расход и скорость газа в сопле увеличились
Задача 3
Влажный насыщенный водяной пар с начальным параметром  , ,  дросселируется до давления дросселируется до давления  . Определить состояние пара в конце процесса дросселирования и его конечные параметры, а также изменение его внутренней энергии и энтропии. Условно изобразить процесс дросселирования на h-s диаграмме.
Дано: . Определить состояние пара в конце процесса дросселирования и его конечные параметры, а также изменение его внутренней энергии и энтропии. Условно изобразить процесс дросселирования на h-s диаграмме.
Дано:

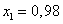
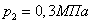 Решение:
Используем для определения конечных параметров h-s диаграмму
Таблица - Результаты расчета с помощью h – s диаграммы
Решение:
Используем для определения конечных параметров h-s диаграмму
Таблица - Результаты расчета с помощью h – s диаграммы
Определяем изменение внутренней энергии
Вычисляем изменение энтропии
|
Задача 4
Одноступенчатый поршневой компрессор всасывает воздух в количестве V при давлении  и
и  и сжимает его до давления по манометру
и сжимает его до давления по манометру  . Определить секундную работу сжатия и теоретическую мощность привода компрессора для случаев изотермического, адиабатного и политропного процессов (с показателем политропы n = 1,2) сжатия. Определить температуру воздуха в конце адиабатного и политропного сжатия. Сделать вывод по данным процесса.
. Определить секундную работу сжатия и теоретическую мощность привода компрессора для случаев изотермического, адиабатного и политропного процессов (с показателем политропы n = 1,2) сжатия. Определить температуру воздуха в конце адиабатного и политропного сжатия. Сделать вывод по данным процесса.
Дано:

 МПа
МПа
Решение:
а) изотермический процесс

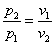
Работа изотермического процесса:

Мощность:

 Вт
Вт
б) адиабатный  при к = 1,4
при к = 1,4
Определяем температуру в конце сжатия


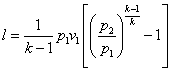


Мощность:
 Вт
Вт
в) политропный процесс n = 1,2



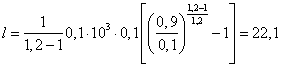

Мощность:
 Вт
Вт
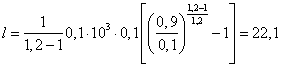

Вывод: наибольшей работой сжатия при данных условиях обладает газ в изотермическом процессе и, соответственно, он будет наиболее выгодный.
Не нашли, что искали? Воспользуйтесь поиском: