ТОР 5 статей:

Методические подходы к анализу финансового состояния предприятия

Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века

Ценовые и неценовые факторы

Характеристика шлифовальных кругов и ее маркировка

Служебные части речи. Предлог. Союз. Частицы

КАТЕГОРИИ:

Каждая координата середины отрезка равна полу сумме соответствующих координат ;

12 Следующая ⇒

Или бесконечно много

100) В пространстве даны две параллельные прямые a и b. Сколько существует плоскостей, проходящих через прямую a и параллельных прямой b?

Бесконечно много

101) В пространстве даны прямая a и точка M. Сколько существует плоскостей, проходящих через M и перпендикулярных прямой a?

Ответ

102) Известно, что прямая a параллельна прямой b, а прямая b пересекается с плоскостью γ. Каково взаимное расположение прямой a и плоскости γ?

Обязательно пересекаются

103) Даны три параллельные плоскости α, β, γ. Расстояние между α и β равно 3, расстояние между β и γ равно 5. Чему равно расстояние между плоскостями α и γ?

Или 8

Найти сумму элементов 3 столбца матрицы В.

15) . Найти . ответ

16) Найти сумму элементов 2 строки матрицы , если - ответ

17) 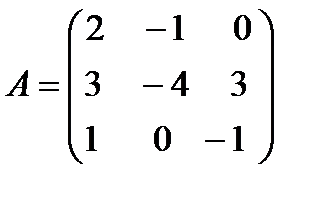, А+В -?

ответ

18) , . А-В -?

ответ

19) , . А*В -?

ответ

20) , 36

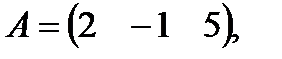
21) . А*В-?

Матрицы не умножается. либо

22) Решить систему уравнений

x₁=0, x₂=10, x₃=-1.

23) Решить систему уравнений методом Гаусса (исключения неизвестных)

x= 1, y= -3, z = - 1 .

24) Решить систему уравнений

x₁=1, x₂=-1, x₃=3. – правильный ответ, ни один из вариантов не подходит

25) Решить систему уравнений

x= 1, y= -1, z = 2.

26) Решить систему уравнений

x= 3, y= 2, z = 0.

28) Выберите верное утверждение.

каждая координата середины отрезка равна полу сумме соответствующих координат;

29) Даны точки А(5; 3; 2), В(3; - 1; - 4). Найдите длину вектора АВ.

2√14;

30) Даны точки А(- 1; 2; 3) и В (1; - 1; 4). Разложите вектор АВ по координатным векторам. AB = 2 i – 3 j + k;.

31) Выберите неверное утверждение.

если вектор а имеет координаты а{m; n; p}, то его разложение по координатным векторам будет таким: а = ni + pj + mk;

32) Из предложенных векторов выберите некомпланарные векторы.

а{1;-1;2}, b{-2;0;1},с{5;-1;0};

33) , . Найти 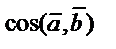16/17

34) Определить , при котором компланарны векторы , , .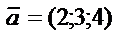

1/6

35) Составить уравнение плоскости, проходящей через точки , , .

6x+ 8y - 11z - 35=0

36) Известно, что , , а угол между и равен . Найти .

ответ

37) Уравнение прямой, проходящей через точки и , имеет вид:

ответ

38) Найти расстояние от точки до плоскости . (1)

39) Вычислить 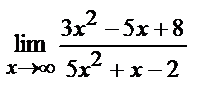ответ

40) Вычислить ответ

41) Вычислить ( 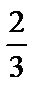ответ)

42) Вычислить ( ответ)

43) Вычислить (6)

44) Вычислить ( ответ)

45) Вычислить e^{4 ответ}

59) Найти указанный предел. 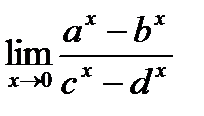( ответ)

60) Найти указанный предел. (2 - ответ)

61) Найти указанный предел. ( - ответ)

62) Найти указанный предел. (2 – ответ)

63) Найти указанный предел . (1 – ответ)

46) Найти производные функции:

7x⁶-x⁴+8x³-12x²+4x+3

47) Найти производные функции: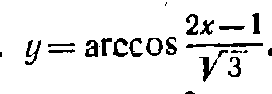

ответ. А правильнее

48) Найти производные функции:

ответ

49) Найти производные функции: ответ

50) Найти производные функции:

ответ

51) Найти производные от у по х. 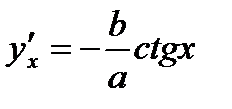ответ

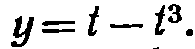
52) Найти производные от у по х. ответ

53) Найти производные от у по х.

ответ

54)

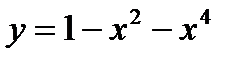
ответ. А правильнее

55) ответ

56)

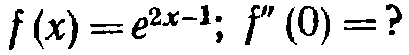
Или а правильный ответ

57) , а-const.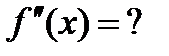

ответ

58) ;

ответ

64) Найти частное производное функции . ответ)

65) Найти частное производное функции

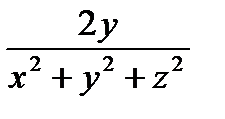ответ

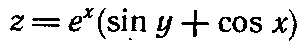
66) Найти частное производное функции ответ

67) Найти частное производное функции второго порядка

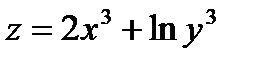
ответ

68) Найти частное производное функции 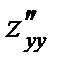второго порядка

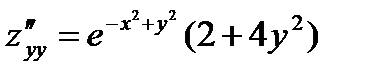ответ

69) Найти частное производное функции 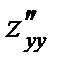второго порядка

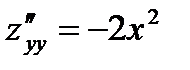ответ

70) Вычислите интеграл (30 – ответ)

71) Вычислите интеграл (0,5- ответ)

72) Неопределенным интегралом от функции называется

первообразная функции .

73) Вычислите интеграл: ( ответ)

74) Какая из данных функций является первообразной для функции y=2x³–3x²?

0,5 x⁴-x³+c ответ

75) Вычислить интеграл методом непосредственного интегрирования.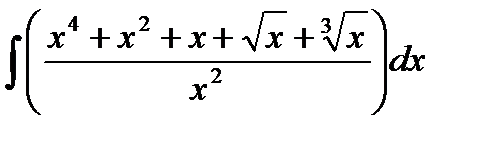

ответ

76) Вычислить интеграл методом непосредственного интегрирования .

ответ

77) Вычислить интеграл методом подстановки

ответ

78) Вычислить интеграл методом подстановки

ответ

79) Вычислить интеграл методом подстановки

ответ

80) Вычислить интеграл методом подстановки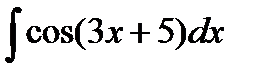

ответ

81) Вычислить интеграл методом интегрирование по частям

ответ

82) Вычислить интеграл методом интегрирование по частям

ответ

83) Вычислить интеграл методом интегрирование по частям

ответ

84) Вычислить интеграл методом интегрирование по частям

ответ

85) Вычислить интеграл методом непосредственного интегрирования.

ответ

86) Найти производные функции:

ответ

87) Найти производные функции:

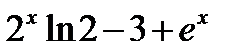ответ

88) Найти производные функции:

ответ

89) Найти производные функции:

1) ответ

90) Даны точки А(1; 3; 2), В(2; - 5; - 4). Найдите длину вектора АВ.

Правильный ответ ; ни одного верного варианта

91) Даны точки А(1; 4; 5) и В (1; - 1; 4). Разложите вектор АВ по координатным векторам.

АВ = 0 i - 5 j – k;

92) Даны векторы а {4; x² – y²; 3}, b {4; 15; x + y }. Найдите х и у, если a = b.

х = 4, у = - 1; ответ

93) Даны точки А(3; - 2; 4), В(4; - 1; 2), С(6; - 3; 2), D (7;- 3; 1). Найдите угол между векторами АВ и CD.

Ответ

94) Если функция стремится к нулю при , то функция стремится к...

12 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском: