ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
V3: {{101}} 04.07.14. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами (общее решение)
I:{{1016}} Э,С; t=0; k=5; ek=0; m=0; c=0;
S: Указать вид общего решения дифференциального уравнения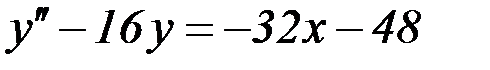 
, если частным решением является функция 
+: 
-: 
-: 
-: 
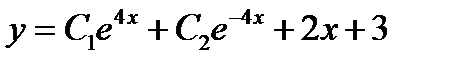
I:{{1017}} Э,С; t=0; k=5; ek=0; m=0; c=0;
S: Указать вид общего решения дифференциального уравнения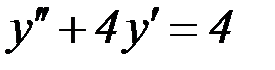 
, если частным решением является функция 
-: 
+: 
-: 
-: 
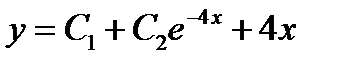
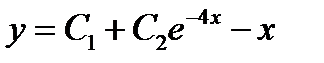
I:{{1018}} Э,С; t=0; k=5; ek=0; m=0; c=0;
S: Указать вид общего решения дифференциального уравнения 
, если частным решением является функция 
-: 
+: 
-: 
-: 
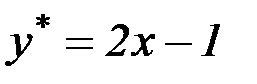
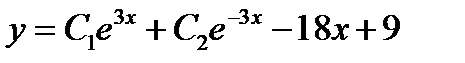
I:{{1019}} Э,С; t=0; k=5; ek=0; m=0; c=0;
S: Указать вид общего решения дифференциального уравнения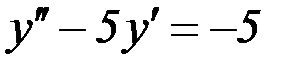 
, если частным решением является функция 
-: 
-: 
+: 
-: 
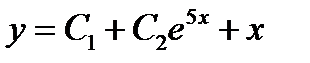
I:{{1020}} Э,С; t=0; k=5; ek=0; m=0; c=0;
S: Указать вид общего решения дифференциального уравнения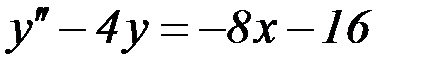 
, если частным решением является функция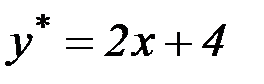 
-: 
+: 
-: 
-: 
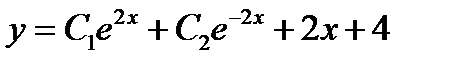
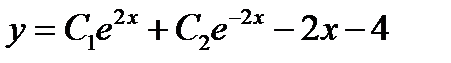
I:{{1021}} Э,С; t=0; k=5; ek=0; m=0; c=0;
S: ОБЪЕКТ НЕ ВСТАВЛЕН! Не удается открыть файл с помощью специального имени-: 
-: 
+: 
-: 
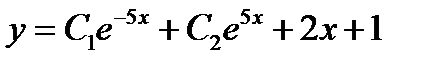
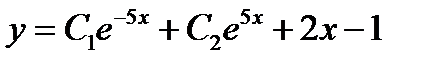
I:{{1022}} Э,С; t=0; k=5; ek=0; m=0; c=0;
S: Указать вид общего решения дифференциального уравнения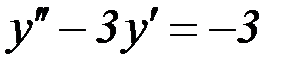 
, если частным решением является функция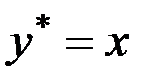 
-: 
+: 
-: 
-: 
I:{{1023}} Э,С; t=0; k=5; ek=0; m=0; c=0;
S: Указать вид общего решения дифференциального уравнения 
, если частным решением является функция 
-: 
-: 
-: 
+: 
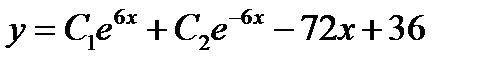
I:{{1024}} Э,С; t=0; k=5; ek=0; m=0; c=0;
S: Указать вид общего решения дифференциального уравнения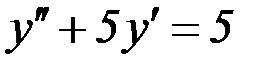 
, если частным решением является функция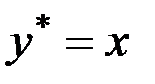 
+: 
-: 
-: 
-: 
I:{{1025}} Э,С; t=0; k=5; ek=0; m=0; c=0;
S: Указать вид общего решения дифференциального уравнения 
, если частным решением является функция 
-: 
-: 
+: 
-: 
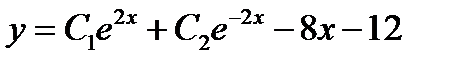
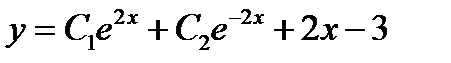
Не нашли, что искали? Воспользуйтесь поиском: