
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Действия над векторами.
Сложение. Сложение производится по правилу треугольника или правилу параллелограмма.
Вычитание. Операция вычитания сводится к сложению первого вектора и вектора, противоположного второму.
Скалярное произведение. Скалярное произведение вводится, как произведение двух векторов умножить на косинус угла между ними.
Векторное произведение. Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям: длина вектора c равна произведению длин векторов a и b на синус угла между ними, вектор c ортогонален каждому из векторов a и b, вектор c направлен так, что тройка векторов abc является правой.
Смешанное произведение. Смешанное произведение векторов abc – скалярное произведение вектора a на векторное произведение векторов b и c.
5. Линейные операции над векторами, заданными в координатной форме.
Равенство векторов и линейные операции (сложение векторов и умножение вектора на число) удобно представлять в координатной форме. При этом справедливы следующие свойства.
1. Равные векторы имеют равные координаты (в одном и том же базисе).
2. Каждая координата суммы векторов равна сумме соответствующих координат слагаемых.
3. Каждая координата произведения вектора на число равна произведению этого числа на соответствующую координату вектора.
4. Каждая координата линейной комбинации векторов равна линейной комбинации соответствующих координат векторов.
6. Коллиниарность и компланарность векторов.
Коллиниарность – отношение параллельности векторов: два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).
Компланарность. Компланарными называются векторы, которые лежат в одной плоскости, будучи приведенные к общему началу.
7. Скалярное, векторное, смешанное произведение векторов, определения, свойства, геометрический смысл векторного и скалярного произведений.
Скалярное произведение. Скалярное произведение вводится, как произведение двух векторов умножить на косинус угла между ними.
Векторное произведение. Векторным произведением вектора a на вектор b называется вектор c, удовлетворяющий следующим требованиям: длина вектора c равна произведению длин векторов a и b на синус угла между ними, вектор c ортогонален каждому из векторов a и b, вектор c направлен так, что тройка векторов abc является правой.
Смешанное произведение. Смешанное произведение векторов abc – скалярное произведение вектора a на векторное произведение векторов b и c.
скалярное произведение ненулевых векторов 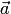 и
и 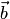 равно произведению длины вектора
равно произведению длины вектора  на алгебраическое значение длины ортогональной проекции вектора
на алгебраическое значение длины ортогональной проекции вектора  на ось, задаваемую вектором
на ось, задаваемую вектором 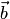 :
:
длина векторного произведения векторов 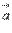 и
и  равна площади параллелограмма со сторонами
равна площади параллелограмма со сторонами 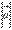 и
и 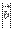 и углом между ними, равным
и углом между ними, равным 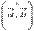 . В этом состоит геометрический смысл векторного произведения.
. В этом состоит геометрический смысл векторного произведения.
8. Уравнения прямой на плоскости: с угловым коэффициентом; через две точки; в отрезках, общее уравнение. 1. С угловым коэффициентом. 2. Через 2 точки. 3.Общее уравнение. 4. В отрезках.
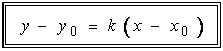
|
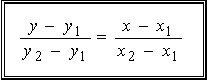
Ax+By+C=0 – общее уравнение
 , где a и b - некоторые отличные от нуля действительные числа.
, где a и b - некоторые отличные от нуля действительные числа.
9. Уравнение плоскости в векторной и координатной формах.
10. Уравнение плоскости и прямой в пространстве.
11. Расстояние от точки до плоскости.
Пусть плоскость  задана уравнением
задана уравнением 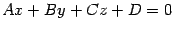 и дана точка
и дана точка  . Тогда расстояние
. Тогда расстояние 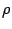 от точки
от точки 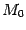 до плоскости
до плоскости  определяется по формуле
определяется по формуле
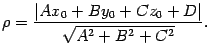
|
12. Условие параллельности и перпендикулярности векторов.
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов  .
.
Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны:
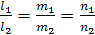 – условие параллельности прямых.
– условие параллельности прямых.
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:
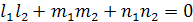 – условие перпендикулярности прямых.
– условие перпендикулярности прямых.
13. Канонические уравнения кривых второго порядка: формулы, определения, чертеж.
14. Предел числовой последовательности.
Предел числовой последовательности – предел последовательности элементов числового пространства. Числовое пространство – это метрическое пространство, расстояние в котором определяется как модуль разности между элементами.
15. Предел функции, его геометрическая интерпретация, действия над пределами.
Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, – такая величина, к которой стремится рассматриваемая функция при стремлении ее аргумента к данной точке.
16. Первый и второй замечательные пределы.
Первый замечательный предел. Предел, при x стремящийся к нулю синус x на x равен 1.
Второй замечательный предел. Предел, при x стремящийся к бесконечности 1 + 1/x все в степени x равно e.
17. Бесконечно малые величины, их свойства, эквивалентность.
Бесконечно малая величина – числовая функция или последовательность, которая стремится к нулю.
Свойства бесконечно малых величин.
Сумма (разность) бесконечно малых величин есть величина бесконечно малая.
Произведение бесконечно малых величин есть величина бесконечно малая.
Произведение бесконечно малой величины на константу C или на функцию, имеющую конечный предел, есть величина бесконечно малая.
18. Раскрытие неопределенностей.
Раскрытие неопределенностей – методы вычисления пределов функций, заданных формулами, которые в результате формальной подстановки в них предельных значений аргумента теряют смысл, то есть переходят в выражения типа: бесконечность на бесконечность, ноль на ноль и т.д.
Для раскрытия неопределенностей бесконечность на бесконечность используется следующий алгоритм: выявление старшей степени переменной и деление на эту переменную, как числителя, так и знаменателя.
Для раскрытия неопределенностей ноль на ноль существует следующий алгоритм: разложение на множители числителя и знаменателя и сокращение дроби.
19. Непрерывность функции в точке. Свойства.
Функция непрерывна в точке, если она в этой точке определена, и пределы справа и слева существуют и равны значению в этой точке.
20. Точки разрыва. Их классификация.
Рассматривая некоторую функцию f(x), непрерывную в окрестности точки x0, за исключением может быть самой точки x0. Из определения функции следует, что x=x0 является точкой разрыва, если функция не определена в этой точке, или не является в ней непрерывной. Непрерывность функции может быть односторонней.
Точка x0 называется точкой разрыва 1 рода, если в этой точке функция f(x) имеет конечные, но неравные друг другу левый и правый пределы. Для выполнения условий этого определения не требуется, чтобы функция была определена в точке x=x0, достаточно того, что она определена справа и слева от нее. Из определения можно сделать вывод, что в точке разрыва 1 рода функция может иметь только конечный скачок. В некоторых частных случаях точку разрыва 1 рода еще называют устранимой точкой разрыва.
Точка x0 называется точкой разрыва 2 рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.
21. Свойства функций, непрерывных на отрезке. Формулировка теоремы Коши и ее геометрический смысл.
22. Производная функции, ее геометрический и механический смысл.
Производная функции – основное понятие в дифференциальном исчислении, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Процесс вычисления производной называется дифференцированием.
23. Правила дифференцирования.
24. Дифференциал, определение, геометрический смысл.
Дифференциал – линейная часть приращения функции.
25. Производные и дифференциалы второго порядка. Определения, вычисление.
26. Правило Лопиталя.
Правило Лопиталя – метод нахождения пределов функций, раскрывающий неопределенности вида ноль на ноли или бесконечность на бесконечность. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
27. Применение производных к исследованию функций.
28. Экстремум функции, необходимое и достаточные условия экстремума.
29. Функция нескольких переменных (ФНП). Область определения. Предел и непрерывность ФНП.
30. Частные производные ФНП.
31. Полный дифференциал ФНП.
32. Касательная плоскость и нормаль к поверхности.
33. Производные и дифференциалы высших порядков ФНП.
34. Производная сложной функции (случай нескольких независимых переменных)
35. Производная функций двух переменных, заданной в неявном виде.
36. Экстремум ФНП. Необходимое и достаточное условия экстремума ФНП.
37. Условный экстремум ФНП. Наибольшее и наименьшее значения функции в замкнутой области.
38. Первообразная функции, неопределенный интеграл и его свойства.
Первообразная данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть производная от F равна f. Вычисление первообразной заключается в нахождении неопределенного интеграла, а сам процесс называется интегрированием.
Неопределенный интеграл для функции f(x) – это совокупность всех первообразных данной функции.
Свойства.
Первообразная суммы равна сумме первообразных.
Первообразная произведения константы и функции равна произведения константы и первообразной функции.
Достаточным условием существования первообразной у заданной на отрезке функции f является непрерывность f на этом отрезке.
У заданной на отрезке функции любые две первообразные отличаются на постоянную.
39. Таблица интегралов.
40. Методы вычисления неопределенного интеграла (непосредственное интегрирование, подстановкой, по частям).
Непосредственное интегрирование – метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла сводится к одному или нескольким табличным интегралам.
Метод подстановки. Заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся.
Интегрирование по частям – один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных функций, то справедлива следующая формула: интеграл udv = uv – интеграл vdu
41. Интегрирование рациональных дробей.
Неопределенный интеграл от любой рациональной дроби на всяком промежутке, в котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно является алгебраической суммой суперпозиции рациональных дробей.
42. Интегрирование выражений, содержащих тригонометрические функции.
43. Универсальная тригонометрическая подстановка.
Универсальная тригонометрическая подстановка применяется в интегрировании для нахождения первообразных, определенных и неопределенных интегралов от рациональных функций от тригонометрических функций. Без потерь общности можно считать в данном случае такие функции рациональными функциями от синуса и косинуса. Подстановка использует тангенс половинного угла.
44. Интегрирование рациональностей.
45. Определенный интеграл как предел интегральных сумм.
Определенный интеграл – аддитивный монотонный нормированный функционал, заданный на множестве пар, первая компонента из них есть интегрируемая функция или функционал, а вторая – область во множестве задания этой функции (функционала).
46. Формула Ньютона-Лейбница. Свойства определенного интеграла.
Формула Ньютон-Лейбница или основная теорема анализа дает соотношение между двумя операциями: взятием определенного интеграла и вычислением первообразной. Если f непрерывна на отрезке от a до b, включая их и Ф – ее любая первообразная на этом отрезке, то имеет место равенство: интеграл от a до b f(x)dx = Ф(b) – Ф(a) = Ф от a до b.
Свойства.
Производная от определенного интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела.
Определенный интеграл от суммы функций равен сумме неопределенных интегралов.
Постоянный множитель можно выносить за знак определенного интеграла.
Если поменять местами верхний и нижний пределы интегрирования, то определенный интеграл изменит знак.
47. Методы вычислений определенного интеграла (непосредственное, подстановкой, по частям).
48. Приложения определенного интеграла: Вычисление площади плоской фигуры, объема тела вращения, длины кривой.
49. Несобственные интегралы.
Определенный интеграл называется несобственным, если выполняется, по крайней мере, одно из следующих условий: предел a или b (или оба предела) являются бесконечными, функция f(x) имеет одну или несколько точек разрыва внутри отрезка [a;b]
50. Двойные интегралы, определение, вычисление.
Двойным интеграл называется предел двойной интегральной суммы при условии стремления к нулю диаметров всех ячеек, если он существует и не зависит от способа разбиения области D, от способа выбора точек C внутри каждой ячейки.
Вычисление. Двойной интеграл D f(x;y)dxdy = интеграл dx * интеграл f(x;y)dy
51. Замена переменных в двойном интеграле.
52. Тройные интегралы, определение, вычисление.
Тройным интегралом называют кратный интеграл с d=3
53. Замена переменных в тройном интеграле.
54. Применение кратных интегралов к вычислению площадей, объемов.
55. Криволинейные интегралы 1 и 2 рода. Определение и вычисление.
56. Формула Грина.
Формула Грина устанавливает связь между криволинейным интегралом по замкнутому контуру C и двойным интегралом по односвязной области D, ограниченной эти контуром.
Интеграл по замкнутому контуру C Pdx + Qdy = двойной интеграл D (dQ/dx – dP/dy) dxdy
57. Дифференциальные уравнения 1-го порядка, задачи Коши.
58. Линейные дифференциальные уравнения первого порядка. Решение методом Бернулли и методом вариации произвольных постоянных.
59. Однородные дифференциальные уравнения первого порядка.
60. Дифференциальные уравнения, допускающие понижение порядка.
61. Структура общего решения линейного неоднородного дифференциального уравнения.
62. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами с правой частью специального вида. Метод неопределенных коэффициентов.
63. Скалярное и векторное поля. Поверхности уровня и градиент скалярного поля.
Если каждой точке M заданной области пространства (чаще всего размерности 2 или 3) поставлено в соответствие некоторое число u, то говорят, что в этой области задано скалярное поле. Скалярное поле – это функция, отображающая R в степени n в R.
Векторное поле – это отображение, которое в каждой точке рассматриваемого пространства ставит в соответствии вектор с началом в этой точке
Поверхностью уровня скалярного поля u = u(x;y;z) называется множество точек пространства, в которых функция u принимает одно и то же значение c, то есть поверхность уровня определяется уравнением u(x;y;z) = c.
Градиент grad u – направление скорейшего возрастания поля u = u(r) = u(x;y;z) указывает вектор градиента.
Абсолютная величина вектора градиента u есть производная u по направлению скорейшего роста (скорость роста u при движении с единичной скоростью в этом направлении).
Градиент всегда перпендикулярен поверхностям уровня (в двумерном случае — линиям уровня). Исключение — особые точки поля, в которых градиент равен нулю.
64. Векторное поле, векторные линии. Дивергенция векторного поля.
Если каждой точке M заданной области пространства (чаще всего размерности 2 или 3) поставлено в соответствие некоторое число u, то говорят, что в этой области задано скалярное поле. Скалярное поле – это функция, отображающая R в степени n в R.
Векторные линии (интегральная кривая) для поля F(r) называется кривая r=r(t), касательная к которой во всех точках кривой совпадает со значением поля: dr/dt = F(r(t)).
Дивергенция – дифференциальный оператор, отображающий векторное поле на скалярное (то есть операция дифференцирования, в результате применения которой к векторному полю получается скалярное поле) который определяет (для каждой точки) насколько расходится входящее и исходящее из малой окрестности данной точки поле. Более краткое определение дивергенции: это линейный дифференциальный оператор на векторном поле, характеризующий поток данного поля через поверхность достаточно малой окрестности каждой внутренней точки области определения поля.
65. Циркуляция и ротор векторного поля.
Циркуляцией векторного поля по данному замкнутому контуру Г называется криволинейный интеграл второго рода, взятый по Г. По определению C = интеграл по замкнутому контуру Г Fdl = интеграл по замкнутому контуру Fxdx + Fydy + Fzdz
Ротор или вихрь – векторный дифференциальный оператор над векторным полем.
66. Потенциальные и соленоидальные поля.
Потенциальное (безвихревое) поле – векторное поле, которое можно представить как градиент некоторой скалярной функции координат (потенциала). Необходимым условием потенциальности векторного поля в трехмерном пространстве является равенство нулю ротора поля.
Векторное поле является соленоидальным или вихревым, если через любую замкнутую поверхность S его поток равен нулю.
67. Числовые ряды, основные определения. Сходимость и сумма ряда.
Числовым рядом называется бесконечная последовательность чисел u1, u2…un соединенных знаком сложения.
Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм. Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.
Сумма числового ряда определяется как предел, к которому стремятся суммы первых n слагаемых ряда, когда n неограниченно растет. Если такой предел существует и конечен, то ряд сходится, в противном случае – расходится.
68. Знакоположительные ряды. Достаточные признаки сходимости.
Знакоположительным называется ряд, если все числа, входящие в ряд положительны, неотрицательны.
Признак Даламбера. Признак сравнения. Радикальный признак Коши. Интегральный признак Коши.
69. Знакопеременные ряды. Абсолютная и условная сходимость.
Знакочередующимся рядом называется ряд, если его члены попеременно принимают значения противоположных знаков.
Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов. Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.
70. Признак Лейбница.
Признак Лейбница – теорема об условной сходимости знакочередующихся рядов.
S=Ряд от 1 до бесконечности bi сходится, если выполняются оба условия: 1. Модуль bi+1 меньше модуля bi. 2.Предел при i, стремящимся к бесконечности модуль bi = 0.
71. Степенные ряды. Теорема Абеля.
Степенной ряд – это формальное алгебраическое выражение вида: F(X) = Ряд от 0 до бесконечности an*X в степени n
Теорема Абеля. Признак Абеля дает достаточные условия сходимости числового ряда. Числовой ряд от 0 до бесконечности anbn сходится, если выполнены следующие условия: 1. Последовательность an монотонна и ограничена. 2. Числовой ряд от нуля до бесконечности bn сходится.
72. Ряды Тейлора и Маклорена.
Ряд Тейлора – разложение функции в бесконечную сумму степенных функций. Пусть функция f(x) бесконечно дифференцируема в некоторой окрестности точки a. Формальный ряд: Ряд от 0 до бесконечности, в знаменателе f в степени k умноженная на a / k! * (x-a) в степени k называется рядом Тейлора функции f в точке a. В случае, если a = 0, этот ряд называется рядом Маклорена.
73. Разложение функций в степенные ряды.
Функция, аналитическая в области D, в окрестности каждой точки z0 этой области представляется в виде степенного ряда f(z) = Сумма от 0 до бесконечности cn (z-z0) в степени n, радиус сходимости R, которого не меньше, чем расстояние от точки z0 до границы области D. Алгоритм вычисления: найти производные от данной функции, вычислить значения производных в точке z0, найти область сходимости полученного ряда.
74. Комплексные числа. Алгебраическая, тригонометрическая и показательная формы записи, действия над ними.
Комплексные числа – числа вида x+iy, где x и y – вещественные числа, i – мнимая единица.
Тригонометрическая форма записи ф=ф0+2kп
Показательная форма записи z=re в степени iф
Действия над комплексными числами.
Суммой комплексных чисел z1 и z2 называется комплексное число z=(x1+x2,y1+y2)
Произведением комплексных чисел z1 и z2 называется комплексное число z=(x1x2-y1y2,x1y2-x2y1)
Разностью комплексных чисел z1 и z2 называется комплексное число z такое, что z2+z=z1, откуда z=z1-z2=(x1-x2,y1-y2)
Частным комплексных чисел z1 и z2 называется комплексное число z такое, что z2*z=z1. Отсюда z=(x1x2+y1y2/x2^2+y2^2, x2y1-x1y2/x2^2+y2^2)
75. Комплексная плоскость. Модуль и аргумент комплексного числа. Главное значение аргумента. Геометрический смысл.
Комплексная плоскость – это двумерное вещественное пространство R^2, которое изоморфно полю комплексных чисел C. Каждая точка такого пространства – это упорядоченная пара вида (x,y), где x и y – вещественные числа, и где первый элемент пары соответствует вещественной части, а второй элемент пары соответствует мнимой части комплексного числа z=x+iy x=Re z, y=Im z
76. Функция комплексного переменного.
77. Производная функции комплексного переменного. Условия Коши-Римана.
78. Интегрирование функции комплексного переменного.
79. Интегральная формула Коши.
Пусть D – область на комплексной плоскости с кусочно-гладкой границей Г = дельта D, функция f(z) – голоморфна в D и z0 – точка внутри области D. Тогда справедлива следующая формула Коши: f(z0) = 1/2пi * интеграл Г f(z)/z-z0 dz. Формула справедлива также, если предполагать, что f(z) голоморфна внутри D, и непрерывна на замыкании, а также если граница D не кусочно-гладкая, а всего лишь спрямляемая.
80. Изолированные особые точки, их классификация.
Изолированная особая точка – точка, в некоторой проколотой окрестности которой функция f(z) однозначна и аналитична, а в самой точке либо не задана, либо не дифференцируема.
Классификация.
Устранимая особая точка – называется особой точкой функции f(z), голоморфной в некоторой проколотой окрестности этой точки, если существует конечный предел z стремится к z0 f(z) = B, B принадлежит C.
Полюс – называется голоморфной точкой в некоторой проколотой окрестности этой точки, если существует предел z стремится к z0 f(z) = бесконечность.
Существенно особая точка – называется голоморфной точкой в некоторой проколотой окрестности этой точки, если предел z стремится к z0 f(z) – не существует.
81. Вычеты и формулы для их вычисления.
Пусть 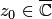 — изолированная особая точка функции
— изолированная особая точка функции 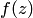 . По определению изолированной особой точки существует некоторая окрестность этой точки, в которой
. По определению изолированной особой точки существует некоторая окрестность этой точки, в которой 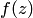 — аналитическая. Напомним, что для
— аналитическая. Напомним, что для  эта окрестность имеет вид
эта окрестность имеет вид 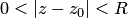 , а для
, а для  —
— 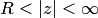
Вычетом функции 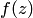 в изолированной особой точке
в изолированной особой точке 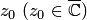 называется интеграл
называется интеграл 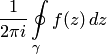 , где
, где 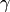 — контур, принадлежащий окрестности точки
— контур, принадлежащий окрестности точки 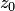 и охватывающий ее.
и охватывающий ее.
Основная теорема о вычетах
Интеграл по замкнутому контуру f(z)dz = 2пi * Сумма от 1 до n res f(z)
Основы вероятностного анализа.
82. Классификация событий. Сумма, произведение событий, их свойства, графическое представление.
Одним из основных понятий теории вероятностей является понятие события. Под событием понимают любой факт, который может произойти в результате опыта или испытания. Под опытом, или испытанием, понимается осуществление определённого комплекса условий.
Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными. Например, подбрасываются две игральные кости. Событие 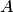 — выпадание трех очков на первой игральной кости, событие
— выпадание трех очков на первой игральной кости, событие 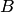 — выпадание трех очков на второй кости.
— выпадание трех очков на второй кости. 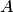 и
и 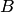 — совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие
— совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие 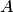 — наудачу взятая коробка окажется с обувью черного цвета, событие
— наудачу взятая коробка окажется с обувью черного цвета, событие 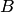 — коробка окажется с обувью коричневого цвета,
— коробка окажется с обувью коричневого цвета, 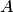 и
и 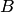 — несовместные события.
— несовместные события.
Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.
Событие называется невозможным, если оно не может произойти в условиях данного опыта. Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная — невозможным.
Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Примером случайного события может служить выявление дефектов изделия при контроле партии готовой продукции, несоответствие размера обрабатываемого изделия заданному, отказ одного из звеньев автоматизированной системы управления.
События называются равновозможными, если по условиям испытания ни одно из этих событий не является объективно более возможным, чем другие
Суммой, или объединением, нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
Сумма 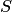 событий
событий 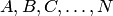 обозначается так:
обозначается так:
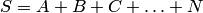 .
.
Произведением, или пересечением, нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Произведение 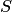 событий
событий 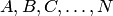 обозначается
обозначается
 .
.
. Свойство 1. Если все случаи являются благоприятствующими данному событию 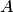 , то это событие обязательно произойдет. Следовательно, рассматриваемое событие является достоверным, а вероятность его появления
, то это событие обязательно произойдет. Следовательно, рассматриваемое событие является достоверным, а вероятность его появления  , так как в этом случае
, так как в этом случае 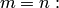
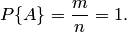
Свойство 2. Если нет ни одного случая, благоприятствующего данному событию 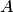 , то это событие в результате опыта произойти не может. Следовательно, рассматриваемое событие является невозможным, а вероятность его появления
, то это событие в результате опыта произойти не может. Следовательно, рассматриваемое событие является невозможным, а вероятность его появления 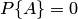 , так как в этом случае
, так как в этом случае 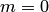 :
:

Свойство 3. Вероятность наступления событий, образующих полную группу, равна единице.
Свойство 4. Вероятность наступления противоположного события 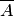 определяется так же, как и вероятность наступления, события
определяется так же, как и вероятность наступления, события 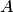 :
:
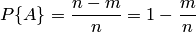
где 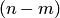 — число случаев, благоприятствующих появлению противоположного события
— число случаев, благоприятствующих появлению противоположного события 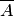 . Отсюда вероятность наступления противоположного события
. Отсюда вероятность наступления противоположного события 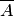 равна разнице между единицей и вероятностью наступления события
равна разнице между единицей и вероятностью наступления события 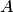 :
:
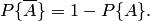
Важное достоинство классического определения вероятности события состоит в том, что с его помощью вероятность события можно определить, не прибегая к опыту, а исходя из логических рассуждений.
83. Различные определения вероятностей.
Классическое определение вероятности случайного события.
Вероятность события 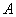 равна отношению числа благоприятных событию
равна отношению числа благоприятных событию 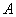 исходов опыта к общему числу исходов опыта.
исходов опыта к общему числу исходов опыта.
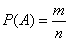 , где
, где
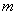 - число благоприятных исходов опыта;
- число благоприятных исходов опыта;
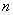 - общее число исходов опыта.
- общее число исходов опыта.
84. Формулы сложения и умножения вероятностей событий.
Теорема. Вероятность суммы конечного числа несовместных событий  равна сумме вероятностей этих событий
равна сумме вероятностей этих событий
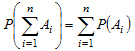
Теорема. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место
P(AB) = P(A)×P(B/A) = P(B)×P(A/B).
Теорема. Вероятность произведения конечного числа событий равна произведению их условных вероятностей относительно произведения предшествующих событий, т.е.
P(ABC....LM) = P(A)×P(B/A)×P(C/AB) P(M/AB...L).
Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления
P(A+B) = P(A) + P(B) — P(AB).
85. Схема Бернулли повторных испытаний. Формула Бернулли.
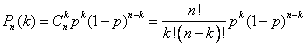 - вероятность появления события ровно
- вероятность появления события ровно 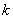 раз при
раз при 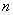 независимых испытаниях,
независимых испытаниях,  - вероятность появления события при одном испытании.
- вероятность появления события при одном испытании.
86. Локальная и интегральная формула Лапласа.
 - вероятность появления события ровно
- вероятность появления события ровно 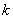 раз при
раз при 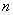 независимых испытаниях,
независимых испытаниях,  - вероятность появления события при одном испытании,
- вероятность появления события при одном испытании, 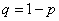
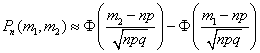 - вероятность появления события не менее m1 и не более m2 раз при
- вероятность появления события не менее m1 и не более m2 раз при 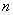 независимых испытаниях,
независимых испытаниях,  - вероятность появления события при одном испытании,
- вероятность появления события при одном испытании, 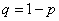 .
.
87. Закон распределения вероятностей дискретной случайной величины. Числовые характеристики.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и вероятностями их появления.
Таблица соответствия значений случайной величины и их вероятностей вида
| x1 | x2 | x3 | ... | xn | ... |
| p1 | p2 | p3 | pn |
Графическое представление этой таблицы называется многоугольником распределения. По оси абсцисс откладываются возможные значения дискретной случайной величины, а по оси ординат соответствующие вероятности.

Числовые характеристики дискретных случайных величин
Закон распределения полностью характеризует дискретную случайную величину. Однако, когда невозможно определить закон распределения, или этого не требуется, можно ограничиться нахождением значений, называемых числовыми характеристиками случайной величины:
- Математическое ожидание,
- Дисперсия,
- Среднее квадратичное отклонение
Эти величины определяют некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения.
Математическое ожидание M дискретной случайной величины - это среднее значение случайной величины, равное сумме произведений всех возможных значений случайной величины на их вероятности.
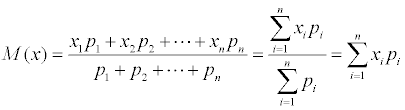
Дисперсия случайной величины — мера разброса случайной величины, равная математическому ожиданию квадрата отклонения случайной величины от ее математического ожидания.
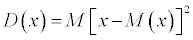
Принимая во внимание свойства математического ожидания, легко показать что
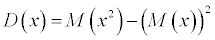
Средним квадратическим отклонением случайной величины (иногда применяется термин «стандартное отклонение случайной величины») называется число равное
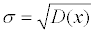
88. Законы распределения: биноминальный, Пуассона, равномерный, показательный, нормальный.
Биномиальный закон (распределение Бернулли)
Производящая функция биномиального распределения задаётся формулой
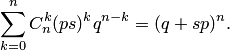
Закон распределения Пуассона (закон редких событий)
Случайная величина 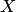 называется распределённой по закону Пуассона с параметром
называется распределённой по закону Пуассона с параметром 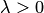 , если
, если
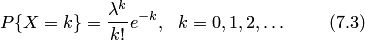
Производящая функции распределения Пуассона задаётся формулой

Равномерное распределение задаётся следующим законом:

Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Случайная величина 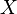 имеет экспоненциальное распределение с параметром
имеет экспоненциальное распределение с параметром  , если её плотность имеет вид
, если её плотность имеет вид
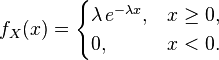 .
.
Нормальное распределение,[1][2] также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задается функцией плотности вероятности, совпадающей с функцией Гаусса:
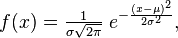
89. Числовые характеристики дискретных и непрерывных случайных величин.
См. вопрос 87.
90. Статистическое распределение выборки. Полигон и гистограмма.
Полигоном частот называют ломаную, отрезки, которой соединяют точки (х1,n1),(х2,n2),...,(хk,nk). Для построения полигона частот на оси абсцисс откладывают варианты х2, а на оси ординат – соответствующие им частоты ni. Точки (хi,ni) соединяют отрезками и получают полигон частот.
Полигоном относительных частот называют ломаную, отрезки, которой соединяют точки (х1,w1),(х2,w2),...,(хk,wk). Для построения полигона относительных частот на оси абсцисс откладывают варианты хi, а на оси ординат соответствующие им частоты wi. Точки (хi,wi) соединяют отрезками и получают полигон относительных частот.
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению ni/h (плотность частоты).
Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni/h. Площадь i-го частичного прямоугольника равна h•ni/h=ni - сумме частот вариант i-го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению wi/h (плотность относительной частоты).
Не нашли, что искали? Воспользуйтесь поиском: