ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Для каких из матриц , , , не существует обратная
+: A +: B
**Даны матрицы 
и 
. Тогда решение матричного уравнения 
имеет вид …
+: 
**Дана матрица 
. Тогда обратная матрица 
равна …
+: 
**Дана матрица 
. Тогда обратная матрица равна …
+: 
**Дана матрица 
, где 
. Тогда обратная матрица 
может быть представлена в виде …
+: 
**Дана система уравнений 
. Для того, чтобы найти значение переменной y при решении этой системы по формулам Крамера, достаточно вычислить только определители…
**Дана система уравнений 
. Для того, чтобы найти значение переменной y при решении этой системы по формулам Крамера, достаточно вычислить только определители…
+: 
и 
**Даны векторы 
и 
; если 
, то вектор 
равен …
+: 
**Даны векторы 
. Тогда линейная комбинация 
этих векторов равна …
+: 
**Даны векторы 
и 
, где 
, 
и 
– ортонормированный базис. Известно, что скалярное произведение этих векторов равно 40, а угол между этими векторами равен 
. Тогда значение 
равно …
+: 191
**Длина стороны квадрата, площадь которого равна площади параллелограмма, построенного на векторах 
и 
, равна …
+: 
**Даны векторы 
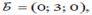
Смешанное произведение 
Тогда значение m равно …
Длина ребра куба, объем которого равен объему параллелепипеда, построенного на векторах 
, равна … +: 2
***Даны графики прямых:
Тогда сумма их угловых коэффициентов равна… +: 3
** *Даны графики прямых 
:
Тогда сумма их угловых коэффициентов равна… +: 2
***Даны графики прямых 
:
Тогда сумма их угловых коэффициентов равна… +: 2
***Даны графики прямых 
:
Тогда сумма их угловых коэффициентов равна… +: 1
***Даны графики прямых 
:
Тогда сумма их угловых коэффициентов равна… +: 0
***Даны графики прямых 
:
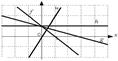
Тогда наименьший угловой коэффициент имеет прямая… +: f
***Даны прямая линия 
и плоскость 
в пространстве. Тогда прямая l …
+: принадлежит плоскости 
1***Если для рядов 
и 
с положительными членами выполняется неравенство 
, то:
+: из сходимости следует сходимость 
+: из расходимости следует расходимость 
2.Если разложение в ряд Маклорена функции 
имеет вид 
, то коэффициент 
разложения функции 
в ряд Маклорена равен …
+: 
3.Если функция 
в окрестности точки 
представлена своим рядом Тейлора, то коэффициент при 
в этом ряде равен …
+: 
4.Если 
, то коэффициент а 5 разложения данной функции в ряд Тейлора по степеням (х –3) равен…
+: 0
5.Если 
, то коэффициент а 6 разложения данной функции в ряд Тейлора по степеням (х +4) равен…
+: 0
6.Если 
, то коэффициент 
разложения данной функции в ряд Тейлора по степеням (х– 1) равен…
+: 0
7.Если 
, то коэффициент 
разложения данной функции в ряд Тейлора по степеням (х– 1) равен…
+: 0
8.Если 
, то коэффициент разложения данной функции в ряд по степеням (х +3) равен...
+: 0
9.Если 
, то коэффициент 
разложения данной функции в ряд по степеням (х+1) равен...
+: 0
Не нашли, что искали? Воспользуйтесь поиском: