
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Логарифмическая функция обратна к показательной
Графики логарифмических функций

Логарифмическая функция обратна к показательной

№17
Числовая функция (в математике) — это функция, которая действует из одного числового пространства (множества) в другое числовое пространство (множество).[1] Числовые множества — это множества натуральных,
8.10.13(1)
№18
Пусть функция  строго монотонная (возрастающая или убывающая) и непрерывная на области определения
строго монотонная (возрастающая или убывающая) и непрерывная на области определения  , область значений этой функции
, область значений этой функции 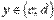 , тогда на интервале
, тогда на интервале  определена непрерывная строго монотонная функция
определена непрерывная строго монотонная функция  с бластью значений
с бластью значений 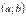 , которая является обратной для
, которая является обратной для  . Другими словами, об обратной функции
. Другими словами, об обратной функции  для функции
для функции  на конкретном промежутке имеет смысл говорить, если на этом интервале
на конкретном промежутке имеет смысл говорить, если на этом интервале  либо возрастает, либо убывает. Функции f и g называют взаимно обратными. Зачем вообще рассматривать понятие обратных функций? Это вызвано задачей решения уравнений
либо возрастает, либо убывает. Функции f и g называют взаимно обратными. Зачем вообще рассматривать понятие обратных функций? Это вызвано задачей решения уравнений  . Решения как раз и записываются через обратные функции. Примеры нахождения взаимнообратных функций.Например, требуется решить уравнение
. Решения как раз и записываются через обратные функции. Примеры нахождения взаимнообратных функций.Например, требуется решить уравнение  .
.
Решениями являются точки 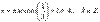 . Функции косинус и арккосинус как раз являются обратными на области определения. Рассмотрим несколько примеров нахождения обратных функций. Начнем с линейных взаимнообратных функций. №19 числовая функция — это функция, которая задана на произвольном (чаще всего) метрическом пространстве и имеет значения в области вещественных чисел
. Функции косинус и арккосинус как раз являются обратными на области определения. Рассмотрим несколько примеров нахождения обратных функций. Начнем с линейных взаимнообратных функций. №19 числовая функция — это функция, которая задана на произвольном (чаще всего) метрическом пространстве и имеет значения в области вещественных чисел
функцией расстояния, заданной на соответствующем
множестве.
В самом общем случае, числовая функция — это
функция, которая задана на произвольном (чаще всего)
метрическом пространстве и имеет значения в области
вещественных чисел
№4 Величина ех, называемая абсолютной погрешностью приближенного значения х, в большинстве случаев остается неизвестной, так как для ее вычисления нужно точное значение X. Вместе с тем, на практике обычно удается установить верхнюю границу абсолютной погрешности, т.е. такое (по возможности наименьшее) число для которого справедливо неравенство Цифра числа называется верной (в широком смысле), если ее абсолютная погрешность не превосходит единицы разряда, в котором стоит эта цифра. Приближенные числа записываются в форме х ± Dх. Запись X = х ± Dx означает, что неизвестная величина X удовлетворяет следующим неравенствам: x-Dx <= X <= x+Dx
№7 Линейные неравентва — это неравентва вида  , либо
, либо  , либо
, либо 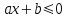 , либо
, либо 
№15 Вернемся к уравнению ах = b, где а>0 и а≠1. Как показано в предыдущем пункте, это уравнение не имеет решений при b≤0 и имеет единственный корень в случае b>0. Этот корень называют логарифмом b по основанию а и обозначают logab, т. е.аlogab = b.
Определение.
Логарифмом числа b по основанию а называется показатель степени, в которую нужно возвести основание а, чтобы получить число b.
Формулу аlogab = b (где b>0, а>0 и а≠1) называют основным логарифмическим тождеством.
№14 Если немного перефразировать - Логарифм числа  по основанию
по основанию  определяется как показатель степени, в которую надо возвести число
определяется как показатель степени, в которую надо возвести число  , чтобы получить число
, чтобы получить число  (Логарифм существует только у положительных чисел).Логарифм в переводе с греческого буквально означает "число, изменяющее отношение". Специальные обозначения:
(Логарифм существует только у положительных чисел).Логарифм в переводе с греческого буквально означает "число, изменяющее отношение". Специальные обозначения:
1. Натуральный логарифм  - логарифм по основанию
- логарифм по основанию  , где
, где  - число Эйлера.
- число Эйлера.
2. Десятичный логарифм  - логарифм по основанию 10.
- логарифм по основанию 10.
Свойства логарифмов: 1°  - основное логарифмическое тождество.2°
- основное логарифмическое тождество.2°  3°
3°  Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень.4°
Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень.4°  - логарифм произведения.Логарифм произведения равен сумме логарифмов сомножителей.
- логарифм произведения.Логарифм произведения равен сумме логарифмов сомножителей.
 - логарифм частного.Логарифм частного (дроби) равен разности логарифмов сомножителей.6°
- логарифм частного.Логарифм частного (дроби) равен разности логарифмов сомножителей.6° 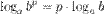 - логарифм степени.Логарифм степени равен произведению показателя степени на логарифм ее основания.7°
- логарифм степени.Логарифм степени равен произведению показателя степени на логарифм ее основания.7°  8°
8°  9°
9° 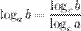 - переход к новому основанию.
- переход к новому основанию.
№20 Соотношение радиана с другими единицами измерения углов описывается формулой:
1 радиан = 1/2π оборотов = 180/π градусов = 200/π градов
Очевидно, 180° = π. Отсюда вытекает тривиальная формула пересчёта из градусов, минут и секунд в радианы и наоборот.
α[рад] = (π / 180) × α[°]
α[°] = (180 / π) × α[рад]
где: α[рад] — угол в радианах, α[°] — угол в градусах
1 рад ≈ 57,295779513° ≈ 57°17′44,806″
№21 
№23 Для любого угла α справедливы равенства:
| sin 2α = 2sinα cosα |
| cos 2α = cos2α – sin2α = 2 cos2α – 1 = 1 – 2sin2α |
| Для любого угла α такого, что α ≠ π/2 + πk, α ≠ π/4 + πn/2 (k, n принадлежат множеству Z), справедливо: tg 2α = 2 tgα/(1 – tg2α) |
| Для любого угла α такого, что α ≠ πk/2 (k принадлежит множеству Z), справедливо: сtg 2α = (ctg2α – 1)/(2ctgα) |
| Формулы для половиннных углов |
| Для любого угла α справедливы равенства: cos2α/2 = (1 + cos α)/2 |
| sin2α/2 = (1 – cos α)/2 |
| Для любого угла α такого, что α ≠ π + 2πk (k принадлежит множеству Z), справедливо: tg2α/2 = (1 – cos α)/(1 + cos α) |
| ctg2α/2 = (1 + cos α)/(1 – cos α) |
| tg α/2 = sin α/(1 + cos α) |
| cos α = (1 – tg2α/2)/(1 + tg2α/2) |
| sin α = (2 tg α/2)/(1 + tg2α/2) |
| Для любого угла α такого, что α ≠ πk (k принадлежит множеству Z), справедливо: tg α/2 = (1 – cos α)/(sin α) |
| ctg α = (1 – tg2α/2)/(2 tg α/2) |
| Для любого угла α такого, что α ≠ π + 2πk и α ≠ π/2 + πn (k, n принадлежат множеству Z), справедливо: tg α = (2 tg α/2)/(1 – tg2α/2) |
№291.  Частные случаи
Частные случаи 
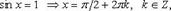
 2.
2.  Частные случаи
Частные случаи 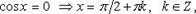

 3.
3. 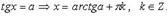 Частные случаи
Частные случаи 

 4.
4. 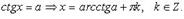 Частные случаи
Частные случаи 

| <== предыдущая лекция | | | следующая лекция ==> |
| Действие нахождение логарифма | | |
Не нашли, что искали? Воспользуйтесь поиском: