
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Вырожденное базисное решение.
Если на каком-либо шаге наибольшее возможное значение переменной достигается в нескольких уравнениях одновременно (совпадают их оценочные отношениянаибольшее возможное значение переменной достигается в нескольких уравнениях одновременно ()ой переменной, которая переводится), то разрешающим является любое из них. На следующем шаге получаем вырожденное базисное решение, переход к очередному базисному решению может не изменить целевую функцию.
Пример 1. Решив (самостоятельно) графическим и симплекс-методом задачи.
Таблица 3.
1. 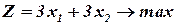
| 2. 
|

| 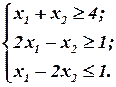
|
получим в задаче №1 отсутствие конечного оптимума 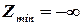 , в задаче №2 альтернативный оптимум
, в задаче №2 альтернативный оптимум  , который достигается во всех точках отрезка
, который достигается во всех точках отрезка 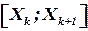 , т.е. в точках
, т.е. в точках  , где
, где  ,
,

Пример 2. Предприятие располагает тремя производственными ресурсами (сырьем, оборудованием, электроэнергией) и может организовать производство продукции двумя различными способами. Расход ресурсов за один месяц и общий ресурс при каждом способе производства даны в таблице (в усл. ед.).
Таблица 4.
| Производственные ресурсы | Расход ресурсов за 1 месяц при работе | Общий ресурс | |
| 1-м способом | 2-м способом | ||
| Сырье | |||
| Оборудование | |||
| Электроэнергия |
При первом способе производства предприятие выпускает за один месяц 3 тыс. изделий, при втором – 4 тыс. изделий.
Сколько месяцев должно работать предприятие каждым из этих способов, чтобы при наличных ресурсах обеспечить максимальный выпуск продукции?
Решение.
Составим математическую модель задачи. Обозначим:  – время работы предприятия первым способом,
– время работы предприятия первым способом, 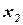 – время работы предприятия вторым способом.
– время работы предприятия вторым способом.
Математическая модель имеет вид  при ограничениях:
при ограничениях: 
Приведем задачу к каноническому виду  при ограничениях:
при ограничениях:

Составляем симплексную таблицу 1-го шага
Таблица А.

| БП | 
| |||||

| 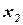
| 
| 
| 
| 
| ||

| 
| ||||||

| |||||||

| |||||||

| -3 | -4 |
Получим решение: 
В индексной строке  имеются две отрицательные оценки, значит, найденное решение не является оптимальным и его можно улучшить. В качестве ключевого столбца следует принять столбец базисной переменной
имеются две отрицательные оценки, значит, найденное решение не является оптимальным и его можно улучшить. В качестве ключевого столбца следует принять столбец базисной переменной 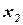 , а за ключевую строку взять строку переменной
, а за ключевую строку взять строку переменной  , где
, где  .
.
Ключевым элементом является 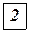 . Вводим столбец базисной переменной
. Вводим столбец базисной переменной 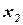 , выводим
, выводим  . Составляем симплексную таблицу 2-го шага. Получим
. Составляем симплексную таблицу 2-го шага. Получим
Таблица Б.

| БП | 
| |||||

| 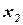
| 
| 
| 
| 
| ||
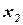
| 1/2 | 1/2 | |||||

| 
| 
| |||||

| 3/2 | 
| |||||

| -1 |
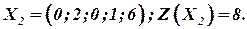
В индексной строке имеется одна отрицательная оценка. Полученное решение можно улучшить. Ключевым элементом является  . Составляем симплексную таблицу 3-го шага.
. Составляем симплексную таблицу 3-го шага.
Таблица В.

| БП | 
| |||||

| 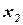
| 
| 
| 
| 
| ||
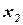
| -1 | ||||||

| -1 | ||||||

| -3 | ||||||

|
Все оценки свободных переменных  , следовательно, найденное опорное решения является оптимальным:
, следовательно, найденное опорное решения является оптимальным: 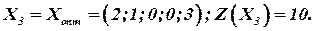
Таким образом, по первому способу предприятие должно работать два месяца, по второму – один месяц, при этом максимальный выпуск продукции составит 10 тыс. ед.
Не нашли, что искали? Воспользуйтесь поиском: