Квантовый эффект Холла

Впервые необычный (англ. unconventional) квантовый эффект Холла наблюдали в работах, где было показано, что носители в графене действительно обладают нулевой эффективной массой, поскольку положения плато на зависимости недиагональной компоненты тензора проводимости соответствовали полуцелым значениям холловской проводимости 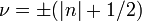в единицах (множитель 4 появляется из-за четырёхкратного вырождения энергии), то есть Это квантование согласуется с теорией квантового эффекта Холла для дираковских безмассовых фермионов. Сравнение целочисленного квантового эффекта Холла в обычной двумерной системе и графене см. на рисунке 6. Здесь показаны уширенные уровни Ландау для электронов (выделение красным цветом) и для дырок (синий цвет). Если уровень Ферми находится между уровнями Ландау, то на зависимости холловской проводимости 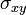наблюдается ряд плато. Эта зависимость отличается от обычных двумерных систем (аналогом может служить двумерный электронный газ в кремнии, который является двухдолинным полупроводником в плоскостях, эквивалентных {100}, то есть тоже обладает четырёхкратным вырождением уровней Ландау, и холловские плато наблюдаются при ).

Квантовый эффект Холла (КЭХ) может использоваться как эталон сопротивления, потому что численное значение наблюдаемого в графене плато, равное 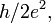воспроизводится с хорошей точностью, хотя качество образцов уступает высокоподвижномуДЭГ в GaAs и, соответственно, точности квантования. Преимущество КЭХ в графене в том, что он наблюдается при комнатной температуре^[53] (в магнитных полях свыше 20 Т). Основное ограничение на наблюдение КЭХ при комнатной температуре накладывает не само размытие распределения Ферми-Дирака, а рассеяние носителей на примесях, что приводит к уширению уровней Ландау.

Рис. 6. a) Квантовый эффект Холла в обычной двумерной системе. b) Квантовый эффект Холла в графене. 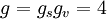— вырождение спектра

В современных образцах графена (лежащих на подложке) вплоть до 45 Т невозможно наблюдать дробный квантовый эффект Холла, но наблюдается целочисленный квантовый эффект Холла, который не совпадает с обычным. В работе^[54] наблюдается спиновое расщепление релятивистских уровней Ландау и снятие четырёхкратного вырождения для наинизшего уровня Ландау вблизи точки электронейтральности. Для объяснения этого эффекта предложено несколько теорий, но недостаточное количество экспериментального материала не позволяет выбрать среди них правильную.

Благодаря отсутствию запрещённой зоны в графене в структурах с верхним затвором можно сформировать непрерывный p-n переход, когда напряжение на верхнем затворе позволяет инвертировать знак носителей, задаваемый обратным затвором в графене, где концентрация носителей никогда не обращается в ноль (кроме точки электронейтральности). В таких структурах тоже можно наблюдать квантовый эффект Холла, но из-за неоднородности знака носителей значения холловских плато отличаются от приведённых выше. Для структуры с одним p-n переходом значения квантования холловской проводимости описываются формулой

где и — факторы заполнения в n- и p-области соответственно (p-область находится под верхним затвором), которые могут принимать значения и т. д. Тогда плато в структурах с одним p-n переходом наблюдаются при значениях 1, 3/2, 2, и т. д.

Для структуры с двумя p-n переходами^[57] соответствующие значения холловской проводимости равны

Интересные факты

Рис. 7. Для получения нанотрубки (n, m) графитовую плоскость надо разрезать по направлениям пунктирных линий и свернуть вдоль направления вектора R

· В статье, опубликованной 10 ноября 2005 года в журнале Nature, Константин Новосёлов и Андрей Гейм утверждают, что электрические заряды в графене ведут себя как релятивистские частицы с нулевой эффективной массой. Эти частицы, известные как безмассовые фермионы Дирака, описываются уравнением Дирака, хотя в эффекте Шубникова-де Гааза (осцилляции магнетосопротивления) наблюдаемые осцилляции соответствуют конечной циклотронной массе.

· Так как закон дисперсии для носителей идентичен закону для безмассовых частиц, графен может выступать в качестве экспериментальной лаборатории для квантовой электродинамики.

· Квантовый эффект Холла в графене может наблюдаться даже при комнатной температуре благодаря большой циклотронной энергии, при которой температурное размытие функции распределения Ферми-Дирака меньше этой энергии (это расстояние между первым и нулевым уровнями Ландау равно 1200 K при магнитном поле 9 Т).

· При сворачивании графена в цилиндр (см. рис. 7) получается одностенная нанотрубка. В зависимости от конкретной схемы сворачивания графитовой плоскости, нанотрубки могут обладать или металлическими, или полупроводниковыми свойствами.

· В графене отсутствует вигнеровская кристаллизация^.

· В графене нарушается приближение Борна-Оппенгеймера (адиабатическое приближение), гласящее, что в силу медленного движения ионных остовов решётки их можно включить в рассмотрение как возмущение, известное как фононы решётки, — основное приближение, на котором строится зонная теория твёрдых тел.

· За новаторские эксперименты с графеном Нобелевская премия 2010 года по физике присуждена Андрею Гейму иКонстантину Новосёлову.

· Термоэлектрический эффект для графена превосходит резистивный омический нагрев, что в перспективе позволит создание на его базе схем, не требующих охлаждения.

· В двойном слое графена электроны ведут себя как жидкий кристалл

Не нашли, что искали? Воспользуйтесь поиском: