
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Конструктивная логика А. А. Маркова. Проблема конструктивного понимания логических связок, в частности отрицания и импликации, требует применения в логике специальных точных формальных языков
Проблема конструктивного понимания логических связок, в частности отрицания и импликации, требует применения в логике специальных точных формальных языков. В основе конструктивной математической логики А. А. Маркова лежит идея ступенчатого построения формальных языков. Сначала вводится формальный язык Яо , в котором предложения выражаются по
определенным правилам в виде формул; в нем имеется определение смысла выражения этого языка, т. е. семантика. Правила вывода позволяют, исходя из верных предложений, всегда получать верные предложения.
В конструктивной математике формулируются теоремы существования, утверждающие, что существует объект, удовлетворяющий таким-то требованиям. Под этим подразумевается, что построение такого объекта потенциально осуществимо, т. е. мы владеем способом его построения. Это конструктивное понимание высказываний о существовании отличается от классического. В конструктивной математике и логике иной является и трактовка дизъюнкции, которая понимается как осуществимость указания ее верного члена. «Осуществимость» означает потенциальную осуществимость конструктивного процесса, дающего в результате один из членов дизъюнкции, который должен быть истинным. Классическое же понимание дизъюнкции не предполагает нахождения ее истинного члена.
Новое понимание логических связок требует новой логики. Мы считаем утверждение А. А. Маркова о неединственности логики верным и весьма глубоким: «В самой идее неединственности логики, разумеется, нет ничего удивительного. В самом деле, с какой стати все наши рассуждения, о чем бы мы ни рассуждали, должны управляться одними и теми же законами? Для этого нет никаких оснований. Удивительным, наоборот, было бы, если бы логика была единственна»39.
В конструктивную математическую логику А. А. Марков вводит понятие «разрешимое высказывание» и связанное с ним понятие «прямое отрицание». В логике А. А. Маркова имеется и другой вид отрицания — усиленное отрицание, относящееся к так называемым полуразрешимым высказываниям.
Кроме материальной и усиленной импликации, при установлении истинности которых приходится заботиться об истинности посылки и заключения, А. А. Марков вводит дедуктивную импликацию, определяемую по другому принципу. Дедуктивная импликация «если А, то В» выражает возможность выведения В из А по фиксированным правилам, каждое из которых в применении к верным формулам даст верные формулы. Всякое высказывание, выводимое из истинного высказывания, будет истинным.
Через дедуктивную импликацию А. А. Марков определяет редукционное отрицание (reductio ad absurdum). Редукционное отрицание высказывания А (сформулированного на данном языке) понимается как дедуктивная импликация «если А, то Л», где через Л обозначен абсурд. Это определение отрицания соответствует обычной практике рассуждений математика: математик отрицает ту посылку, из которой вытекает абсурд. Для установления истинности редукционного отрицания высказывания не требуется вникать в смысл этого высказывания. Высказывание, для которого установлена истинность редукционного отрицания, не может быть истинным.
Эти три различных понимания отрицания не вступают в конфликт друг с другом, они согласованы, что, по мнению А. А. Маркова, даст возможность объединить все эти понимания отрицания.
Показательно такое обстоятельство: А. А. Марков строит свои конструктивные логические системы для обоснования конструктивной математики таким образом, что у него получается не одна законченная система, а целая иерархия систем. Это система языков Я 0, Я 1 Я 2, Я 3, Я 4, Я 5,..., Я N (где N — натуральное число) и объемлющего их языка Я ω после Я ω строится язык Я ω`.
Итак, мы склонны думать, что развивающуюся конструктивную логику и математику невозможно вместить в одно формальное исчисление, для этого нужна система, состоящая из целой иерархии систем, в которой будет иерархия отрицаний.
Проблемами конструктивной логики и теории алгоритмов занимается российский математик Н. М. Нагорный и др.
МОДАЛЬНЫЕ ЛОГИКИ
В классической двузначной логике рассматривались простые и сложные ассерторические суждения, т. е. такие, в которых не установлен характер связи между субъектом и предикатом. Например: «Морская вода — соленая» или «Дождь то начинал хлестать теплыми крупными каплями, то переставал».В модальных суждениях раскрывается характер связи между субъектом и предикатом или между отдельными простыми суждениями в сложном модальном суждении. Например: «Необходимо соблюдать правила уличного движения» или «Если будет дуть попутный ветер, то, возможно, мы приплывем в гавань до наступления темноты».
Модальными являются суждения, которые включают модальные операторы (модальные понятия), т. е. слова «необходимо», «возможно», «невозможно», «случайно», «запрещено», «хорошо» и многие другие (см. гл. Ш, § 6 «Деление суждений по модальности»). Модальные суждения рассматриваются в специальном направлении современной формальной логики — в модальной логике.
Изучение модальных суждений имеет длительную и многогранную историю. Мы отметим лишь некоторые из ее аспектов. Модальности в логику были введены Аристотелем. Термин «возможность», по Аристотелю, имеет различный смысл. Возможным он называет и то, что необходимо, и то, что не необходимо, и то, что возможно. Исходя из понимания модальности «возможность», Аристотель писал о неприменимости закона исключенного третьего к будущим единичным событиям.
Наряду с категорическим силлогизмом Аристотель исследует и модальный силлогизм, у которого одна или обе посылки и заключение являются модальными суждениями. Я. Лукасевич в книге «Аристотелевская силлогистика с точки зрения современной формальной логики» две главы посвящает аристотелевой модальной логике предложений и модальной силлогистике Аристотеля40. Аристотель рассматривает модальную силлогистику по образцу своей ассерторической силлогистики: силлогизмы подразделяются на фигуры и модусы, неправильные модусы отбрасываются с помощью их интерпретации на конкретных терминах.
Согласно Аристотелю, случайность есть то, что не необходимо и не невозможно, т. е. р — случайно означает то же самое, что и р — не необходимо и р — не невозможно, но Лукасевич отмечает, что аристотелевская теория случайных силлогизмов полна серьезных ошибок41. Итог Лукасевича такой: пропозициональная модальная логика Аристотеля имеет огромное значение для философии; в работах Аристотеля можно найти все элементы, необходимые для построения полной системы модальной логики; однако Аристотель исходил из двузначной логики42, в то время как модальная логика не может быть двузначной. К идее многозначной логики Аристотель подошел вплотную, рассуждая о «будущем морском сражении». Следуя Аристотелю, Лукасевич в 1920 г. построил первую многозначную (трехзначную) логику. Так осуществляется связь модальных и многозначных логик.
Значительное внимание разработке модальных категорий уделяли философы в Древней Греции и особенно Диодор Крон, рассматривавший модальности в связи с введенной им временной переменной. В средние века модальным категориям также уделялось большое внимание. В XIX в. категорию вероятности разрабатывали Дж. Буль и П. С. Порецкий.
Возникновение модальной логики как системы датируется 1918 годом, когда американский логик и философ Кларенс Ирвинг Льюис (1888—1964) в работе «A Survey of Symbolic Logic» сформулировал модальное исчисление, названное им впоследствии 53.
В книге «Symbolic logic», написанной им совместно с К. Лэнгфордом в 1932 г., он сформулировал еще пять модальных логических систем, связанных с 53 и между собой. Это системы 51, S2, 54, 55, S6.
Приведем описание модальной системы S I43
I. Исходные символы. 1) р, q, r и т. д. — пропозициональные переменные; 2) ~ р — отрицание р; 3)  — конъюнкция р и q; 4)
— конъюнкция р и q; 4)  — строгая импликация льюисовской системы; 5)
— строгая импликация льюисовской системы; 5)  —
—
модальный оператор возможности (возможно р); 6) p = q — строгая эквивалентность, p = q равносильно 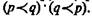
П. Аксиомы системы S 1:
1) 2) 3) 4) 5) 6) 7)
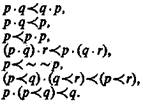
Аксиома 5 может быть выведена из остальных, как было показано позднее. Так как конъюнкция связывает «сильнее», чем импликация, то скобки можно опустить или заменить их точками, как это сделано у Льюиса.
III. Правила вывода S 1.
1. Правило подстановки. Любые два эквивалентных друг другу выражения взаимозаменимы.
2. Любая правильно построенная формула может быть подставлена вместо р, или q, или r и т. д. в любом выражении.
3. Если выводимо р и выводимо q, то выводимо 
4. Если выводимо р и выводимо  то выводимо q.
то выводимо q.
Льюис построил модальную пропозициональную логику S 1 в виде расширения немодального (ассерторического) пропозиционального исчисления (сокращенно АПИ). При этом основные черты 51 и других его исчислений были скопированы с формализованной логической системы Principia Mathematica Рассела и Уайтхеда, сформулированы с помощью понятий, только терминологически отличающихся от понятий, использованных в Principia Mathematica. Кроме Рассела и Уайтхеда идеи классической логики развивали многие современные математические логики, например американский логик и математик С. Клини44. Исчисления Льюиса построены аксиоматически по образцу Principia, по аналогии с Principia Льюис доказывает рад специфических теорем.
В классической двузначной логике логическое следование отождествляется с материальной импликацией, допускаются такие формы вывода: 1)  т. е. истинное суждение следует из любого суждения («истина следует откуда угодно») и 2)
т. е. истинное суждение следует из любого суждения («истина следует откуда угодно») и 2)  т. е. из ложного суждения следует любое суждение («из лжи следует все, что угодно»). Это противоречит нашему содержательному, практическому пониманию логического следования, поэтому данные формулы, а также и некоторые другие, и соответствующие им принципы логического следования называются парадоксами материальной импликации.
т. е. из ложного суждения следует любое суждение («из лжи следует все, что угодно»). Это противоречит нашему содержательному, практическому пониманию логического следования, поэтому данные формулы, а также и некоторые другие, и соответствующие им принципы логического следования называются парадоксами материальной импликации.
Льюис создал свои новые системы с целью избежать этих парадоксов и ввести новую импликацию, названную им «строгой импликацией», такую, чтобы логическое следование представлялось не чисто формально, а по смыслу (содержательно) и новая импликация была бы ближе к союзу естественного языка «если, то». В строгой импликации Льюиса  невозможно утверждать антецедент, т. е. р, и отрицать консеквент, т. е. q 45.
невозможно утверждать антецедент, т. е. р, и отрицать консеквент, т. е. q 45.
В системах Льюиса были устранены парадоксы материальной импликации, т. е. формулы 1) и 2) стали невыводимыми, но появились парадоксы строгой импликации. К ним относятся, например, такие формулы: 3)  4)
4) 
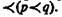 Итак, отождествлять строгую импликацию Льюиса со следованием нельзя.
Итак, отождествлять строгую импликацию Льюиса со следованием нельзя.
С целью исключить парадоксы строгой импликации Льюиса немецкий математик и логик Ф. В. Аккерман (1896—1962) построил свою систему модальной логики. Он ввел так называемую сильную импликацию, которая не тождественна строгой импликации Льюиса, и модальные операторы Аккермана и Льюиса также не являются тождественными. Аккерман все логические термины и модальные операторы определяет через сильную импликацию так: NA равносильно  МА равносильно
МА равносильно  Здесь А — любая правильно построенная формула системы Аккермана: N — оператор необходимости; М — оператор возможности;
Здесь А — любая правильно построенная формула системы Аккермана: N — оператор необходимости; М — оператор возможности;  — отрицание А; знак
— отрицание А; знак  обозначает сильную импликацию. Знак
обозначает сильную импликацию. Знак  — логическая постоянная, обозначающая «абсурдно». Эта постоянная в свою очередь определяется так:
— логическая постоянная, обозначающая «абсурдно». Эта постоянная в свою очередь определяется так: 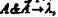 где & обозначает конъюнкцию. И последняя формула читается так: из противоречия, т. е. А и не-А, следует абсурд. В системе Аккермана не выводятся формулы, структурно подобные парадоксам, ни материальной импликации, ни строгой импликации.
где & обозначает конъюнкцию. И последняя формула читается так: из противоречия, т. е. А и не-А, следует абсурд. В системе Аккермана не выводятся формулы, структурно подобные парадоксам, ни материальной импликации, ни строгой импликации.
Системы Льюиса и Аккермана являются бесконечнозначными. В отличие от этих систем первоначально построенные системы Лукасевича являются конечнозначными: одна — трехзначная (1920), другая — четырехзначная (1953). В четырехзначной системе Лукасевича46 также обнаружены парадоксы. Главный из них состоит в том, что ни одно аподиктическое предложение не истинно, т. е. ни одно суждение вида Lot (где L обозначает необходимость, а α — любая формула) не является истинным. Это означало бы, что необходимых суждений нет, т. е. модальный оператор «необходимо» упраздняется. Лукасевич пишет: «Любое аподиктическое предложение должно быть отброшено»47. Сам Лукасевич считает это достоинствοм своей системы, а понятие «необходимость» — псевдопонятием. С такой точкой зрения, конечно, согласиться нельзя.
Интерпретации модальных логик различны. Известный австрийский философ и логик Р. Карнап (1891—1970) пытался интерпретировать модальные понятия (операторы) с помощью так называемой теории «возможных миров», в которой допускается наличие множества «миров», один из которых — действительный, реальный мир, а остальные — возможные миры. Необходимым объявляется то, что существует во всех мирах, возможным — то, что существует хотя бы в одном.
Р. Карнап в 1946 г., используя понятие «описание состояния», предложил интерпретацию модальных операторов, в основе которой лежала идея различия возможного и действительного миров.
В ином направлении шел финский логик Я. Хинтикка. Критически переосмыслив введенное Карнапом понятие «описание состояния», он разрабатывал технику «модальных множеств», т. е. миров (1957), — оригинальную семантическую концепцию возможных миров. Разработка семантики возможных миров для модальных логик продолжается.
Разнообразными проблемами модальной логики занимается американский логик Р. Фейс48.
В настоящее время разработаны многие виды модальностей (см. табл. 7).
Теорией модальных логик и построением новых модальных логических систем в нашей стране активно занимаются логики А. А. Ивин49, Я. А. Слинин50, О. Ф. Серебряников, В. Т. Павлов и др.
Не нашли, что искали? Воспользуйтесь поиском: