Деление окружности на равные части

Многие детали имеют равномерно расположенные по окружности элементы, например отверстия, спицы и т. д. Поэтому возникает необходимость делить окружности на равные части.

Деление окружности на четыре равные части. Чтобы разделить окружность на четыре равные части, нужно провести два взаимно перпендикулярных диаметра.

Два случая таких построений показаны на рисунке 2.34. На рисунке 2.34, а диаметры проведены по линейке и катету равнобедренного угольника, а стороны вписанного квадрата - по его гипотенузе. На рисунке 2.34, б, наоборот, диаметры проведены по гипотенузе угольника, а стороны квадрата — по линейке и катету угольника.

Рис. 2.34. Деление окружности на четыре равные части

Деление окружности на восемь равных частей. Чтобы разделить окружность на восемь равных частей, достаточно провести две пары диаметров, т. е. объединить оба случая построения квадрата.

Одну пару взаимно перпендикулярных диаметров отроят по линейке и катету. другую — но гипотенузе угольника (рис. 2.35).

Рис. 2.35.. Деление окружности на восемь равных частей

Деление окружности на три равные части. Поставив опорную ножку циркуля в конце диаметра (рис. 2.36, а), описывают дугу радиусом, равным радиусу R окружности. Получают первое и второе деление. Третье деление находится на противоположном конце диаметра.

Ту же задачу можно решить с помощью линейки и угольника с углами 30, 60 и 90°. Для этого устанавливают угольник большим катетом параллельно вертикальному диаметру. Вдоль гипотенузы из точки 1 (конца диаметра) проводят хорду, получают второе деление (рис. 2.36, б). Повернув угольник и проведя вторую хорду, получают третье деление (рис. 3, в).

Рис. 2.36. Деление окружности на три равные части: а — с помощью циркуля; б, в— с помощью угольника и линейки

Соединив точки 2 и 3 отрезком прямой, получают равносторонний треугольник.

Деление окружности на шесть равных частей. Раствор циркуля устанавливают равным радиусу R окружности, так как сторона шестиугольника равна радиусу описанной окружности. Из противоположных концов одного из диаметров окружности (например, точек 1 и 4, рис. 2.37, а) описывают дуги. Точки 1, 2, 3. 4, 5, 6 делят окружность на равные части. Соединив их отрезками прямых, получают правильный шестиугольник (рис. 2.37, б).

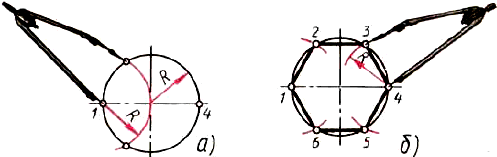
Рис. 2.37. Деление окружности на шесть равных частей с помощью циркуля

Ту же задачу можно выполнить при помощи линейки и угольника с углами 30 и 60° (рис. 2.39).

Рис. 2.39. Деление окружности на шесть равных частей с помощью угольника и линейки

Деление окружности на пять равных частей. Пятой части окружности соответствует центральный угол в 72° (360°:5 = 72°). Этот угол можно построить при помощи транспортира (рис. 2.40, а).

Рис. 2.40. Деление окружности на пять равных частей

На рисунке 2.40, 6 показано вычерчивание пятиконечной звезды.

Постройте с помощью линейки и угольника правильный шестиугольник, две вершины которого лежат на горизонтальной центровой линии. Выполните то же построение с помощью циркуля.

2. Сопряжения.

Плавный переход одной линии в другую называют сопряжением.

Для построения любого сопряжения надо найти центр сопряжения, точки сопряжений, знать радиус сопряжения.

При построении сопряжений следует иметь в виду, что переход от прямой к окружности будет плавным в том случае, если прямая касается окружности (рис. 2.41, а). Точка сопряжения лежит на радиусе, перпендикулярном данной прямой.

Рис. 2.41. Построение сопряжений

Переход от одной окружности к другой будет плавным, если окружности касаются. Точка сопряжения находится на прямой, соединяющей их центры (рис. 2.41. б).

Не нашли, что искали? Воспользуйтесь поиском: