
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
К выбору типа регулятора
Таблица 1.2
Элементы структурных схем
| Звено с одним выходом | Звено с двумя входами | Узел (разветвление) | Сумматор | Элемент сравнения | ||||||||||||||
  

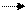  X W Y
Y = W X X W Y
Y = W X
|  X2 X2
 W2
X1 Y
W2
X1 Y
  W1
Y = W1 X1 +
W2 X2 W1
Y = W1 X1 +
W2 X2
|
X X
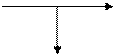 X
X
|
X2 X1
Y = X1 + X2
|
X1 Y
-X2
Y = X1 - X2
|
1.2.2.Правила преобразования структурных схем.
Рассмотрим вначале простейшие сочетания звеньев.
Последовательное соединение звеньев. Последовательным называют такое соединение звеньев, у которого каждая входная величина последующего звена является выходной предыдущего (рис.1.2). В этом случае нетрудно показать, что результирующая передаточная функция равна произведению передаточных функций отдельных звеньев.



 X Yрез
X Yрез





 W1 W2... Wn-1 Wn
W1 W2... Wn-1 Wn
Рис.1.2
Wрез = W1 W2... Wn-1 Wn (1.1)
Параллельное соединение звеньев. Параллельным называют такое соединение звеньев, у которых имеется общая входная величина, а выходная - представляет собой сумму выходных величин всех звеньев, входящих в соединение (рис.1.3). В этом случае результирующая передаточная функция равна сумме передаточных функций звеньев.



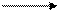 W1
W1
 Y1
Y1
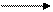

 X W2 Y2
X W2 Y2
..
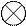 ..
..


 ..
..


 Wn-1 Y
Wn-1 Y
Yn-1

 Wn Yn
Wn Yn
Рис.1.3
Wрез = W1 + W2 +... + Wn-1 + Wn (1.2)
Соединения с обратной связью. В этих соединениях два звена соединены так, что выходная величина одного звена подается обратно на его вход через другое звено(в частном случае это звено может быть звеном с единичной передаточной функцией, т.е. формально отсутствовать). Такое соединение звеньев изображено на рис. 1.4. Звено с передаточной функцией W1 называют звеном прямого канала, а звено с передаточной функцией W2 -звеном цепи обратной связи. В зависимости от знака выходной величины звена обратной связи, соединение может быть как с отрицательной (рис.1.4,а), так и с положительной (рис.1.4,б) обратной связью.



 X e=X-Yoc W1 Y e=X+Yoc W1 Y
X e=X-Yoc W1 Y e=X+Yoc W1 Y
 |  |  |  |  |  | ||||||||||
 |  |
-Yoc Yoc





 W2 W2
W2 W2
а) б)
Рис.1.4
Определим в качестве примера результирующую передаточную функцию для такого сочетания звеньев.
В случае отрицательной обратной связи можно записать
Y = W1e = W1X – W1Yoc, (1.3)
в свою очередь,
YOC=W2Y. (1.4)
Подставляя (1.4) в (1.3), получим
W1
 Y = X (1.5)
Y = X (1.5)
1 + W1W2
Из (1.5) следует
W1
 Wрез = (1.6)
Wрез = (1.6)
1 + W1W2
Аналогично определяется передаточная функция для соединений звеньев с положительной обратной связью
W1
 Wрез = (1.7)
Wрез = (1.7)
1 – W1W2
С помощью соотношений (1.1), (1.2), (1.6), (1.7), данных табл. 1.2 и та6л.1.3, определяющих эквивалентные замены типовых соединений звеньев, можно привести структурные схемы линейных замкнутых цепей САУ к одной принципиальной схеме, показанной на рис. 1.5 а. На этой схеме W01 передаточная функция объекта управления по управляющему воздействию и W02 -передаточная функция объекта управления по возмущающему воздействию, Wр - передаточная функция регулятора, У – управляемая величина, f - возмущающее воздействие, Х - задающее (командное) воздействие, ε=Х–У - ошибка регулирования (рассогласование между командным воздействием и управляемой величиной), U - управляющее (регулирующее) воздействие.
В этой структурной схеме элемент сравнения условно вынесен из регулятора. Поскольку регулятор в замкнутых САУ всегда включен в отрицательную обратную связь, то на этот факт в обобщенной структурной схеме указывает отрицательный сектор сумматора против входа регулируемой величины У в элемент сравнения. По каждому из входных сигналов (Х, f, ε) динамика системы может характеризоваться различными передаточными функциями: Wx (передаточная функция САУ относительно регулируемой величины по отношению к задающему воздействию); Wf (передаточная функция САУ относительно регулируемой величины по отношению к возмущающему воздействию); Wε (передаточная функция САУ сигнала ошибки по отношению к командному воздействию)
 |
f

 X3 e U W02 Y
X3 e U W02 Y





 Wр W01
Wр W01
 - Y
- Y
 |
a)
 |
f

 X3 e U W02 Y
X3 e U W02 Y




 Wр W01
Wр W01
 |
~
б)
Рис.1.5.
Найдем соотношения, определяющие каждую из этих передаточных функций, через передаточные функции объекта и регулятора. Соотношение для передаточной функции Wx следует из выражения (1.6).
Wp W01
 Wx = (1.8)
Wx = (1.8)
1 + Wp W01
Для определения передаточной функции выходной величины САР по отношению к возмущающему воздействию f положим X3 = 0.
Тогда
W02
 Wx = (1.9)
Wx = (1.9)
1 + Wp W01
Передаточная функция ошибки рассогласования выходной величины САУ с командным сигналом по отношению к командному воздействию будет иметь вид
 Wε = (1.10)
Wε = (1.10)
1 + Wp W01
Полученные выражения для характерных передаточных функций замкнутых САУ можно обобщить в одно
Wxy
 Wзам =, (1.11)
Wзам =, (1.11)
1 + Wpаз
где Wзам - передаточная функция замкнутой цепи САУ от любого входного до любого выходного сигнала; Wxy -передаточная функция участка цепи от места приложения воздействия Х до любой величины Y; Wpаз - передаточная функция разомкнутой САУ.
Действительно, анализируя выражения (1.9), (1.10), (1.11), легко убедиться, что в числителе всегда стоит передаточная функция участка цепи от входного воздействия до рассматриваемой координаты. В знаменателе всюду стоит сумма 1 + Wpаз, в которой второе слагаемое соответствует передаточной функции последовательного соединения объекта с регулятором. Она получается при размыкании САУ по линии обратной связи (рис.1.5 б). После операции размыкания соединение объекта с регулятором становится последовательным, для которого выполняется равенство Wpаз= WpW01. Итак, обобщенное правило для составления передаточной функции замкнутой системы автоматического регулирования формулируется следующим образом: для нахождения передаточной функции замкнутой САУ необходимо в ее числителе записать передаточную функцию соединения звеньев от места приложения воздействия до рассматриваемой координаты, а в знаменателе – { 1 + передаточная функция соответствующей САУ разомкнутой цепи}.
Следует отметить, что иногда составление структурной схемы сопряжено с большими трудностями и может быть сделано только с помощью детального анализа дифференциальных уравнений САУ. В этом случае структурная схема не облегчает нахождение основных уравнений системы, но является весьма ценной, так как на ней в наглядной форме представлены все узлы исследуемой системы и все существующие между ними связи. Это может оказаться полезным во всех дальнейших исследованиях.
Правила преобразования структурных схем
Таблица 1.3

2. ЗАДАЧА №2: Построение динамических моделей типовых регуляторов оборотов ГТД.
2.1. Цель, порядок выполнения и выбор варианта задания
Целью выполнения данного задания является приобретение навыков моделирования и анализа систем автоматического управления.
Процесс выполнения задания должен включать в себя следующие этапы.
1.Изобразить исходную (соответствующему Вашему варианту) типовую принципиальную схему САР оборотов ГТД. Схема выбирается из вариантов, приведенных на рис.2.1 по последней цифре номера зачетной книжки с использованием табл.2.1.
2. Изобразить функциональную схему, которая соответствует выбранной в предыдущем пункте типовой САР.
3. Для каждого элемента функциональной схемы запишите уравнение динамики и передаточной функции. В уравнениях динамики переменные должны соответствовать входным и выходным величинам, показанным на структурной схеме. Уравнения динамики типовых элементов (звеньев) сведены в табл.2.2.
4. Изобразите структурную схему. Используя правила преобразования структурных схем, найдите передаточные функции замкнутой и разомкнутой систем регулирования.
5. Запишите уравнения динамики замкнутой и разомкнутой САР в форме обыкновенных линейных дифференциальных уравнений.
6. Найдите по табл.2.3, 2.4 численные значения постоянных коэффициентов (времени и усиления), подставьте их в уравнения динамики САР и оцените устойчивость. Устойчивость целесообразно оценивать по алгебраическим критериям (см. теоретические сведения к задаче №3).
2.2.Теоретические сведения к задаче №2.
2.2.1.Принципиальные схемы простейших систем автоматического регулирования оборотов двигателя
Для ТРД в качестве регулируемой координаты часто выбирают обороты n ротора. При отклонении оборотов от заданного значения чувствительный элемент перемещением регулирующего органа изменяет подачу топлива так, чтобы заданная частота вращения восстановилась. При большом разнообразии пневмогидравлических систем ГТД и вариантов конструктивных схем регуляторов целесообразно рассмотреть замкнутые цепи САР с регуляторами, выполненными по типовым принципиальным схемам.

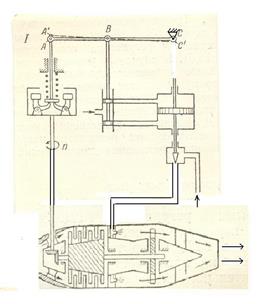
а) б)


в) г)
Рис.2.1 Принципиальные схемы регуляторов оборотов двигателя: а) - статический регулятор прямого действия; б) - астатический регулятор непрямого действия; в) - статический регулятор непрямого действия с жесткой обратной связью; г) - изодромный регулятор
. Таблица 2.1.
К выбору типа регулятора
| № п/п | Последняя цифра шифра | Тип регулятора |
| 1. | 0, 1 | Статический прямого действия |
| 2. | 2, 3 | Астатический непрямого действия без обратной связи |
| 3. | 4, 5, 6 | Непрямого действия с жесткой обратной связью |
| 4. | 7, 8, 9 | Изодромный регулятор |
Таблица 2.2.
Уравнения типовых звеньев
| № | Название звеньев | Уравнения динамики |
| 1. | Чувствительный элемент (ЧЭ) | 
|
| 2. | Преобразующий элемент (ПЭ) | 
|
| 3. | Гидравлический усилитель без обратной связи (УЭ) | 
|
| 4. | Корректирующее звено (КЗ): -жесткая обратная связь (ЖОС) -гибкая обратная связь (ГОС) | 
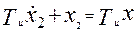
|
| 5. | Регулирующий орган (РО) | 
|
| 6. | Объект регулирования (ОР) | 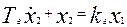
|
Таблица 2.3.
Численные значения коэффициентов уравнений
| Предпоследняя цифра шифра | 
| 
| 
| 
| 
|
| 0,2 | 0,7 | 1,5 | 1,5 | ||
| 0,6 | 1,2 | 0,9 | 1,5 | ||
| 0,7 | 1,0 | 0,4 | 1,5 | ||
| 0,8 | 1,3 | 0,8 | 1,5 | ||
| 0,8 | 1,6 | 1,3 | 1,5 | ||
| 0,3 | 1,1 | 0,7 | 1,5 | ||
| 0,5 | 0,9 | 0,5 | 1,5 | ||
| 0,8 | 1,5 | 1,2 | 1,5 | ||
| 0,4 | 1,4 | 1,1 | 1,5 | ||
| 0,1 | 0,8 | 0,6 | 1,5 |
Таблица 2.4.
Численные значения коэффициентов уравнений
| Последняя цифра шифра | 
| 
| 
| 
| 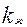
| 
|
| 1,2 | 0,3 | 7,5 | 0,9 | 0,3 | 1,0 | |
| 1,3 | 0,8 | 5,2 | 0,6 | 0,8 | 1,2 | |
| 0,5 | 0,5 | 2,5 | 0,8 | 0,5 | 1,3 | |
| 0,8 | 0,7 | 4,5 | 1,1 | 0,7 | 1,5 | |
| 1,4 | 0,5 | 4,1 | 0,9 | 0,5 | 1,4 | |
| 0,8 | 0,8 | 7,0 | 0,7 | 0,8 | 1,1 | |
| 0,7 | 0,2 | 6,0 | 1,0 | 0,2 | 1,4 | |
| 1,1 | 0,6 | 3,8 | 0,8 | 0,6 | 1,2 | |
| 1,2 | 0,4 | 6,3 | 0,7 | 0,4 | 1,3 | |
| 0,9 | 0,9 | 3,3 | 1,0 | 0,9 | 1,1 |
Это объясняется тем, что любые конструктивные схемы регуляторов классифицируются как несодержащие в своём составе усилителя (регуляторы прямого действия), так и содержащие усилитель (регуляторы непрямого действия). В свою очередь, регуляторы, содержащие усилитель, классифицируют по типу применяемого усилителя, динамические свойства которого являются определяющими свойствами регулятора и системы регулирования в целом. Из рассмотренных ниже усилительных элементов отличительными типовыми свойствами в динамике обладают следующие усилители: интегрирующие, инерционные и изодромные усилители. На рис.2.1 приведены САР оборотов одного и того же объекта регулирования (газогенератора) с четырьмя типовыми регуляторами: прямого действия, с интегрирующим, инерционным и изодромным усилителями.
Регулятором прямого действия называется регулятор, у которого чувствительный элемент непосредственно связан с регулирующим органом. Перемещение регулирующего органа происходит за счет энергии самого чувствительного элемента. На рис.2.1 а) дана одна из возможных схем регулятора частоты вращения прямого действия. Из схемы видно, что чувствительный элемент регулятора состоит из шарнирно закрепленных грузиков 1, муфты и пружины 2. При вращении грузиков развивается центробежная сила, осевая составляющая которой перемещает муфту 2 и связанную с ней через рычаг дозирующую топливную иглу 3 (регулирующий орган). Для настройки регулятора на другую частоту вращения перемещается упор пружины. Такие регуляторы просты и в этом их преимущество. Однако они обладают недостатком с точки зрения требований, предъявляемым к регуляторам ГТД. Этот недостаток связан с тем, что для перемещения регулирующего органа, изменяющего подачу топлива в ГТД, требуются большие усилия. Чтобы их преодолеть потребовалось бы выполнить грузики большой массы, что привело бы к недопустимому увеличению массы и ухудшению динамических свойств системы. Нетрудно убедится, что регулятор, выполненный по этой схеме, дает статическую ошибку регулирования. Поэтому регулятор, показанный на рис.2.1 а), будучи регулятором прямого действия, вместе с тем относится к так называемым статическим регуляторам.
Астатический регулятор непрямого действия изображен на Рис.2.1 б). Регулятором непрямого действия называется регулятор, у которого связь между чувствительным элементом и исполнительным органом осуществляется через промежуточный элемент. Чувствительный элемент регулятора связан с золотником поршневого серводвигателя. Поршень сервомотора с чувствительным элементом жестко не связан, и при данном положении муфты чувствительного элемента может занимать любое положение. Это означает, что регулятор, выполненный по этой схеме, способен поддерживать заданную частоту вращения при различных нагрузках на двигатель. Поэтому он называется астатическим. Однако отсутствие непосредственной связи между чувствительным элементом и дозирующей иглой затрудняет регулирование. Процесс регулирования носит медленно затухающий колебательный характер.
Схема статического регулятора непрямого действия (регуляторы с жесткой обратной связью) показана на Рис.2.1 в). Он (регулятор) является развитием схемы астатического регулятора непрямого действия. В этой схеме движение поршня серводвигателя не остается бесконтрольным. Шток поршня перемещает рычаг АС и золотник, связанный с рычагом АС, уменьшает сечение подвода рабочей жидкости к серводвигателю, приближаясь к нейтральному положению, процесс регулирования быстро заканчивается. В то же время улучшение динамических характеристик рассматриваемого регулятора достигается ценой наличия статической ошибки регулирования.
Изодромный регулятор (Рис.2.1 г) включает в себя достоинства статического регулятора и регулятора с жесткой обратной связью, а именно отсутствие статической ошибки регулирования, хороших динамических характеристик при удачно выбранных параметрах регулятора. Из схемы следует, что в изодромных регуляторах жесткой обратной связи между поршнем серводвигателя и золотником нет. Поршень серводвигателя соединен с рычагом АС не непосредственно, а через специальное устройство, носящее название катаракт. В данной схеме катаракт состоит из поршня 1, связанного с рычагом АС цилиндра 2, пружины 4, которая работает как на сжатие, так и на растяжение. Цилиндр катаракта заполняется вязкой жидкостью. Полости по обе стороны поршня 1 соединены между собой каналом, в который помещен жиклер 3.
Шток поршня катаракта, связанный в точке С с соединительным рычагом АВС, подвешен к неподвижной опоре на пружине 4, которая может работать на растяжение и на сжатие.
Такой сервомотор называется сервомотором с гибкой обратной связью.
2.2.2. Общие принципы и пример решения задачи.
В укрупненном виде система автоматического регулирования оборотами ГТД можно представить в виде функциональной схемы, которая приведена на рис.2.2.


 n0 e Регулятор ГТД n
n0 e Регулятор ГТД n






 (Р) (ОР)
(Р) (ОР)


Рис.2.2. Укрупненная функциональная схема САР.
Схема приведена в предположении, что внешние возмущающие воздействия равны нулю, что соответствует условиям рассматриваемой задачи. На рис.2.2.: n - текущие обороты двигателя (регулируемая величина У); n0 - потребное значение оборотов двигателя (задающее воздействие U); e = n0 – n- отклонение текущих оборотов двигателя от потребных.
В процессе работы автоматической системы величины n и e изменяются во времени. Динамику процесса функционирования САУ в целом можно математически описать некоторым уравнением, связывающим величины n, e и n0). Уравнения динамики записываются так же как и в предыдущей задаче. Дополнительные сведения можно найти в [1, 2].Здесь же ограничимся соображениями общего характера.
Во-первых, принципиальные схемы приведенные на (Рис.2.1) дают лишь представление о принципе работы САУ. Поэтому первым шагом в анализе и моделировании систем управления является детализация функциональной схемы: разбивка САУ на отдельные элементы (звенья) и установление связей между ними. Чтобы унифицировать разбивку систем регулирования на отдельные звенья в теории автоматического управления вводится понятие типового звена. Под типовым звеном понимается такое звено, которое описывается дифференциальным уравнением не выше второго порядка.
Для конкретизации проделаем эту процедуру для системы регулирования оборотами двигателя (Рис.2.1 а).
Вообще говоря, декомпозиция рассматриваемой САУ может быть произвольной, однако имеет смысл провести разбиение на типовые звенья: центробежный измеритель оборотов (чувствительный элемент (ЧЭ)), рычаг АВ (преобразующий элемент (ПЭ)), дозирующую топливную иглу (РО) и собственно сам объект регулирования -двигатель (ОР). Изобразим теперь САУ в виде последовательности из четырех элементов. Соответствующая функциональная схема изображена на рис.3.1.
Вторым шагом при анализе САУ является построение математической модели каждого звена, входящего в структурную схему. Математическое моделирование звена сводится к составлению уравнения, связывающего входную величину с выходной. Входные и выходные величины могут иметь любую физическую природу (напряжение, перемещение, температура, расход топлива, давление и т.д.). Совокупность уравнений и характеристик всех звеньев, описывает динамику процессов управления или регулирования во всей системе.
На третьем шаге по уравнениям динамики каждого звена находятся передаточные функции и составляется структурная схема (рис.3.2.).
На заключительном этапе, в полном соответствии с принципами решения задачи №1, записываются уравнения динамики для САУ в целом.
3. ЗАДАЧА № 3: ОЦЕНКА УСТОЙЧИВОСТИ РАЗОМКНУТЫХ И ЗАМКНУТЫХ САУ
3.1. Цель, исходные данные и последовательность решения задачи
Целью выполнения настоящего задания является получение практических навыков по оценке устойчивости САУ с использованием алгебраических и частотных критериев.
Последовательность решения задачи должнавключать в себя следующие пункты.
1. Используя функциональную схему (рис.3.1.) и структурную схему (рис.3.2.) записать уравнение динамики разомкнутой и замкнутой систем автоматического регулирования в общем виде.
2. По таблицам 3.1….3.3 выбрать значения постоянных времени T22,T1, Tор и коэффициентов усиления k1, k2, k3 , k4 входящих в соотношения для передаточных функций (рис.3.2), соответствующих шифру вашей зачетной книжки, и записать уравнение динамики в виде линейного дифференциального уравнения с известными коэффициентами.
3. Оценить устойчивость разомкнутой системы с помощью алгебраических критериев Рауса и Гурвица.
4. Оценить устойчивость разомкнутой системы с помощью частотного критерия Михайлова.
5. Оценить устойчивость замкнутой системы с помощью частотного критерия Найквиста.
3.2.Выбор варианта задачи и рекомендации по расчетам и оформлению.
Как следует из предыдущего пункта, исходными данными для расчетов являются функциональная и структурная схемы (рис.3.1., рис.3.2), которые для всех вариантов являются общими, и значения коэффициентов T22,T1, Tор,k1, k2, k3,, k4 , которые являются индивидуальными для каждого студента и выбираются в соответствии с номером зачетной книжки по последним трем цифрам.
Коэффициенты T22,T1,k1 уравнения динамики чувствительного элемента (ЧЭ) выбираются по последней цифре номера зачетной книжки в соответствии с табл.3.1.
Коэффициенты усиления k1,k2 преобразующего элемента (ПЭ) и регулирующего органа (РО) выбираются по предпоследней цифре номера зачетной книжки в соответствии с табл.3.2.
Коэффициенты уравнения динамики газотурбинного двигателя (объекта регулирования (ОР)) Tор,k4 выбираются по третьей с конца цифре номера зачетной книжки в соответствии с табл.3.3.
n0 e z1 z2 



 Gт n
Gт n






 ЧЭ ПЭ Р0 ОР
ЧЭ ПЭ Р0 ОР
 |
Рис.3.1. Функциональная схема регулятора оборотов двигателя ГТД



 n0 e z1 z2
n0 e z1 z2




 k1 k2
k1 k2

 Т22p+ Т1p +1
Т22p+ Т1p +1
 |






 k3 Gт k4 n
k3 Gт k4 n
Торp +1
 Рис.3.2. Структурная схема регулятора оборотов ГТД
Рис.3.2. Структурная схема регулятора оборотов ГТД
Построение математической модели САУ, структурная схема которой изображена на рис.3.2, осуществляется также как и в задачах №1 и №2. Сначала записываются результирующие передаточные функции замкнутой и разомкнутой систем регулирования, используя правила преобразования структурных схем, затем записываются соответствующие дифференциальные уравнения, моделирующие функционирование САУ.
Поскольку критерии Михайлова и Найквиста расчетно-графические, то графики должны быть выполнены с четким указанием системы координат и масштабов на отдельных листах. При этом необходимо вычислить и указать на графиках точки пересечения соответствующих кривых с осями координат. В процессе выполнения пунктов 3…5 задания необходимо привести формулировки соответствующих критериев в общем случае и конкретно для вашего уравнения динамики, а затем подставлять конкретные числовые значения
При использовании критерия Найквиста особое значение имеет положение точки с координатами (-1,0) относительно графика Найквиста. Поэтому, в работе необходимо особо выделить процедуру нахождения точки пересечения графика функции Найквиста с осью абсцисс.
Результаты вычислений дискретных значений функций Михайлова и Найквиста, которые необходимы для построения соответствующих графиков, должны быть сведены в таблицы. Интервал дискретизации аргумента функций выбирается таким образом, чтобы в каждом квадранте системы координат находилось не менее трех точек.
Таблица 3.1
| Последняя цифра | Т22 | Т1 | k1 |
| 1,15 | 0,97 | 0,71 | |
| 1,27 | 0,92 | 0,61 | |
| 1,39 | 0,82 | 0,52 | |
| 1,44 | 0,72 | 0,82 | |
| 1,51 | 0,60 | 0,37 | |
| 1,56 | 0,51 | 0,98 | |
| 0,71 | 0,42 | 0,69 | |
| 1,80 | 0,35 | 1,2 | |
| 1,83 | 0,22 | 0,95 | |
| 1,95 | 0,11 | 0,71 |
Таблица 3.2 Таблица 3.3
| Пред- послед-няя цифра | K2 | K3 | Цифра, третья от конца | Тор | k4 | |
| 1,2 | 0,8 | 0,12 | 1,00 | |||
| 0,5 | 1,5 | 0,45 | 0,90 | |||
| 0,9 | 1,1 | 0,13 | 1,12 | |||
| 0,7 | 1,0 | 0,37 | 1,00 | |||
| 1,00 | 0,8 | 0,18 | 0,87 | |||
| 1,25 | 0,97 | 0,25 | 1,15 | |||
| 1,3 | 0,67 | 0,19 | 1,05 | |||
| 1,4 | 0,98 | 0,20 | 0,98 | |||
| 1,5 | 0,7 | 0,22 | 0,95 | |||
| 0,4 | 0,30 |
3.3. Краткие теоретические сведения к задаче №3.
3.3.1. Понятие об устойчивости
Понятие устойчивости системы регулирования связано со способностью возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Устойчивость - это свойство системы возвращаться в исходное установившееся состояние после прекращения воздействия на вход системы или переходить в новое установившееся состояние при сохранении воздействия на вход системы. Система будет устойчивой и в случае, если при внешнем возмущающем воздействии на ее вход новое установившееся состояние не отличается от исходного состояния. Например, устойчивая САУ оборотов ГТД при перемещении РУД должна в короткий период времени перенастроиться и вновь обеспечить постоянство оборотов с заданной погрешностью. Если РУД своего положения не меняет, а меняются внешние воздействия на ГТД (например, давление и температура на входе в двигатель), то устойчивая система должна обеспечить стабилизацию оборотов. Очевидно, что если система неустойчивая, то она и неработоспособна. Поэтому анализ САР всегда начинается с проверки ее устойчивости.
Понятие устойчивости имеет четкий математический смысл и связано с анализом уравнений динамики систем автоматического регулирования. В общем случае, чтобы определить устойчива САУ или нет, необходимо решить уравнение динамики. Этот путь трудоемок и не всегда реализуем даже для линейных систем автоматического регулирования. Поэтому желательно иметь такие критерии, с помощью которых можно было бы судить об устойчивости системы без вычисления корней дифференциальных уравнений динамики. Такие критерии существуют и называются критериями устойчивости.
Все известные критерии можно разбить на две группы: алгебраические, к которым относятся критерии Рауса и Гурвица и частотные - критерии Михайлова и Найквиста.
3.3.2. Алгебраические критерии Рауса и Гурвица
Критерий устойчивости в алгебраической форме был впервые сформулирован Раусом в 1873 году для уравнений четвертой и пятой степеней и 1877 году - полностью. Критерий Рауса формулируется в виде соотношений между коэффициентами левой части уравнений динамики. Т.е. для применения данного критерия нет необходимости решать дифференциальное уравнение, определять корни характеристического уравнения, а нужно лишь знать коэффициенты левой части линейного дифференциального уравнения, моделирующего динамику САР. Алгебраический критерий Рауса для линейных уравнений динамики САР до пятой степени включительно формулируется следующим образом.
Пусть математическая модель САУ имеет вид линейного дифференциального уравнения степени n с постоянными коэффициентами характеристический многочлен (собственный оператор) которого в общем виде записывается следующим образом
 . (3.1)
. (3.1)
Тогда условия для устойчивости систем регулирования описываемых линейными дифференциальными уравнениями определяются только видом (степенью и значениями коэффициентов). В частности, критерий Рауса для уравнений динамики до пятого порядка включительно записывается следующим образом:
1. Для уравнений первого порядка ( ) необходимым и достаточным условием устойчивости является положительность коэффициентов:
) необходимым и достаточным условием устойчивости является положительность коэффициентов:  > О;
> О; 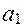 > О;
> О;
2. Для уравнений второго порядка ( ) необходимым и достаточным условием устойчивости является также положительность коэффициентов:
) необходимым и достаточным условием устойчивости является также положительность коэффициентов:  > О;
> О; 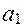 > О;
> О;  > О;
> О;
3. Для уравнений третьего порядка (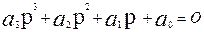 ) необходимым и достаточным условием устойчивости является положительность коэффициентов
) необходимым и достаточным условием устойчивости является положительность коэффициентов  > О;
> О; 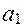 > О;
> О;  > О;
> О;  > О и выполнение неравенства
> О и выполнение неравенства
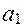
 -
- 
 > О.
> О.
4. Для уравнений четвертого порядка ( ) кроме положительности коэффициентов требуется выполнение неравенства
) кроме положительности коэффициентов требуется выполнение неравенства
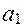 (
(
 -
- 
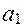 )-
)- 
 > О.
> О.
5.Для уравнений пятого порядка ( ) необходимым и достаточным условием устойчивости является положительность коэффициентов и еще два дополнительных неравенства
) необходимым и достаточным условием устойчивости является положительность коэффициентов и еще два дополнительных неравенства
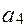
 -
- 
 > О.
> О.
(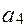
 -
- 
 )(
)(
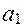 -
- 
 ) – (
) – (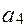
 -
- 
 )2 > О.
)2 > О.
Таким образом для уравнений первого и второго порядка необходимым и достаточным условием является положительность всех коэффициентов характеристического уравнения, а для уравнений высшего порядка накладываются дополнительные условия, выраженные соответствующими неравенствами.
Как следует из формулировки критерия Рауса сутью его применения для уравнений невысокого порядка является простая проверка выполнения соответствующих неравенств. В общем случае критерий Рауса формулируется в форме алгоритма с непростой последовательностью операций, что затрудняет его использование на практике.
Поэтому наибольшее распространение получил алгебраический критерий устойчивости, сформулированный в 1895 году математиком А.Гурвицом для исследования процессов регулирования турбин. Критерий Гурвица формулируется следующим образом.
Предположим, что исследуется система автоматического регулирования, описываемая дифференциальным уравнением n -го порядка и имеющего характеристическое уравнение вида (3.1).
Используя коэффициенты характеристического уравнения составим квадратичную матрицу, содержащую n строк и n столбцов:






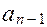

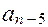 ... 0
... 0

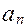

 ... 0
... 0
 0
0 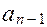
 ... 0
... 0
 D = 0
D = 0 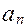
 ... 0
... 0
.......
0 0 0.. 0
 0 0 0...
0 0 0... 

Определитель D составляется следующим образом. По диагонали от левого верхнего до правого нижнего углов выписываются все коэффициенты характеристического уравнения (3.1) в порядке убывания от 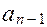 до
до  . Каждый столбец дополняется так, чтобы вниз от коэффициентов главной диагонали шли коэффициенты с увеличивающимся индексом, а вверх - с уменьшающимся индексом. В случае отсутствия коэффициента, а также если индекс его меньше нуля, или больше n, на его место пишется нуль. Обозначим главные миноры матрицы D через D n - 1,..., D 1. Эти миноры в определителе D выделены штриховыми линиями. Тогда критерий Гурвица формулируется следующим образом: для того, чтобы САУ была устойчивой, необходимо и достаточно, чтобы коэффициенты характеристического уравнения, определитель D и его главные миноры были положительными.
. Каждый столбец дополняется так, чтобы вниз от коэффициентов главной диагонали шли коэффициенты с увеличивающимся индексом, а вверх - с уменьшающимся индексом. В случае отсутствия коэффициента, а также если индекс его меньше нуля, или больше n, на его место пишется нуль. Обозначим главные миноры матрицы D через D n - 1,..., D 1. Эти миноры в определителе D выделены штриховыми линиями. Тогда критерий Гурвица формулируется следующим образом: для того, чтобы САУ была устойчивой, необходимо и достаточно, чтобы коэффициенты характеристического уравнения, определитель D и его главные миноры были положительными.
Следует отметить, что с увеличением степени характеристического уравнения САР вычисление определителей становится громоздким.
Раскрывая определители, фигурирующие в общей формулировке критерия устойчивости, можно получить частные критерии устойчивости, которые будут совпадать с формулами Рауса.
Необходимо обратить внимание, что в рассмотренных критериях требуется положительность коэффициентов. Положительность коэффициентов является необходимым условием устойчивости САУ.
Существенным недостатком критерия является то обстоятельство, что для уравнений высокого порядка вычисления матриц получаются достаточно громоздкими.
При этом в случае неустойчивой системы критерий не дает ответы на то, каким образом надо изменить параметры системы, чтобы сделать ее устойчивой. Это обстоятельство требует использования и других критериев, которые были бы более удобными в инженерной практике.
3.3.3. Частотные критерии Михайлова и Найквиста
Сущность критерия Михайлова заключается в следующем. Рассмотрим отдельно левую часть характеристического уравнения (3.1), которое представляет собой характеристический полином степени n:
 . (3.2)
. (3.2)
Подставим в этот полином чисто мнимую величину  , выделив при этом действительные и мнимые части. Тогда
, выделив при этом действительные и мнимые части. Тогда
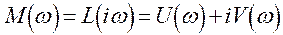 . (3.3)
. (3.3)
Очевидно, что вещественная часть будет содержать четные степени  , а мнимая - нечетные. Если значение частоты
, а мнимая - нечетные. Если значение частоты  менять от нуля до бесконечности, то вектор
менять от нуля до бесконечности, то вектор  опишет на комплексной плоскости (
опишет на комплексной плоскости ( ) некоторую кривую (годограф), которая называется годографом Михайлова. Практически кривая Михайлова строится по точкам, задаваясь значениями частоты
) некоторую кривую (годограф), которая называется годографом Михайлова. Практически кривая Михайлова строится по точкам, задаваясь значениями частоты  и вычисляя
и вычисляя  . Результаты расчетов сводятся в таблицу, по которой и строится затем кривая. Введенные выше понятия позволяют дать формулировку критерия в следующей наиболее простой форме: для устойчивости САР необходимо и достаточно, чтобы при изменении параметра
. Результаты расчетов сводятся в таблицу, по которой и строится затем кривая. Введенные выше понятия позволяют дать формулировку критерия в следующей наиболее простой форме: для устойчивости САР необходимо и достаточно, чтобы при изменении параметра  от нуля до бесконечности, кривая Михайлова последовательно пересекала оси координат (
от нуля до бесконечности, кривая Михайлова последовательно пересекала оси координат ( ) « n » раз, где n - степень характеристического полинома. Кривая Михайлова для устойчивых систем имеет плавную спиралевидную форму, причем конец ее уходит в бесконечность. Таким образом, для выполнения задания № 3, в части, касающейся оценки устойчивости по критерию Михайлова, следует построить кривую Михайлова и посчитать число ее пересечений с осями координат.
) « n » раз, где n - степень характеристического полинома. Кривая Михайлова для устойчивых систем имеет плавную спиралевидную форму, причем конец ее уходит в бесконечность. Таким образом, для выполнения задания № 3, в части, касающейся оценки устойчивости по критерию Михайлова, следует построить кривую Михайлова и посчитать число ее пересечений с осями координат.
Критерий Найквиста позволяет по виду амплитудно-фазовой частотной (АФЧХ) характеристики разомкнутой системы регулирования судить об ее устойчивости в замкнутом состоянии. Для его формулировки воспользуемся соотношением для передаточной функции разомкнутой системы регулирования, которое имеет вид:
 , (3.4)
, (3.4)
В соотношении (3..4)  -характеристический многочлен левой части линейного дифференциального уравнения САУ (собственный оператор),
-характеристический многочлен левой части линейного дифференциального уравнения САУ (собственный оператор),  -характеристический многочлен правой части (входной оператор). При подстановке
-характеристический многочлен правой части (входной оператор). При подстановке  в соотношение (3.4) и после выделения действительной и мнимой частей получим
в соотношение (3.4) и после выделения действительной и мнимой частей получим
 (3.5)
(3.5)
| <== предыдущая лекция | | | следующая лекция ==> |
| Тема 15 Особенности экономической мысли в России | | |
Не нашли, что искали? Воспользуйтесь поиском:
 Y
Y

