Теоретические характеристики насосов.

При подборе и эксплуатации насосов необходимо знать зависимости между основными их техническими показателями, которые отражают характеристику насоса.

Характеристика, построенная с помощью аналитических зависимостей, называется теоретической. Она показывает только качественную взаимосвязь, например, между напором и расходом. Для получения характеристик, отражающих количественную зависимость между основными рабочими параметрами, производят испытания реального насоса и только тогда, после обработки полученных результатов, строят рабочие характеристики.

Теоретические характеристики. Для получения теоретической характеристики H_T-Q_т рассматривается работа одноступенчатой машины при следующих допущениях:

1) машина идеальная, т.е. потери в ней отсутствуют;

2) число лопастей бесконечно большое;

3) вход жидкости в рабочее колесо радиальный ( ₁=90⁰);

4) машина в этом случае создает напор H_T и подает количество жидкости Q_T.

Используя соотношения из выходного параллелограмма скоростей (рис. 11), имеем C_2U=U₂-C_2R×ctg b₂, (44)

Рис. 11. Параллелограмм скоростей

а радиальная скорость на выходе из рабочего колеса насоса

С_2R= 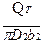(45)

Тогда уравнение Эйлера примет вид

H_T= =

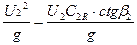
Окружная скорость U₂ может быть представлена как U₂=pD₂n

H_T= (46)

Величины D₂ и b₂ являются конструктивными элементами рабочего колеса и для данного насоса будут неизменными. Величины H_T, Q_T и n могут изменяться при выбранном угле b₂ в весьма широких пределах.

Рассмотрим случай, когда частота вращения n остаётся постоянной, а угол b₂ изменяется в пределах от b_{2 min} до b_{2 max}, т.е. составим функциональную зависимость H_T=f(Q_T) при n=const для различных форм лопастей определяемых углом b₂.

Обозначим 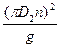=A; =В.

Тогда уравнение упрощается и принимает вид прямой:

H_T=A-ВQ_T ctgb₂ (47)

Таким образом, зависимость теоретического напора Н_т от теоретической подачи Q_т выражается уравнением первой степени, которое в координатах Q_т и Н_т графически изображается прямыми линиями; наклон этих прямых зависит от значения углового коэффициента, являющегося функцией угла b₂.

Так для угла b₂<90⁰ (лопастей, загнутых назад) будем иметь прямую с положительным угловым коэффициентом, так как ctg b₂>0. В этом случае с увеличением подачи напор уменьшится (прямая пойдёт вниз). Для угла b₂=90⁰ (радиальных лопастей), когда ctg b₂=0, напор с изменением подачи не меняется (прямая параллельна оси Q_T). А когда b₂>90⁰(для лопастей, загнутых вперёд) и ctg<0 получаем прямую с отрицательным угловым коэффициентом. Следовательно, с увеличением подачи напор растет (прямая идет вверх). Указанные характеристики изображены на рис. 12.

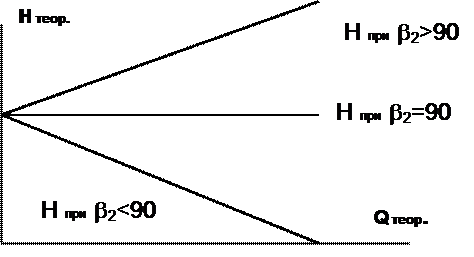
Рис. 12. Зависимости Q_теор.- H_теор.для различных выходных углов b₂

Согласно рис. 12, рабочие колеса с лопатками, загнутыми вперед b₂>90⁰, создают значительно больший напор, чем колеса с лопатками, загнутыми назад b₂<90⁰, и в этом их основное преимущество. Ввиду этого рабочие колеса центробежных насосов, используемых для нагнетания жидкостей, как правило, изготавливаются с лопатками, загнутыми назад.

При изменении частоты вращения изменяется ордината. Это значит, что пучок прямых переместится вверх (когда n растёт) или вниз (при уменьшении n). Полученная зависимость H_Tеор-Q_Tеор справедливо для всех лопастных машин (насосов, компрессорных машин, турбин).

Для получения действительной характеристики насоса необходимо внести поправки на гидравлические потери (в проточной части насоса), объемные и механические, а также на конечное число лопаток.

Теоретический напор при конечном числе лопаток H_T¢ будет меньше теоретического напора при бесконечном числе лопаток Н_T. Уменьшение теоретического напора учитывается поправочным коэффициентом k, значение которого меньше 1(прямая a), рис. 13.

Потери сопротивления протеканию жидкости при турбулентном движении практически можно считать пропорциональными квадрату подачи, т.е. h_п=SQ². Графически потери от трения в каналах изображаются квадратичной

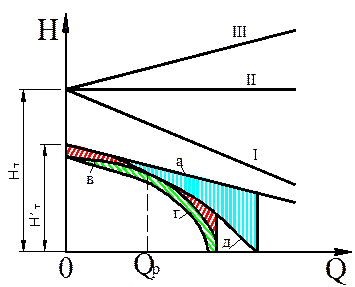параболой с вершиной в начале координат (кривая В). откладывая значения этих потерь вниз от линии а, получим кривую В.

Потери на удар при входе жидкости на лопатки или в направляющий аппарат вызываются резким изменением направления средней скорости.

Для каждого насоса существует оптимальный расход, который соответствует максимальному значению КПД насоса.

Рис. 13

При отклонении подачи Q_X от расчетной в ту или иную сторону появляются потери на удар, которые возрастают пропорционально квадрату подачи: h_уд=S₀(Q_X-Q_R)². Графически этому уравнению соответствует параболическая кривая с вершиной в точке безударного входа h_уд=0 при Q_x=Q_R (кривая В).

Учитывая утечки воды через зазоры, действительная характеристика Q-H (кривая Г ) несколько сместится влево. К механическим потерям относятся потери на трение дисков колеса о жидкость и потери трения в подшипниках и сальниках. Эти параметры практически не влияют на характеристику насоса.

Не нашли, что искали? Воспользуйтесь поиском: