
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Число обусл-ти матрицы и его св-ва. Хорошо обусл-е и плохо обусл-е СЛАУ. Геометрическая интерпретация понятия обусловленности.
Рассмотрим линейную алгебраическую систему, записанную в виде векторно-матричного уравнения Ах = b, (2.1), где А — невырожденная n ´ n -матрица коэффициентов данной системы; b — ненулевой n -мерный вектор свободных членов; х — n -мерный вектор неизвестных (решение).
Пусть правая часть (2.1) получила приращение («возмущение») D b, т.е. вместо истинного вектора b используется приближенный вектор b + D b. Реакцией решения х на возмущение D b правой части будет вектор поправок Ах, т.е. если х — решение (2.1), то х + D х — решение уравнения А(х + Dх) = b + Db. (2.2)
Понимая под абсолютной погрешностью приближенного вектора норму разности между точным и приближенным векторами, а под относительной погрешностью — отношение абсолютной погрешности к норме вектора (точного или приближенного), выясним связь между относительными погрешностями вектора свободных членов и вектора-решения. Иначе говоря, получим оценку вида  , где ||-|| — какая-либо векторная норма, а (?) — неизвестный пока коэффициент связи.
, где ||-|| — какая-либо векторная норма, а (?) — неизвестный пока коэффициент связи.
Подставляя (2.1) в (2.2), видим, что поправка D х связана с возмущением D b таким же, как и (2.1), равенством АDх = D b из которого находим ее явное выражение Dx = A-1Db. (2.3)
Нормируя равенства (2.1) и (2.3), будем иметь || b ||£|| A || || x || и ||D x ||£|| A-1 || ||D b ||, где матричная норма должна быть согласованной с выбранной векторной нормой. Эти два числовых неравенства одинакового смысла можно перемножить.
Из последнего делением на || b ||×|| х || получаем искомую связь 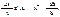 (2.4)
(2.4)
Положительное число  — коэффициент этой связи — называют числом (мерой) обусловленности матрицы А и обозначают cond А.
— коэффициент этой связи — называют числом (мерой) обусловленности матрицы А и обозначают cond А.
Легко показать, что то же самое число cond А =  служит коэффициентом роста относительных погрешностей при неточном задании элементов матрицы А в (2.1). А именно, если матрица А получила возмущение D А и х + D х — решение возмущенной системы (А + D A) (х + D х) = b, то справедливы неравенства
служит коэффициентом роста относительных погрешностей при неточном задании элементов матрицы А в (2.1). А именно, если матрица А получила возмущение D А и х + D х — решение возмущенной системы (А + D A) (х + D х) = b, то справедливы неравенства
 (2.5)
(2.5)
Итак, неравенства (2.4) и (2.5) показывают, что, чем больше число обусловленности, тем сильнее сказывается на решении линейной системы ошибка в исходных данных. Грубо говоря, если cond А = О( 10 р) и исходные данные имеют погрешность в l-м знаке после запятой, то независимо от способа решения системы (2.1) в результате можно гарантировать не более l-р знаков после запятой.
Если condA<10, то говорят, что СЛАУ хорошо обусловлена, то есть ошибки входных данных слабо влияют на решение. Если condA>103,то СЛАУ обусловлена плохо, что приводит к большим, но конечным изменениям в решении. Плохая обусловленность не следствие малости по сравнению с единицей определителя А и не оттого, что знаменатель мал или обратная матрица близка к 0, а за счёт появления в обратной матрице больших членов.
Если число cond А велико, то система считается плохо обусловленной.
Если используются подчиненные матричные нормы (для которых норма единичной матрицы есть единица), то, очевидно: cond А =  т.е. число обусловленности не может быть меньше 1. Можно также указать верхнюю границу для чисел обусловленности, превышение которой при решении линейных систем на конкретной ЭВМ может привести к заведомо ложным результатам. Так, решение считается ненадежным, если cond A ³ (macheps)-1 или даже cond A ³ ³ (macheps)0.5.
т.е. число обусловленности не может быть меньше 1. Можно также указать верхнюю границу для чисел обусловленности, превышение которой при решении линейных систем на конкретной ЭВМ может привести к заведомо ложным результатам. Так, решение считается ненадежным, если cond A ³ (macheps)-1 или даже cond A ³ ³ (macheps)0.5.
Классическим примером плохо обусловленной матрицы является так называемая матрица Гильберта  демонстрирующая катастрофическое возрастание числа обусловленности с ростом размерности. Так, уже при n = 8, cond H 8 > 1010 и обратная матрица
демонстрирующая катастрофическое возрастание числа обусловленности с ростом размерности. Так, уже при n = 8, cond H 8 > 1010 и обратная матрица 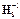 , полученная на машине с точностью представления чисел порядка 10-8, может не содержать ни одного верного знака.
, полученная на машине с точностью представления чисел порядка 10-8, может не содержать ни одного верного знака.
Очевидно, число обусловленности зависит от выбора матричной нормы (индуцированной, как правило, той или иной векторной нормой, в терминах которой характеризуется относительная погрешность решения алгебраической системы). Однако нетрудно получить оценку числа обусловленности через собственные числа матрицы. Действительно, пусть собственные числа li, матрицы А упорядочены по модулю: | l 1| ³ | l 2| ³ … ³ | ln |, т.е. спектральный радиус матрицы А есть r А = | l 1|. Тогда в силу известного неравенства r А £ || А || и соотношения между собственными числами прямой и обратной матриц, имеем  Оценкой снизу меры обусл-ти матрицы А служит величина
Оценкой снизу меры обусл-ти матрицы А служит величина 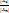 (называемая иногда числом обусдавленности Todda.) Для симметричных матриц эта оценка является числом обусл-ти, соотв-м спектральной норме матрицы.
(называемая иногда числом обусдавленности Todda.) Для симметричных матриц эта оценка является числом обусл-ти, соотв-м спектральной норме матрицы.
Геометр-ая трактовка понятия обусловл-ти. Плохая обусл-ть системы 2х ур-й с 2мя неизвестными означает, что прямые, являющиеся геом-ми образами ур-й, пересек-ся на координатной плоскости под очень острым углом => небольшое искажение в данных, т. е. параллельный перенос (при возмущении свободного члена) или поворот прямых (при возмущении матрицы коэфф-в), приводит к перемещению их точки пересечения, т.е. геометр-го образа решения.
 Октоэдр:
Октоэдр:  Эрмит:
Эрмит:  Рассм теперь произв прямоуг матрицу m*n A связ с нею лин преоб у =Ах. х — n -мерн вект-стб из n -мерн пр-ва R n, а у— m -мерн вект-стб из m -мерн пр-ва S m.
Введ в эт пр-вах нормы вект ||x||R и ||y||S. После этого норму прямоуг матрицы А опр рав-ом
Рассм теперь произв прямоуг матрицу m*n A связ с нею лин преоб у =Ах. х — n -мерн вект-стб из n -мерн пр-ва R n, а у— m -мерн вект-стб из m -мерн пр-ва S m.
Введ в эт пр-вах нормы вект ||x||R и ||y||S. После этого норму прямоуг матрицы А опр рав-ом  Норма т ´ n -матр А опр-ся как самой матр A, так и теми вект-ми нормами, кот вв в пр-вах R n и S m. При изм-ии этих норм изм-ся и норма матр.
Из опр-я нормы сл-ет соо: ||Ax||S £ ||A|| ||x||R
Для 2-х от т ´ n -матр Aи B при 1-м и том же опр-ии вект норм им соо ||A+B|| £ ||A||+||B|.Кроме того: ||lA|| £ ||l|| ||A| А для 2-х прямоуг матриц А и В: ||AB || £ || A || || B || Так для кубич вект норм пол-м матричн норму:
Норма т ´ n -матр А опр-ся как самой матр A, так и теми вект-ми нормами, кот вв в пр-вах R n и S m. При изм-ии этих норм изм-ся и норма матр.
Из опр-я нормы сл-ет соо: ||Ax||S £ ||A|| ||x||R
Для 2-х от т ´ n -матр Aи B при 1-м и том же опр-ии вект норм им соо ||A+B|| £ ||A||+||B|.Кроме того: ||lA|| £ ||l|| ||A| А для 2-х прямоуг матриц А и В: ||AB || £ || A || || B || Так для кубич вект норм пол-м матричн норму:  октоэдр:
октоэдр:  и для евклид нормы:
и для евклид нормы:  где r -макс хар-е число матр AAT.
8. Число обусл-ти матрицы и его св-ваРассм СЛА Ax=bпусть п.ч. получила приращ Δb т.е.вместо b исп-ся вект b+Δb.Реак реш x на возмущ Δb,будет вект поправок Ax и если x –реш сист,то (x+ Δx)-реш сист А(х+Dх)=b+DbВыясним связь м/у отн погр вект св чл-в и вект-реш. АDх =Dbи кот видим явное выраж: Ax = A-1Dbнормир:
||b|| ||Dx||£||A-1|| ||A|| ||Db|| ||x|| делим на ||b||* ||x|| и получаем:
где r -макс хар-е число матр AAT.
8. Число обусл-ти матрицы и его св-ваРассм СЛА Ax=bпусть п.ч. получила приращ Δb т.е.вместо b исп-ся вект b+Δb.Реак реш x на возмущ Δb,будет вект поправок Ax и если x –реш сист,то (x+ Δx)-реш сист А(х+Dх)=b+DbВыясним связь м/у отн погр вект св чл-в и вект-реш. АDх =Dbи кот видим явное выраж: Ax = A-1Dbнормир:
||b|| ||Dx||£||A-1|| ||A|| ||Db|| ||x|| делим на ||b||* ||x|| и получаем: 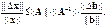 полож число ||A|| ||A-1||наз-ют числом обусл матр А
cond А =
полож число ||A|| ||A-1||наз-ют числом обусл матр А
cond А = 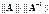 сл-т коэф роста отн погр-й, если х+Dх – реш возм сист (А+DA) (х +Dх) = b,то справ нер-ва
сл-т коэф роста отн погр-й, если х+Dх – реш возм сист (А+DA) (х +Dх) = b,то справ нер-ва
 Т.о.чем > число обусл.,тем сильнее сказ-ся на реш ЛС ошибка в исх данн. Если cond A велико,то сист счит плохо обусл. Числ обусл не м.б.>1. Реш счит ненадежн,если condA>=(macheps)-1 Примером плохо обусл матр счит матр Гильберта:
Т.о.чем > число обусл.,тем сильнее сказ-ся на реш ЛС ошибка в исх данн. Если cond A велико,то сист счит плохо обусл. Числ обусл не м.б.>1. Реш счит ненадежн,если condA>=(macheps)-1 Примером плохо обусл матр счит матр Гильберта:  при n=8 cond H8 > 10 и
при n=8 cond H8 > 10 и 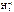 , получ на маш с точн предст чисел пор-ка 10-8, м. не соде-ть ни 1-го верного знака.
Прим.Матр коэф сист
, получ на маш с точн предст чисел пор-ка 10-8, м. не соде-ть ни 1-го верного знака.
Прим.Матр коэф сист 
 => cond А = 1101× 1011 = 1113111 >106. Учит в данн прим
=> cond А = 1101× 1011 = 1113111 >106. Учит в данн прим  пол-ем след оценку погр-ти реш:
пол-ем след оценку погр-ти реш:
 т.к.норма реш
т.к.норма реш  =1 то оценка абс погр||Dх||=||х|| dx £10.11 как видим реш возмущ сист впис в оценку ||х +Dх||£||х||+||Dх|| £ 1 + 10.01= 11.01.
Двум-й сл доп-ет прост гео тракт-ку пон-я обусл-ти. Плохая обусл сист 2-х ур с 2-мя неизв озн-ет, что прям, явл-ся гео образами ур-й, пересек-ся на коор-ой плоск-ти под оч острым углом. В этом сл небольш искаж в данн, интерпр-е как ||-ый перенос) или поворот прям, прив-т к знач-му перемещ их точки пересеч, т.е. гео-го образа реш.
19.Общ хар-ка ит мет реш. Схема ит мето-в
В сл больш разреж СЛАУ - ит методы, т. к. они, не прив к появл нов ненул эл-в и ок-ся более эф-ми по затратам маш t.
Схема. Q - неособенная кв-я матр, рассм как аппроксимация матр А, для кот реш сист Qu=dне предст особ труда. Матр Q наз-ют матр расщепл. Перепишем исх сист в виде Qx = (Q - A)x + b.
Постр ит-й проц Qx k +1=(Q - A) x k +b; k = 0.1,2,...
Разреш его отн-но x k+ l: x k +1=Q-1 (Q - A) x k +Q-1b,
или x k +1 = (E - Q-1A)x k +Q-1b.
Введ обознач: b = E - Q-1A; d = Q-1b.
Пол-м след ит схему: x k +1 = Bx k +d; k =0.1.2..
Это лини т схема 1-го пор-ка.
Т. Если ||B||<1, то ее ит схема сх-ся.Пусть ek – вект-погр-ти на k-ом шаге, а х* -точн реш.Тогда x k +1 =х* +е k +1, x k =х* +е k
х* +е k +1 = B(х* +е k)+dПоск-ку х* - точн реш, то
х*= Bх*+dПоэтому е k +1 = Bе k
е k = Bе k-1
е k +1 = B k +1е0 => ||е k +1|| £ ||B|| k +1|е0||.
При |В|| < 1 видно, что ||е k +1||
=1 то оценка абс погр||Dх||=||х|| dx £10.11 как видим реш возмущ сист впис в оценку ||х +Dх||£||х||+||Dх|| £ 1 + 10.01= 11.01.
Двум-й сл доп-ет прост гео тракт-ку пон-я обусл-ти. Плохая обусл сист 2-х ур с 2-мя неизв озн-ет, что прям, явл-ся гео образами ур-й, пересек-ся на коор-ой плоск-ти под оч острым углом. В этом сл небольш искаж в данн, интерпр-е как ||-ый перенос) или поворот прям, прив-т к знач-му перемещ их точки пересеч, т.е. гео-го образа реш.
19.Общ хар-ка ит мет реш. Схема ит мето-в
В сл больш разреж СЛАУ - ит методы, т. к. они, не прив к появл нов ненул эл-в и ок-ся более эф-ми по затратам маш t.
Схема. Q - неособенная кв-я матр, рассм как аппроксимация матр А, для кот реш сист Qu=dне предст особ труда. Матр Q наз-ют матр расщепл. Перепишем исх сист в виде Qx = (Q - A)x + b.
Постр ит-й проц Qx k +1=(Q - A) x k +b; k = 0.1,2,...
Разреш его отн-но x k+ l: x k +1=Q-1 (Q - A) x k +Q-1b,
или x k +1 = (E - Q-1A)x k +Q-1b.
Введ обознач: b = E - Q-1A; d = Q-1b.
Пол-м след ит схему: x k +1 = Bx k +d; k =0.1.2..
Это лини т схема 1-го пор-ка.
Т. Если ||B||<1, то ее ит схема сх-ся.Пусть ek – вект-погр-ти на k-ом шаге, а х* -точн реш.Тогда x k +1 =х* +е k +1, x k =х* +е k
х* +е k +1 = B(х* +е k)+dПоск-ку х* - точн реш, то
х*= Bх*+dПоэтому е k +1 = Bе k
е k = Bе k-1
е k +1 = B k +1е0 => ||е k +1|| £ ||B|| k +1|е0||.
При |В|| < 1 видно, что ||е k +1||  т.е.мет сх-ся к реш.
17.Мет ортогонализации
В алг док-ся,что всякую кв-ю невыр мат м.предст A=QR, где Q-ортог матр,а R-верхн Δ
QRx=b положим y=Rx
Qy=b
y=QTb
Rx=yб.рассм мет Хаусхолдера QR-разлож матр
21. Мет Якоби, Г-Зейделя реш СЛФУ
Мет Якоби: Предст A=A-+D+A+ тогда (A-+D + A+)x= b, Dx=-(A-+A+)x+ bзапишем ит процесс:
Dx k +1 = - (A- + A+)x k + b
x k +1 = - D-1 (A- + A+)x k + D-1 b, k = 0.1.... Здесь ит матр B = - D-1 (A- + A+)= -- D-1 (A – D)= (E –D-1A)
в коо форме:
т.е.мет сх-ся к реш.
17.Мет ортогонализации
В алг док-ся,что всякую кв-ю невыр мат м.предст A=QR, где Q-ортог матр,а R-верхн Δ
QRx=b положим y=Rx
Qy=b
y=QTb
Rx=yб.рассм мет Хаусхолдера QR-разлож матр
21. Мет Якоби, Г-Зейделя реш СЛФУ
Мет Якоби: Предст A=A-+D+A+ тогда (A-+D + A+)x= b, Dx=-(A-+A+)x+ bзапишем ит процесс:
Dx k +1 = - (A- + A+)x k + b
x k +1 = - D-1 (A- + A+)x k + D-1 b, k = 0.1.... Здесь ит матр B = - D-1 (A- + A+)= -- D-1 (A – D)= (E –D-1A)
в коо форме:  из 1-го ур сист отн-но 1-й из компон-т вект-ра. Из 1-го ур сист выр-ся х 1 и его знач прин-ся за знач х1 k +1 Из 2-го х 2 = х2 k +1 Перем п.ч. этих соо пол-ся=их знач на предыд ит-ии. Т.В сл диаг преоблАмет Якоби сх-ся.
Т. Мет Якоби(Гау-З) сх-ся к реш сист т.и т.т. когда все корни ур по модулю <1
из 1-го ур сист отн-но 1-й из компон-т вект-ра. Из 1-го ур сист выр-ся х 1 и его знач прин-ся за знач х1 k +1 Из 2-го х 2 = х2 k +1 Перем п.ч. этих соо пол-ся=их знач на предыд ит-ии. Т.В сл диаг преоблАмет Якоби сх-ся.
Т. Мет Якоби(Гау-З) сх-ся к реш сист т.и т.т. когда все корни ур по модулю <1  Мет Г-ЗЗапишем сист в виде(A-+D + A+)x= b
Ит схема Г-З также сл-ет из предст сист:
(A-+D)x k +1 = b- A+ x k, k= 0,1,.. или
Dx k +1 =b-A+ x k - A- x k +1, k= 0,1,.., => ст-й вид:
x k +1 =(A- +D)-1b- (A- +D) -1A+ x k, k= 0,1,...
что позвол-ет зап-ть ит матрицу и преобр ее
В=-(A- +D) -1A+ =- (A- +D) -1(A- D- A-)= E –(A- +D) -1A
Матрица расщепления Q= A- +D сод-т всю нижн Δ-ю часть матрицы А.Коо форма для сист общ вида:
Мет Г-ЗЗапишем сист в виде(A-+D + A+)x= b
Ит схема Г-З также сл-ет из предст сист:
(A-+D)x k +1 = b- A+ x k, k= 0,1,.. или
Dx k +1 =b-A+ x k - A- x k +1, k= 0,1,.., => ст-й вид:
x k +1 =(A- +D)-1b- (A- +D) -1A+ x k, k= 0,1,...
что позвол-ет зап-ть ит матрицу и преобр ее
В=-(A- +D) -1A+ =- (A- +D) -1(A- D- A-)= E –(A- +D) -1A
Матрица расщепления Q= A- +D сод-т всю нижн Δ-ю часть матрицы А.Коо форма для сист общ вида:
 Коо ф Г-З отлич от Я. тем,что 1-я Σ в п.ч. сод-т комп-ты вект реш-я не на k- й, на (k+ l) - й ит-ии. Т.Если в Адиаг преобл,мет Г-Зсх-ся быстрее,чем мет Я-би.
Сист Ах=вназ-ся норм-й, если А – симм полож опр.матр
Т. Если сист норм,то мет Зсх-ся
Т. Пусть detA¹0тогда сист АT А х = АTb норм-я.
22.Мет послед-й релаксации
Ит схема релаксации метода им-ет вид:
x k +1 =w[ D-1(b- A- x k +1 –A+ x k)]+(1 - w)x k, k= 0,1,..,
ит. матрица примет вид:
В = (D- wA- ) -1 [–wA+ +(1 - w)D]=E –(D/w- A- ) -1.
При wє(1;2) ит. схема наз-ся послед верх релакс и при wє(0;1) – послед нижней. Коо форма мет релакс им-ет вид:
Коо ф Г-З отлич от Я. тем,что 1-я Σ в п.ч. сод-т комп-ты вект реш-я не на k- й, на (k+ l) - й ит-ии. Т.Если в Адиаг преобл,мет Г-Зсх-ся быстрее,чем мет Я-би.
Сист Ах=вназ-ся норм-й, если А – симм полож опр.матр
Т. Если сист норм,то мет Зсх-ся
Т. Пусть detA¹0тогда сист АT А х = АTb норм-я.
22.Мет послед-й релаксации
Ит схема релаксации метода им-ет вид:
x k +1 =w[ D-1(b- A- x k +1 –A+ x k)]+(1 - w)x k, k= 0,1,..,
ит. матрица примет вид:
В = (D- wA- ) -1 [–wA+ +(1 - w)D]=E –(D/w- A- ) -1.
При wє(1;2) ит. схема наз-ся послед верх релакс и при wє(0;1) – послед нижней. Коо форма мет релакс им-ет вид:
 Для сх-ти проц необх,чтобы wє(0;2).
Т. Островского-Рейсадля норм систAx=bмет релакс сх-ся при люб х0 и любом wє(0;2).
23.Понятие о 2-х и 3-х слойных методах
Общ вид 2-х слойн мет-в:B k (x k +1 + x k ) = t k (A x k + b)
где B k - некот матр и t k - некот пар-р, завис от номера ит-ии.Выбор парам-в осущ-ют добив-сь удовл-я к-д требов-й(простота,легк стр-ра,легк обращ матриц B k и скаляров t k и как м.более быстр сх-ть х0 к реш х* .
Док-ся, если сист норм-я с изв гр-цами lmin>0, lmaх>0 спектра ее матр коэф,то при заранее фикс кол-ве ит-ий К мет б.обесп наим погр-ть,т.е. миним-ть вел ||х* - x k || в том сл,когда пар-ры t k вычисл по ф-ле
Для сх-ти проц необх,чтобы wє(0;2).
Т. Островского-Рейсадля норм систAx=bмет релакс сх-ся при люб х0 и любом wє(0;2).
23.Понятие о 2-х и 3-х слойных методах
Общ вид 2-х слойн мет-в:B k (x k +1 + x k ) = t k (A x k + b)
где B k - некот матр и t k - некот пар-р, завис от номера ит-ии.Выбор парам-в осущ-ют добив-сь удовл-я к-д требов-й(простота,легк стр-ра,легк обращ матриц B k и скаляров t k и как м.более быстр сх-ть х0 к реш х* .
Док-ся, если сист норм-я с изв гр-цами lmin>0, lmaх>0 спектра ее матр коэф,то при заранее фикс кол-ве ит-ий К мет б.обесп наим погр-ть,т.е. миним-ть вел ||х* - x k || в том сл,когда пар-ры t k вычисл по ф-ле  k=0,1,… а tk = cos
k=0,1,… а tk = cos  - корни полинома Чебышева.Совок этих ф-л наз-ют явн ит-м чебыш-ким набором пар-в
Рассм также 3-х слойн ит мет(в част-ти с чеб-ми пар-ми),связ-е уже не 2,а 3 приближения:х k +1,х k и х k -1
Такие мет явл-ся 2-х шаговыми.
27.Общ пост-ка зад на собств знач
Опр-ть собств знач l и собств знач р матр А такие, что Ар=lр, р≠0 det(A-lE)=0. Подставл li м.найти соо ему собств вект pi как реш сист (A-lE) p = 0. Задача опр-я собств знач и вект-в в ЧМ дел-ся на полн и частн задачу. При реш полн зад нах-т все собств знач,частн – часть,чаще всего наиб/наим собств знач.
Спектром матр А наз-ют мн-во всех его собств знач при реш полн зад,нах-ся весь спектр,а частн – некот его части.
Наряду с сист Ах=0б.рассм сопряж задачу АТх=0в сл действ матр А.А и АТ им-ют одинак спектры.
Сопряж зад на собств знач.р –собств вект А, q-собств вект АТ А*q = lq, q≠0
Вект pиq обл-т св-вом биортогон(р i, q j)=0, i±j – т.е.для вещ-й симм матр собств знач веществ,а собств вект ортогональны
28.Уст-ть задач на собств знач
Б.счит-ть,что все собст знач Апрост,пусть эл аij зад-ны с некот погр-ю.А м.предст-ть как (А + d А)и l,pудовл усл Ар = lр Тогда им-ем задачу:
(А + d Ар)(p + d p) = (l + dl)(р + d p)
или с точн-ю до 2-го пор-ка малости
А d p + d Ар = l d p + dl р
Рассм 2 сл: 1) d p = 0, dl ≠ 0 имеем d Ар i = dli р i Пусть q –собств вект для матр АТ отвеч собств знач l Тогда,умжнож это рав-во на q:
(q i, d Ар i) = dlI (q i, р i).=>
- корни полинома Чебышева.Совок этих ф-л наз-ют явн ит-м чебыш-ким набором пар-в
Рассм также 3-х слойн ит мет(в част-ти с чеб-ми пар-ми),связ-е уже не 2,а 3 приближения:х k +1,х k и х k -1
Такие мет явл-ся 2-х шаговыми.
27.Общ пост-ка зад на собств знач
Опр-ть собств знач l и собств знач р матр А такие, что Ар=lр, р≠0 det(A-lE)=0. Подставл li м.найти соо ему собств вект pi как реш сист (A-lE) p = 0. Задача опр-я собств знач и вект-в в ЧМ дел-ся на полн и частн задачу. При реш полн зад нах-т все собств знач,частн – часть,чаще всего наиб/наим собств знач.
Спектром матр А наз-ют мн-во всех его собств знач при реш полн зад,нах-ся весь спектр,а частн – некот его части.
Наряду с сист Ах=0б.рассм сопряж задачу АТх=0в сл действ матр А.А и АТ им-ют одинак спектры.
Сопряж зад на собств знач.р –собств вект А, q-собств вект АТ А*q = lq, q≠0
Вект pиq обл-т св-вом биортогон(р i, q j)=0, i±j – т.е.для вещ-й симм матр собств знач веществ,а собств вект ортогональны
28.Уст-ть задач на собств знач
Б.счит-ть,что все собст знач Апрост,пусть эл аij зад-ны с некот погр-ю.А м.предст-ть как (А + d А)и l,pудовл усл Ар = lр Тогда им-ем задачу:
(А + d Ар)(p + d p) = (l + dl)(р + d p)
или с точн-ю до 2-го пор-ка малости
А d p + d Ар = l d p + dl р
Рассм 2 сл: 1) d p = 0, dl ≠ 0 имеем d Ар i = dli р i Пусть q –собств вект для матр АТ отвеч собств знач l Тогда,умжнож это рав-во на q:
(q i, d Ар i) = dlI (q i, р i).=>
 вел
вел  наз-ся коэф перекоса матр А и по опр
w i =(cos ji)-1, где ji - угол м/у р и q
2) d p ≠ 0, dl = 0 здесь А d p + d Аp = l d pПред-м, что собств вект матр А обр-ют базис(они лин незав и их n) тогда d p=Σβpим-ем
наз-ся коэф перекоса матр А и по опр
w i =(cos ji)-1, где ji - угол м/у р и q
2) d p ≠ 0, dl = 0 здесь А d p + d Аp = l d pПред-м, что собств вект матр А обр-ют базис(они лин незав и их n) тогда d p=Σβpим-ем
 или
или  Поэтому
β=(q, dAp)/[(lj-lk)(qj,qk)]<=
(| qk || pj |*||dA||)/(| lj-lk |*(qk,pk))<=(ω/| lj-lk |)*||dA||
| d p |<=Σ|βj|*|pj|; |pj|=1,норм вект,то | d p |<=Σ|βj|
Выводы:1) Если погр-ть опр-я матр эл-в мала и мал i -й коэф перек, то мала и погр-ть опр-я i -го собств знач. 2) Если погр опр-я матр-х эл-в мала, малы все коэф перек и i -е собств знач простое, то мала и погр опр-я соо-го i -го собств вект.
для симм матр коэф перек =1 => зад нах-я собств знач устойчива. Если все ее собств знач простые,то уст-ва задача нах-я собств вект-в.
35.Мет вращений реш симм полн проблемы соб значИсп-ем след св-ва:1) Пусть {l, х} — соб пара матр В = С-1АС. Тогда {l, Cх} соб пара матр А. т.е. преобр-е подобия сохр неизм спектр любой матр 2). Пусть А – n×n-матр прост стр-ры, а матр L= diag(l i) и X = (x1;...; х n) обр-ны из ее соб-х чисел и соб-х вект соо-но. Тогда справ-во рав-во L = X-1AX. Или если явл-ся {l i, e i,} соб парой матр L= diag(l i)=X-1AX, то {l i, x i,} есть соб-я пара матр А.
Далее рассм-ем только симм веществ матр,кот им-ют ортонорм сист собств вект-в.Б.исп-ть след рав-во:
L = XTAXзн-т,для вся симм матр Анайд-ся диаг матр Lей ортог-но подобная.Б.исп-ть преоб с пом матр плоских вращений.
Поэтому
β=(q, dAp)/[(lj-lk)(qj,qk)]<=
(| qk || pj |*||dA||)/(| lj-lk |*(qk,pk))<=(ω/| lj-lk |)*||dA||
| d p |<=Σ|βj|*|pj|; |pj|=1,норм вект,то | d p |<=Σ|βj|
Выводы:1) Если погр-ть опр-я матр эл-в мала и мал i -й коэф перек, то мала и погр-ть опр-я i -го собств знач. 2) Если погр опр-я матр-х эл-в мала, малы все коэф перек и i -е собств знач простое, то мала и погр опр-я соо-го i -го собств вект.
для симм матр коэф перек =1 => зад нах-я собств знач устойчива. Если все ее собств знач простые,то уст-ва задача нах-я собств вект-в.
35.Мет вращений реш симм полн проблемы соб значИсп-ем след св-ва:1) Пусть {l, х} — соб пара матр В = С-1АС. Тогда {l, Cх} соб пара матр А. т.е. преобр-е подобия сохр неизм спектр любой матр 2). Пусть А – n×n-матр прост стр-ры, а матр L= diag(l i) и X = (x1;...; х n) обр-ны из ее соб-х чисел и соб-х вект соо-но. Тогда справ-во рав-во L = X-1AX. Или если явл-ся {l i, e i,} соб парой матр L= diag(l i)=X-1AX, то {l i, x i,} есть соб-я пара матр А.
Далее рассм-ем только симм веществ матр,кот им-ют ортонорм сист собств вект-в.Б.исп-ть след рав-во:
L = XTAXзн-т,для вся симм матр Анайд-ся диаг матр Lей ортог-но подобная.Б.исп-ть преоб с пом матр плоских вращений.
 Она получ-я из ед-й матр заменой 2-х единиц и 2-х нулей на пересеч i -х и j -х строк и стб числами с и ± s, такими,что c 2 +s 2 = 1.
Усл нор-ки позв-ет интерпр-ть числа с и s как cos и sin некот угла а, и умнож любой матр на матр Т ij изм-ет у нее т. 2 строки и 2 стб по ф-лам поворота на угол а в пл-ти, опред-й выбр-ой парой индексов.
Матр Т ij ортог при люб i j Î {1,.., n }=>матр
Она получ-я из ед-й матр заменой 2-х единиц и 2-х нулей на пересеч i -х и j -х строк и стб числами с и ± s, такими,что c 2 +s 2 = 1.
Усл нор-ки позв-ет интерпр-ть числа с и s как cos и sin некот угла а, и умнож любой матр на матр Т ij изм-ет у нее т. 2 строки и 2 стб по ф-лам поворота на угол а в пл-ти, опред-й выбр-ой парой индексов.
Матр Т ij ортог при люб i j Î {1,.., n }=>матр  подобна А,т.е. имеет тот же набор соб-х чисел.
Класс ит-й мет вращ-й, предп-ет постр-е посл-ти матр
B0(=A), B1, B2,...,B k,... такой, что на k -м шаге обн-ся max-й по мод эл-т матр B k- 1 предыд шага Нужн пов-е опр-ся: B k ->Lпри k->∞ Алг-м:0)выбир ключ эл-т матр А1) Вычисл р = 2 aij, q = aii – ajj,
подобна А,т.е. имеет тот же набор соб-х чисел.
Класс ит-й мет вращ-й, предп-ет постр-е посл-ти матр
B0(=A), B1, B2,...,B k,... такой, что на k -м шаге обн-ся max-й по мод эл-т матр B k- 1 предыд шага Нужн пов-е опр-ся: B k ->Lпри k->∞ Алг-м:0)выбир ключ эл-т матр А1) Вычисл р = 2 aij, q = aii – ajj,  .
2) Если q ≠ 0, то r^\q/(2d),
.
2) Если q ≠ 0, то r^\q/(2d), 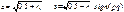 (если |p|<<|q|,то лучше s:=|p|-sigp ((pq)/(2cd)), если же q = 0, то c = s:=cos 45
3) Выч-ют новые диагональные элементы
(если |p|<<|q|,то лучше s:=|p|-sigp ((pq)/(2cd)), если же q = 0, то c = s:=cos 45
3) Выч-ют новые диагональные элементы
 .
4) Пол-ют bij = bji= 0 (или для контроля выч-ют
.
4) Пол-ют bij = bji= 0 (или для контроля выч-ют  ).
5) При m = 1,.., n,таких?что т≠i, т≠j, выч-ют изм-ся внедиаг эл-ты:
bim = bmi= cami + samj, bjm = bmj= - sami + camj.
6) Для всех ост пар инд-в т, l принимают bml = aml.
39. Преобразование Хаусхолдера.
Пусть ω-некот вект,такой,что ||ω||=(w,w)^1/2=(wTw)^1/2=1 постр преобр Х.
H=E-2wwT // wTw – матр wwT – число
Св-ва преобр:возьмем произв вект х и рассм у=Hx= (E-2wwT)=x-2w(w,x)Рассм 2 случая:1)Пусть вект х коллинеарен и х||w т.е. х=αw (альфа) Пол-м: y=x-2w(w,αw)=x-2 αw= αw-2 αw=- αw=-x //вект развор-ся в др сторону. 2) х ортог w <=> (x,w)=0 y=x Преоб Х. наз-ют преоб отраж-я, а матр Н – матр отраж-я.
3)Матр Х-ра симм: HT=(E-2wwT)T=E-2(wT)T wT= E-2wwT=H
4)Матр Х-ра ортог: H HT= H2=(E-2wwT)2=E2 – 4EwwT+4w(wTw)wT=E-4wwT+4wwT=E
HT= H-1=H
Ортог матр порожд-т изометрию. Изометрия - преобр,кот не меняет длин вект и углов м/у ними.
5) ||y||=||Hx||=||x||
Т.Если матр Х-ра Н стр-ть с пом вект-ра w=μ(x1-β,x2 …, xn) где β=sign(-x1)* [(Σxi)^1/2] если х ≠0
β=[(Σxi)^1/2], если х=0
μ=1/[(2 β^2 - 2β x1)^1/2]
Отличн от нуля вект х=(x1,…, xn) с пом матр Н преобр-ся в вект с нулев компон-ми,кроме 1-й, кот = β
y=Hx=(β,0,…,0)
Применим эту теор для постр матр Q, кот приводит задан матр А к верх Δ виду,т.е. А=QR Алг-м:
1) в кач-ве вект х возьмем 1-й стб матр А х=(a11,…, an1)Tи постр матр H1=E-2w1w1T где w1=μ (a11-β1, a21, …, an1)T прим-в его к матр Амы пол-м A1=H1A с пом этой матр преоб 1-й стб
=(β1 a12(1) … a1n(1))//верх строка матр
(0 a22(1) … a2n(1))//далее также преобр-е
(…………………………..)// Х-ра но для нижн части матр
(0 an2(1) … ann(1))
2)Рассм матр А с волной,получ из матр А,вычерк 1-й строки и 1-го стб. Постр матр H2=E-2w2w2Tматр H2 б.иметь вид: (1 0 … 0)
(0 * … *)
(… …… ….)
(0 * … *)
При умнож такой матр на матр АТ её 1-я строка и 1-й стб не изм-ся. A2=H1A1= H2 H1А=(β1 a12(1) … a1n(1))
(0 β2 … a2n(2))
(……0 a33(2)… a3n(2)))
(0…0 an3(2)… ann(2)))
Справ след теор: Т.Преоб Х-ра люб кв-я матр с действ эл-ми м.б. предст в виде произв ортог и верх Δ-й матр.
).
5) При m = 1,.., n,таких?что т≠i, т≠j, выч-ют изм-ся внедиаг эл-ты:
bim = bmi= cami + samj, bjm = bmj= - sami + camj.
6) Для всех ост пар инд-в т, l принимают bml = aml.
39. Преобразование Хаусхолдера.
Пусть ω-некот вект,такой,что ||ω||=(w,w)^1/2=(wTw)^1/2=1 постр преобр Х.
H=E-2wwT // wTw – матр wwT – число
Св-ва преобр:возьмем произв вект х и рассм у=Hx= (E-2wwT)=x-2w(w,x)Рассм 2 случая:1)Пусть вект х коллинеарен и х||w т.е. х=αw (альфа) Пол-м: y=x-2w(w,αw)=x-2 αw= αw-2 αw=- αw=-x //вект развор-ся в др сторону. 2) х ортог w <=> (x,w)=0 y=x Преоб Х. наз-ют преоб отраж-я, а матр Н – матр отраж-я.
3)Матр Х-ра симм: HT=(E-2wwT)T=E-2(wT)T wT= E-2wwT=H
4)Матр Х-ра ортог: H HT= H2=(E-2wwT)2=E2 – 4EwwT+4w(wTw)wT=E-4wwT+4wwT=E
HT= H-1=H
Ортог матр порожд-т изометрию. Изометрия - преобр,кот не меняет длин вект и углов м/у ними.
5) ||y||=||Hx||=||x||
Т.Если матр Х-ра Н стр-ть с пом вект-ра w=μ(x1-β,x2 …, xn) где β=sign(-x1)* [(Σxi)^1/2] если х ≠0
β=[(Σxi)^1/2], если х=0
μ=1/[(2 β^2 - 2β x1)^1/2]
Отличн от нуля вект х=(x1,…, xn) с пом матр Н преобр-ся в вект с нулев компон-ми,кроме 1-й, кот = β
y=Hx=(β,0,…,0)
Применим эту теор для постр матр Q, кот приводит задан матр А к верх Δ виду,т.е. А=QR Алг-м:
1) в кач-ве вект х возьмем 1-й стб матр А х=(a11,…, an1)Tи постр матр H1=E-2w1w1T где w1=μ (a11-β1, a21, …, an1)T прим-в его к матр Амы пол-м A1=H1A с пом этой матр преоб 1-й стб
=(β1 a12(1) … a1n(1))//верх строка матр
(0 a22(1) … a2n(1))//далее также преобр-е
(…………………………..)// Х-ра но для нижн части матр
(0 an2(1) … ann(1))
2)Рассм матр А с волной,получ из матр А,вычерк 1-й строки и 1-го стб. Постр матр H2=E-2w2w2Tматр H2 б.иметь вид: (1 0 … 0)
(0 * … *)
(… …… ….)
(0 * … *)
При умнож такой матр на матр АТ её 1-я строка и 1-й стб не изм-ся. A2=H1A1= H2 H1А=(β1 a12(1) … a1n(1))
(0 β2 … a2n(2))
(……0 a33(2)… a3n(2)))
(0…0 an3(2)… ann(2)))
Справ след теор: Т.Преоб Х-ра люб кв-я матр с действ эл-ми м.б. предст в виде произв ортог и верх Δ-й матр.