
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Теми практичних занять
О.М. Моргун, А.П. Марченко
Збірник
Практичних занять
НАВЧАЛЬНОЇ ДИСЦИПЛІНИ
«Інформаційне забезпечення діяльності підрозділів цивільного захисту »
підготовки фахівців освітньо-кваліфікаційного рівня "бакалавр"
у галузі знань 1702 "Цивільна безпека" за напрямом
6.170203 „Пожежна безпека”.
Черкаси 2013
Зміст
Практичне заняття. 3
Заняття № 1.1. Стандартні засоби розв’язання математичних задач. 5
Практичне заняття. 11
Заняття № 1.2. Розв’язання задач прогнозування. 12
Практичне заняття. 16
Заняття № 1.3. Розв’язання задач лінійного програмування. 17
Практичне заняття. 23
Заняття № 1.4. Розрахунок сил та засобів для проведення рятувальних робіт в середовищі MS Excel. 24
Практичне заняття. 34
Заняття № 1.5. Оцінка рівня фізичної підготовки рятувальників. 34
Практичне заняття. 37
Заняття № 2.1. Створення графічного матеріалу на основі графічних примітивів за допомогою MS Visio 38
Питання до заліку з дисципліни. 43
Теми практичних занять
| № з/п | Назва теми | Кількість годин |
| Змістовий модуль 1. Розв’язання практичних обчислювальних задач цивільного захисту. | ||
| 1. | Стандартні засоби розв’язання математичних задач. | |
| 2. | Розв’язання задач прогнозування. | |
| 3. | Розв’язання задач лінійного програмування. | |
| 4. | Розрахунок сил та засобів для проведення рятувальних робіт. | |
| 5. | Оцінка рівня фізичної підготовки рятувальників. | |
| Змістовий модуль 2. Сучасні інформаційні технології обробки даних. | ||
| 6. | Створення графічного матеріалу на основі графічних примітивів за допомогою MS Visio. | |
| 7. | Модульна контрольна робота №1. | |
| 8. | Залік. | |
| Разом: |
Самостійна робота
| № з/п | Назва теми | Кількість годин |
| 1. | Стандартні засоби розв’язання математичних задач. | |
| 2. | Розв’язання задач прогнозування та оптимізації. | |
| 3. | Розв’язання задач лінійного програмування. | |
| 4. | Розрахунок сил та засобів для проведення рятувальних робіт. | |
| 5. | Оцінка рівня фізичної підготовки рятувальників. | |
| 6. | Створення графічного матеріалу на основі графічних примітивів за допомогою MS Visio. | |
| Разом: |
Державна служба України з надзвичайних ситуацій
ЧЕРКАСЬКИЙ ІНСТИТУТ ПОЖЕЖНОЇ БЕЗПЕКИ ІМЕНІ ГЕРОЇВ ЧОРНОБИЛЯ
Кафедра вищої математики та інформаційних технологій
ЗАТВЕРДЖУЮ
Начальник кафедри
ВМ та ІТ
к.ф-м.н., доц.,
полковник с.ц.з.
_______ І.П. Частоколенко
“___”______2013р.
Навчальна дисципліна: Інформаційне забезпечення діяльності підрозділів цивільного захисту
4-й курс (стаціонар, курсанти).
МЕТОДИЧНА РОЗРОБКА
на проведення практичного заняття по темі № 1.1: «Стандартні засоби розв’язання математичних задач»
Час: 11 годин, з них 6 годин практичних занять, 5 годин самостійної роботи.
Тема 1.1: Стандартні засоби розв’язання математичних задач.
Мета заняття: освоїти методи та засоби розв'язування задачі підбору параметра засобами Microsoft Excel.
Метод проведення: практичне заняття.
Місце проведення: ауд. № 317, ауд. № 318.
Час проведення: 6 годин
Матеріально-технічне забезпечення: ПК.
Методичну розробку підготував
Викладач кафедри ВМ та ІТ А.П. Марченко
Методична розробка обговорена та схвалена на засіданні кафедри
Протокол №____від “__”________2013р.
Практичне заняття
Заняття № 1.1. Стандартні засоби розв’язання математичних задач.
Мета: освоїти методи та засоби розв'язування задачі підбору параметра засобами Microsoft Excel.
Завдання:
1. Ознайомитися з завданням та рекомендаціями по його виконанню.
2. Виконати на комп'ютері задачу підбору параметра засобами MS Excel відповідно до послідовності виконання роботи, приведеної нижче.
3. Виконати індивідуальне завдання за своїм варіантом. Варіант обирається за номером у журналі.
4. Результати роботи представити викладачу у вигляді звіту.
Послідовність виконання роботи:
1. Постановка задачі
Задачею підбору параметра називається знаходження такого значення аргумента даної функції, при якому ця функція набуває заданого значення.
Зокрема, це може бути пошук коренів заданого рівняння f(x)=0, коли необхідно знайти такі значення аргумента, за яких функція набуває нульового значення.
Розглянемо задачу знаходження коренів рівняння  . Якщо
. Якщо  має простий вигляд, то корені можна знайти аналітичним методом, тобто за формулами:
має простий вигляд, то корені можна знайти аналітичним методом, тобто за формулами:
q при  маємо лінійне рівняння
маємо лінійне рівняння  , корінь якого
, корінь якого 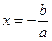 ;
;
q при  маємо квадратне рівняння
маємо квадратне рівняння  , дійсні корені якого
, дійсні корені якого  .
.
Але у більш складних випадках формул для обчислення коренів рівняння  не існує. Тому застосовують наступну чисельну методику:
не існує. Тому застосовують наступну чисельну методику:
q спочатку здійснюють відокремлення всіх коренів, тобто на заданому широкому проміжку  для кожного кореня знаходять досить вузький проміжок
для кожного кореня знаходять досить вузький проміжок  , на якому відсутні інші корені;
, на якому відсутні інші корені;
q уточнюють корені, тобто на кожному з вузьких проміжків знаходять значення кореня із заданою точністю.
Розглянемо відокремлення коренів. Основні методи відокремлення коренів: графічний та табличний.
У відповідності з графічним методом необхідно побудувати графік заданої функції  на всьому заданому проміжку
на всьому заданому проміжку  , після чого візуально локалізувати точки його перетину з віссю Ox. Далі в околі точок перетину треба довільним способом вибрати вузькі проміжки
, після чого візуально локалізувати точки його перетину з віссю Ox. Далі в околі точок перетину треба довільним способом вибрати вузькі проміжки  так, щоб на кожному з них знаходилась лише одна точка перетину графіка з віссю. Один із недоліків даного методу – його громіздкість. Другий недолік – ненадійність – пов’язаний з можливістю втратити корені при неякісній побудові графіка.
так, щоб на кожному з них знаходилась лише одна точка перетину графіка з віссю. Один із недоліків даного методу – його громіздкість. Другий недолік – ненадійність – пов’язаний з можливістю втратити корені при неякісній побудові графіка.
Більш зручним слід вважати табличний метод, оскільки він досить формальний і зводиться до послідовності простих обчислювальних операцій. У відповідності з цим методом, на всьому широкому проміжку  визначають знаки функції
визначають знаки функції  з певним кроком h. З одержаної таблиці знаків вибирають вузькі проміжки
з певним кроком h. З одержаної таблиці знаків вибирають вузькі проміжки  , на кінцях яких функція має протилежні знаки. Чим дрібніший крок h, тим надійніше будуть відокремлені корені, тим менша ймовірність їх втратити.
, на кінцях яких функція має протилежні знаки. Чим дрібніший крок h, тим надійніше будуть відокремлені корені, тим менша ймовірність їх втратити.
2. Приклад розв’язання рівняння
Відокремимо корені рівняння 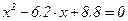 на широкому проміжку
на широкому проміжку  . Виберемо крок
. Виберемо крок  . При цьому ми припускаємо, що відстань між найближчими коренями даного рівняння перевищує вибраний крок, і тому корені втрачені не будуть. Складемо таблицю знаків функції
. При цьому ми припускаємо, що відстань між найближчими коренями даного рівняння перевищує вибраний крок, і тому корені втрачені не будуть. Складемо таблицю знаків функції 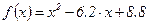 на проміжку
на проміжку  .
.
| x | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | 5.0 |
| Знак f(x) | + | + | + | – | – | – | + | + |
Таким чином, таблиця показує, що на широкому проміжку  знаходяться два корені: перший – в межах вузького проміжка
знаходяться два корені: перший – в межах вузького проміжка  , другий – в межах вузького проміжка
, другий – в межах вузького проміжка  .
.
Подібну таблицю для заданої функції  можна скласти засобами MS Excel. Для цього достатньо знати широкий проміжок
можна скласти засобами MS Excel. Для цього достатньо знати широкий проміжок  , а також правильно вибрати крок побудови таблиці h.
, а також правильно вибрати крок побудови таблиці h.
І. Виконуємо побудову таблиці значень заданої функції на широкому проміжку [A,B] з кроком h =0,5.
ІІ. Визначаємо вузькі проміжки, де знаходяться корені (на кінцях цього проміжку функція f(x) має протилежні знаки). Виділяємо кінці таких проміжків шрифтом – полужирний курсив.
ІІІ. Для уточнення коренів в MS Excel використовують підбір параметрів. При цьому порядок дій для кожного вузького проміжка  може бути наступним:
може бути наступним:
¨ Вибрати комірки для розміщення значення аргумента x і функції y (наприклад, F4 і F5 відповідно).
¨ В комірку F4 ввести орієнтовне значення кореня. Це має бути один із кінців вузького проміжка  .
.
¨ В комірку F5 ввести формулу для обчислення значення функції  , вважаючи, що аргумент x знаходиться в комірці F4.
, вважаючи, що аргумент x знаходиться в комірці F4.
¨ Виконати команду Сервис-Подбор параметра.... Внаслідок цього на екрані з’являється діалогове вікно Подбор параметра.
¨ В поле Установить в ячейке: ввести адресу комірки значення функції, тобто F5.
¨ В поле Значение: ввести нульове значення.
¨ В поле Изменяя значение ячейки: ввести адресу комірки значення аргумента, тобто F4.
¨ Натиснути кнопку OK діалогового вікна. З’являється нове вікно Результат подбора параметра, в якому повідомляється, вдалося чи ні розв’язати рівняння.
¨ Значення кореня рівняння з’являється у комірці F4.
Таким чином, ми отримуємо наступні результати:
¨ на проміжку [2;2,5] корінь знаходиться в точці x =2,2;
¨ на проміжку [3,5;4,5] корінь знаходиться в точці x =4.
Якщо користувача не задовольняє точність знайденого значення, то він може її змінити. Для цього треба виконати команду Сервис-Параметры..., у діалоговому вікні Параметры вибрати вкладинку Вычисления, а полі Относительная погрешность: цієї вкладинки ввести інше значення (наприклад, 0.00001 замість 0.001).
Приклад оформлення
| Завдання №3. Розв'язування рівняння | |||||

| |||||
| Рівняння: | |||||
| Таблиця значень: | Корені: | ||||
| i | x | y | |||
| -10 | 304,7000 | 1) x = | 1,9347 | ||
| -9,5 | 280,5000 | y = | 0,0000 | ||
| -9 | 257,3000 | ||||
| -8,5 | 235,1000 | 2) x = | 2,7653 | ||
| -8 | 213,9000 | y = | 0,0000 | ||
| -7,5 | 193,7000 | ||||
| -7 | 174,5000 | ||||
| -6,5 | 156,3000 | ||||
| -6 | 139,1000 | ||||
| -5,5 | 122,9000 | ||||
| -5 | 107,7000 | ||||
| -4,5 | 93,5000 | ||||
| -4 | 80,3000 | ||||
| -3,5 | 68,1000 | ||||
| -3 | 56,9000 | ||||
| -2,5 | 46,7000 | ||||
| -2 | 37,5000 | ||||
| -1,5 | 29,3000 | ||||
| -1 | 22,1000 | ||||
| -0,5 | 15,9000 | ||||
| 10,7000 | |||||
| 0,5 | 6,5000 | ||||
| 3,3000 | |||||
| 1,5 | 1,1000 | ||||
| -0,1000 | |||||
| 2,5 | -0,3000 | ||||
| 0,5000 | |||||
| 3,5 | 2,3000 | ||||
| 5,1000 | |||||
| 4,5 | 8,9000 | ||||
| 13,7000 | |||||
| 5,5 | 19,5000 | ||||
| 26,3000 | |||||
| 6,5 | 34,1000 | ||||
| 42,9000 | |||||
| 7,5 | 52,7000 | ||||
| 63,5000 | |||||
| 8,5 | 75,3000 | ||||
| 88,1000 | |||||
| 9,5 | 101,9000 | ||||
| 116,7000 |
| Таблиця значень у вигляді формул: | Корені: | ||||
| i | x | y | |||
| -10 | =2*B6^2-9,4*B6+10,7 | 1) x = | 1,93490499648135 | ||
| -9,5 | =2*B7^2-9,4*B7+10,7 | y = | =2*F6^2-9,4*F6+10,7 | ||
| -9 | =2*B8^2-9,4*B8+10,7 | ||||
| -8,5 | =2*B9^2-9,4*B9+10,7 | 2) x = | 2,76564268442471 | ||
| -8 | =2*B10^2-9,4*B10+10,7 | y = | =2*F9^2-9,4*F9+10,7 | ||
| -7,5 | =2*B11^2-9,4*B11+10,7 | ||||
| -7 | =2*B12^2-9,4*B12+10,7 | ||||
| -6,5 | =2*B13^2-9,4*B13+10,7 | ||||
| -6 | =2*B14^2-9,4*B14+10,7 | ||||
| -5,5 | =2*B15^2-9,4*B15+10,7 | ||||
| -5 | =2*B16^2-9,4*B16+10,7 | ||||
| -4,5 | =2*B17^2-9,4*B17+10,7 | ||||
| -4 | =2*B18^2-9,4*B18+10,7 | ||||
| -3,5 | =2*B19^2-9,4*B19+10,7 | ||||
| -3 | =2*B20^2-9,4*B20+10,7 | ||||
| -2,5 | =2*B21^2-9,4*B21+10,7 | ||||
| -2 | =2*B22^2-9,4*B22+10,7 | ||||
| -1,5 | =2*B23^2-9,4*B23+10,7 | ||||
| -1 | =2*B24^2-9,4*B24+10,7 | ||||
| -0,5 | =2*B25^2-9,4*B25+10,7 | ||||
| =2*B26^2-9,4*B26+10,7 | |||||
| 0,5 | =2*B27^2-9,4*B27+10,7 | ||||
| =2*B28^2-9,4*B28+10,7 | |||||
| 1,5 | =2*B29^2-9,4*B29+10,7 | ||||
| =2*B30^2-9,4*B30+10,7 | |||||
| 2,5 | =2*B31^2-9,4*B31+10,7 | ||||
| =2*B32^2-9,4*B32+10,7 | |||||
| 3,5 | =2*B33^2-9,4*B33+10,7 | ||||
| =2*B34^2-9,4*B34+10,7 | |||||
| 4,5 | =2*B35^2-9,4*B35+10,7 | ||||
| =2*B36^2-9,4*B36+10,7 | |||||
| 5,5 | =2*B37^2-9,4*B37+10,7 | ||||
| =2*B38^2-9,4*B38+10,7 | |||||
| 6,5 | =2*B39^2-9,4*B39+10,7 | ||||
| =2*B40^2-9,4*B40+10,7 | |||||
| 7,5 | =2*B41^2-9,4*B41+10,7 | ||||
| =2*B42^2-9,4*B42+10,7 | |||||
| 8,5 | =2*B43^2-9,4*B43+10,7 | ||||
| =2*B44^2-9,4*B44+10,7 | |||||
| 9,5 | =2*B45^2-9,4*B45+10,7 | ||||
| =2*B46^2-9,4*B46+10,7 |
Примітка. Таблиця значень у вигляді формул отримується в табличному процесорі MS Excel за допомогою команди Сервис-Параметры, а у вікні Параметры вибрати вкладку Вид, де задати прапорець Формулы.
Збірник варіантів завдання
Розв’язати задане нелінійне рівняння  , знайшовши всі його корені на проміжку [-10, 10].
, знайшовши всі його корені на проміжку [-10, 10].
Варіант 1.  . Варіант 2.
. Варіант 2.  .
.
Варіант 3.  . Варіант 4.
. Варіант 4.  .
.
Варіант 5.  . Варіант 6.
. Варіант 6.  .
.
Варіант 7.  . Варіант 8.
. Варіант 8.  .
.
Варіант 9.  . Варіант 10.
. Варіант 10.  .
.
Варіант 11.  . Варіант 12.
. Варіант 12.  .
.
Варіант 13.  . Варіант 14.
. Варіант 14.  .
.
Варіант 15.  . Варіант 16.
. Варіант 16.  .
.
Варіант 17.  . Варіант 18.
. Варіант 18.  .
.
Варіант 19.  . Варіант 20.
. Варіант 20.  .
.
Варіант 21.  . Варіант 22.
. Варіант 22.  .
.
Варіант 23. 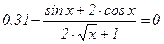 . Варіант 24.
. Варіант 24.  .
.
Варіант 25.  . Варіант 26.
. Варіант 26.  .
.
Варіант 27.  . Варіант 28.
. Варіант 28.  .
.
Варіант 29.  . Варіант 30.
. Варіант 30.  .
.
Варіант 31.  . Варіант 32.
. Варіант 32.  .
.
Варіант 33.  . Варіант 34.
. Варіант 34.  .
.
Варіант 35.  . Варіант 36.
. Варіант 36.  .
.
Варіант 37.  . Варіант 38.
. Варіант 38.  .
.
Варіант 39.  . Варіант 40.
. Варіант 40.  .
.
Варіант 41.  . Варіант 42.
. Варіант 42.  .
.
Варіант 43.  . Варіант 44.
. Варіант 44.  .
.
Питання до захисту практичної роботи:
1. В чому суть задачі підбору параметра?
2. Які способи знаходження коренів рівняння?
3. Які є основні методи відокремлення коренів?
4. Назвіть основні кроки розв'язання рівняння при відокремленні коренів табличним методом.
Державна служба України з надзвичайних ситуацій
ЧЕРКАСЬКИЙ ІНСТИТУТ ПОЖЕЖНОЇ БЕЗПЕКИ ІМЕНІ ГЕРОЇВ ЧОРНОБИЛЯ
Кафедра вищої математики та інформаційних технологій
ЗАТВЕРДЖУЮ
Начальник кафедри
ВМ та ІТ
к.ф-м.н., доц.,
полковник с.ц.з.
_______ І.П. Частоколенко
“___”______2014р.
Навчальна дисципліна: Інформаційне забезпечення діяльності підрозділів цивільного захисту
4-й курс (курсанти, студенти, слухачі).
МЕТОДИЧНА РОЗРОБКА
на проведення практичного заняття по темі № 1.2: «Задачі прогнозування та оптимізації»
Час: 12 годин, з них 4 години практичних занять, 8 годин самостійної роботи.
Тема 1.2: Розв’язання задач прогнозування.
Мета заняття: ознайомлення з можливостями побудови та аналізу часових рядів засобами MS Excel та придбання практичних навичок роботи в табличному процесорі Excel при розв’язанні задачі прогнозування методом найменших квадратів.
Метод проведення: практичне заняття.
Місце проведення: ауд. № 317, ауд. № 318.
Час проведення: 2 години
Матеріально-технічне забезпечення: ПК.
Методичну розробку підготував
Старший викладач ВМ та ІТ К.В. Григоренко
Викладач кафедри ВМ та ІТ А.П. Марченко
Методична розробка обговорена та схвалена на засіданні кафедри
Протокол №1 від “26” серпня 2014р.
Практичне заняття
Заняття № 1.2. Розв’язання задач прогнозування.
Мета роботи: ознайомлення з можливостями побудови та аналізу часових рядів засобами MS Excel та придбання практичних навичок роботи в табличному процесорі Excel при розв’язанні задачі прогнозування методом найменших квадратів.
Умова задачі. Для заданої таблиці, яка показує динаміку кількості виїздів пожежних підрозділів, зробити прогноз кількості виїздів на наступний рік, використовуючи метод найменших квадратів на основі емпіричних формул двох видів: лінійної залежності  і показникової залежності
і показникової залежності  :
:
Порядок застосування методу:
¨ В робочому листі Excel створити наступну форму:
| A | B | C | D | E | F | G | H | I | J | |
| Рік | ||||||||||
| Виїзди | ||||||||||
Лінійна залежність 
| ||||||||||
| a = | ||||||||||
| b = | ||||||||||
| Прогноз на | ||||||||||
| продаж = |
¨ В комірку B4 занести формулу “=ИНДЕКС(ЛИНЕЙН(B2:J2;B1:J1);1)”, яка дає значення параметра a лінійної залежності.
¨ В комірку B5 занести формулу “=ИНДЕКС(ЛИНЕЙН(B2:J2;B1:J1);2)”, яка дає значення параметра b лінійної залежності.
¨ В комірку B7 занести формулу “=B4*B6+B5”, яка дає значення прогнозу.
¨ В комірку B6 занести значення 1996, тобто значення року, на який створюється прогноз продажу.
Завдання:
1. Прослухати інструктаж з техніки безпеки при роботі на ПК.
2. Ознайомитися з методичними рекомендаціями по темі роботи.
Для заданої таблиці, яка показує динаміку кількості виїздів пожежних підрозділів, зробити прогноз кількості виїздів на наступний рік, використовуючи метод найменших квадратів на основі емпіричних формул двох видів: лінійної залежності  і показникової залежності
і показникової залежності  відповідно до свого варіанту.
відповідно до свого варіанту.
- Результати розв'язку задачі представити у вигляді звіту відповідно до прикладу оформлення результатів роботи, наведеного в методичних вказівках.
4. Розв’язати задачу прогнозування діяльності служби пожежної охорони за індивідуальним варіантом.
5. Захистити результати виконання практичного завдання у викладача.
Збірник варіантів завдання
Варіант 1.
| Рік | |||||||
| Виїзди |
Варіант 2.
| Рік | |||||||
| Виїзди |
Варіант 3.
| Рік | |||||||
| Виїзди |
Варіант 4.
| Рік | |||||||
| Виїзди |
Варіант 5.
| Рік | |||||||
| Виїзди |
Варіант 6.
| Рік | |||||||
| Виїзди |
Варіант 7.
| Рік | |||||||
| Виїзди |
Варіант 8.
| Рік | |||||||
| Виїзди |
Варіант 9.
| Рік | |||||||
| Виїзди |
Варіант 10.
| Рік | |||||||
| Виїзди |
Варіант 11.
| Рік | |||||||
| Виїзди |
Варіант 12.
| Рік | |||||||
| Виїзди |
Варіант 13.
| Рік | |||||||
| Виїзди |
Варіант 14.
| Рік | |||||||
| Виїзди |
Варіант 15.
| Рік | |||||||
| Виїзди |
Варіант 16.
| Рік | |||||||
| Виїзди |
Варіант 17.
| Рік | |||||||
| Виїзди |
Варіант 18.
| Рік | |||||||
| Виїзди |
Варіант 19.
| Рік | |||||||
| Виїзди |
Варіант 20.
| Рік | |||||||
| Виїзди |
Варіант 21.
| Рік | |||||||
| Виїзди |
Варіант 22.
| Рік | |||||||
| Виїзди |
Варіант 23.
| Рік | |||||||
| Виїзди |
Варіант 24.
| Рік | |||||||
| Виїзди |
Варіант 25.
| Рік | |||||||
| Виїзди |
Варіант 26.
| Рік | |||||||
| Виїзди |
Варіант 27.
| Рік | |||||||
| Виїзди |
Варіант 28.
| Рік | |||||||
| Виїзди |
Варіант 29.
| Рік | |||||||
| Виїзди |
Варіант 30.
| Рік | |||||||
| Виїзди |
Варіант 31.
| Рік | |||||||
| Виїзди |
Варіант 32.
| Рік | |||||||
| Виїзди |
Варіант 33.
| Рік | |||||||
| Виїзди |
Варіант 34.
| Рік | |||||||
| Виїзди |
Варіант 35.
| Рік | |||||||
| Виїзди |
Варіант 36.
| Рік | |||||||
| Виїзди |
Варіант 37.
| Рік | |||||||
| Виїзди |
Варіант 38.
| Рік | |||||||
| Виїзди |
Варіант 39.
| Рік | |||||||
| Виїзди |
Варіант 40.
| Рік | |||||||
| Виїзди |
Питання до захисту практичної роботи:
- Означення часового ряду
- Математичне формулювання часового ряду
- Наведіть типовий приклад часового ряду
- Яка основна мета вивченні часових рядів?
- Означення тренду
- На скільки частин розкладається задача виявлення тренда?
- Як визначаються найкращі числові значення параметрів вибраної емпіричної формули?
- Означення емпіричної формули
- Математичне представлення емпіричної формули
Державна служба України з надзвичайних ситуацій
Академія пожежної безпеки ім. Героїв Чорнобиля
Кафедра вищої математики та інформаційних технологій
ЗАТВЕРДЖУЮ
Начальник кафедри
ВМ та ІТ
к.ф-м.н., доц.,
полковник с.ц.з.
_______ І.П. Частоколенко
“___”______2013р.
Навчальна дисципліна: Інформаційне забезпечення діяльності підрозділів цивільного захисту
4-й курс (стаціонар, курсанти).
МЕТОДИЧНА РОЗРОБКА
на проведення практичного заняття по темі № 1.2: «Задачі прогнозування та оптимізації»
Час: 9 годин, з них 4 години практичних занять, 5 годин самостійної роботи.
Тема 1.3: Розв’язання задач лінійного програмування.
Мета заняття: ознайомлення з можливостями розв’язання задач лінійного програмування засобами MS Excel та придбання практичних навичок роботи в табличному процесорі Excel при розв’язанні таких задач.
Метод проведення: практичне заняття.
Місце проведення: ауд. № 317, ауд. № 318.
Час проведення: 2 години
Матеріально-технічне забезпечення: ПК.
Методичну розробку підготував
Викладач кафедри ВМ та ІТ А.П. Марченко
Методична розробка обговорена та схвалена на засіданні кафедри
Протокол №____від “__”________2013р.
Практичне заняття
Заняття № 1.3. Розв’язання задач лінійного програмування.
Мета роботи: ознайомлення з можливостями розв’язання задач лінійного програмування засобами MS Excel та придбання практичних навичок роботи в табличному процесорі Excel при розв’язанні таких задач.
Умова задачі. Знайти максимальне значення лінійної функції  за таких умов:
за таких умов:
 ,
,
 ,
,  ,
,  – цілочисельні.
– цілочисельні.
Порядок розв’язування задачі лінійного програмування:
¨ Установити надбудову Поиск решения. Для цього виконати команду Сервис-Надстройки.... Внаслідок цього з’являється вікно Надстройки. В цьому вікні у прокручуваному списку Список надстроек: слід установити прапорець на пункті Поиск решения і натиснути кнопку OK.
¨ В робочому листі Excel створити наступну форму:
| A | B | |
| Змінні: | ||
| x1 = | ||
| x2 = | ||
| Максимальне значення: | ||
| Обмеження: | ||
| №1: | ||
| №2: | ||
| №3: |
¨ Коміркам B2 і B3 присвоїти імена _x1 і _x2.
¨ В комірки B8, B9 і B10 внести такі формули: “=_x1+2*_x2”, “=0.5*_x1+0.4*_x2”, “=_x1+4*_x2”.
¨ В комірку B5 внести формулу цільової функції: «=60*_x1+160*_x2».
¨ Звернутися до надбудови Поиск решения з метою розв’язування задачі. Для цього виконати команду Сервис-Поиск решения.... Після цього на екрані з’являється вікно Поиск решения, в яке здійснюється внесення задачі ЛП.
¨ В полі Установить целевую ячеку: надрукувати $B$5.
¨ Установити відмітку на пункті Равной: Максимальному значению.
¨ В полі Изменяя ячейки: надрукувати $B$2:$B$3.
¨ Ввести перше обмеження. Для цього натиснути кнопку Добавить. У діалоговому вікні Добавление ограничения в поле Ссылка на ячейку: ввести $B$8, в полі Ограничение: вибрати значок “<=” і надрукувати значення 130. Натиснути кнопку ОК.
¨ Аналогічно ввести друге і третє обмеження.
¨ Ввести умови невід’ємності змінних. Для цього натиснути кнопку Добавить. У діалоговому вікні Добавление ограничения в поле Ссылка на ячейку: ввести $B$2:$B$3, в полі Ограничение: вибрати значок «>=» і надрукувати значення 0. Натиснути кнопку OK.
¨ Ввести умови цілочисельності змінних. Для цього натиснути кнопку Добавить. У діалоговому вікні Добавление ограничения в поле Ссылка на ячейку: ввести $B$2:$B$3, в полі Ограничение: вибрати пункт цел. Натиснути кнопку OK.
¨ Натиснути кнопку Параметри..., установити відмітку на пункті Линейная модель і натиснути кнопку OK.
¨ Задачу ЛП повністю підготовлено. Натиснути у вікні Поиск решения кнопку Выполнить.
¨ З’являється вікно Результаты поиска решения, в якому повідомляється, що Решение найдено. Відмітити пункт Сохранить найденное решение і натиснути кнопку OK. На листі ЕТ бачимо оптимальний план.
Завдання:
1. Ознайомитися з методичними рекомендаціями по темі роботи.
2. Розв’язати задачу оптимального розподілу ресурсів методом лінійного програмування для наступної цільової функції та системи ресурсних обмежень:
| Лінійна функція: | 
|
| Обмеження: | 
|
3. Результати розв'язку задачі представити у вигляді звіту відповідно до прикладу оформлення результатів роботи, наведеного в методичних вказівках.
4. Розв’язати задачу оптимального розподілу ресурсів служби пожежної охорони за індивідуальним варіантом по номеру у журналі.
5. Захистити результати виконання практичного завдання у викладача.
Збірник варіантів завдання
Не нашли, что искали? Воспользуйтесь поиском: