
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Линейные пространства
ЛИНЕЙНАЯ АЛГЕБРА
Аналитическая геометрия
1. Кривые второго порядка. Канонические уравнения кривых.
2. Поверхности второго порядка. Канонические уравнения поверхностей.
3. Цилиндрические поверхности.
Линейные пространства
1. Линейные пространства, примеры (
2. Линейно зависимые и линейно независимые элементы, их свойства.
3. Доказать: если элементы {  } являются линейными комбинациями элементов {
} являются линейными комбинациями элементов {  } и m>n, то эти элементы {
} и m>n, то эти элементы {  } являются линейно зависимыми.
} являются линейно зависимыми.
4. Дать определение n-мерного линейного пространства и его базиса. Доказать, что любой элемент линейного пространства может быть представлен в виде линейной комбинации его базисных элементов.
5. Доказать, что n элементов линейного пространства образуют его базис, если они линейно независимы и любой элемент линейного пространства может быть представлен в виде их линейной комбинации.
6. Найти базис и размерность арифметического пространства  и пространства многочленов степени меньшей или равной n.
и пространства многочленов степени меньшей или равной n.
7. Дать определение полной системы элементов n-мерного линейного пространства и показать, что она содержит не менее n элементов. Показать, что если к базису линейного пространства добавить один или несколько любых его элементов, то полученная система элементов будет полной.
8. ----- Дать определение подпространства линейного пространства Е и показать, что оно также является линейным пространством, размерность которого не превосходит размерности пространства Е.
9. Показать, что многочлены, степень которых не превосходит n, образуют подпространство линейного пространства C [ a,b ]..
10. Показать, что базис подпространства линейного пространства всегда можно дополнить некоторыми элементами до базиса всего пространства.
11. Дать определение линейной оболочки элементов {  } линейного пространства. Показать, что линейная оболочка является подпространством, а элементы {
} линейного пространства. Показать, что линейная оболочка является подпространством, а элементы {  } образуют в нем полную систему. Пояснить также, почему для линейной оболочки остаются в силе все понятия, имеющие отношение к линейным пространствам (размерность, базис, полная система).
} образуют в нем полную систему. Пояснить также, почему для линейной оболочки остаются в силе все понятия, имеющие отношение к линейным пространствам (размерность, базис, полная система).
12. Доказать, что размерность линейной оболочки элементов {  } равна максимальному числу линейно независимых элементов в системе элементов {
} равна максимальному числу линейно независимых элементов в системе элементов {  }.
}.
13. Показать, что если  - базис линейной оболочки
- базис линейной оболочки 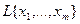 элементов
элементов  , то
, то  .
.
14. Дать определение суммы и пересечения подпространств и показать, что они сами являются подпространствами. Дать определение прямой суммы подпространств и найти ее размерность.
15. Показать, что любой элемент, принадлежащий прямой сумме подпространств  и
и  единственным образом представим в виде суммы элементов
единственным образом представим в виде суммы элементов 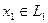 и
и  , причем, если
, причем, если  и
и  , то элементы
, то элементы  линейно независимые.
линейно независимые.
Не нашли, что искали? Воспользуйтесь поиском: