Оценка погрешности результатов косвенных измерений.

Искомая величина вычисляется по расчетной формуле.

<y>=f (<x₁>,<x₂>,…,<x _n>),

при подстановке в нее средних значений измеренных величин. Абсолютная ошибка косвенных измерений находится по обычному правилу нахождения полного дифференциала функции, в который вместо дифференциалов переменных подставляются значения полученных ошибок. При этом все знаки ²-² в формуле дифференциала заменяются на “+”. Например, косвенно измеряемая величина

y= f (x_1, x₂,…z₁ z₂…)

где x₁, x₂….. непосредственно измеряемые величины, z₁, z₂….. принятые табличные значения известных величин.

Тогда абсолютная погрешность.

Dy=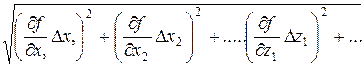

В качестве погрешностей табличных значений берется половина последней значащей цифры, однако обычно эта величина оказывается много меньше ошибок измерений и ее можно не учитывать.

Относительная погрешность определяется как отношение абсолютной погрешности к измеренной величине, как и для прямых измерений. Можно, однако, находить относительную погрешность, не определяя абсолютную.

Для этого надо.

А) прологарифмировать расчетную формулу.

y= f (x₁, x₂,… x _n);

В) Найти полный дифференциал от lny

d(lny)=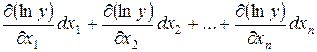

Производная от lny= 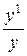, а дифференциал соответственно 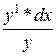представляет собой сумму относительных погрешностей по всем измеренным значениям.

Относительная погрешность косвенного измерения находится как сумма относительных погрешностей прямых измерений

=

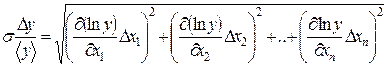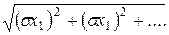
При расчете ошибок косвенных измерений, когда исходные ошибки независимы и случайны, производится их квадратичное сложение.

Окончательный результат записывается в виде

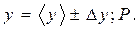
В таблице приводятся некоторые формулы для нахождения погрешностей величины, являющейся простой функцией других величин.

Таблица относительных погрешностей косвенных измерений

Не нашли, что искали? Воспользуйтесь поиском: