Закон Био-Савара-Лапласа

Основной закон электромагнетизма, закон Био-Савара-Лапласа, устанавливает соотношение между силой тока в проводнике и напряженностью магнитного поля, которое возникает в пространстве, окружающем проводник. Этот закон в СИ в векторной форме имеет вид:

(1)

где 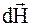– напряженность магнитного поля в точке А, созданная элементом тока на расстоянии от него,
– угол между элементом тока и радиус-вектором (рисунок 3).

Модуль вектора напряженности определяется:

. (2)

Рисунок 3 – Магнитное поле тока

По правилу векторного произведения векторов вектор 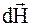направлен перпендикулярно плоскости, содержащей вектора и , векторы , и 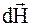образуют правую тройку.

Расчёт напряженности магнитного поля по формуле (1) в общем случае довольно сложен. Однако если распределение тока имеет определённую симметрию, то применение закона Био-Савара-Лапласа совместно с принципом суперпозиции позволяет довольно просто рассчитать конкретные поля.

Вычислим напряженность магнитного поля в центре кругового тока (в точке О, рисунок 4). По принципу суперпозиции, напряжённость магнитного поля , создаваемого всем витком, равна векторной сумме напряжённостей 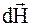, создаваемых каждым элементом тока. Как следует из правила векторного произведения векторов, все элементы кругового проводника с током создают в центре магнитное поле одного направления – вдоль нормали к плоскости витка. Поэтому сложение векторов 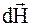можно заменить сложением их модулей 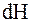. Обозначим радиус кругового тока через R. В формуле (2) для этого случая длина радиус-вектора не меняется: r = R.

Рисунок 4 – Виток с током

Угол a для всех точек окружности равен p/2, следовательно, sina = 1. На основании этого формула (2) принимает вид:

. (3)

Интегрируя это выражение по всей длине окружности, т.е. в пределах от l = 0 до l = 2pR, находим:

. (4)

Не нашли, что искали? Воспользуйтесь поиском: