Двоеженцы и четвертое измерение

В конце концов идея четвертого измерения пересекла Атлантический океан и попала в Америку. Ее вестником стала колоритная фигура — английский математик Чарльз Хауард Хинтон. Если Альберт Эйнштейн в 1905 г. корпел за письменным столом в швейцарском патентном бюро и в то же время открывал законы относительности, то Хинтон трудился в патентном бюро США в Вашингтоне, округ Колумбия. Эти двое никогда не встречались, но несколько раз их пути могли бы пересечься при довольно примечательных обстоятельствах.

Все взрослые годы своей жизни Хинтон был одержим стремлением популяризировать четвертое измерение и визуализировать его. Он хотел войти в историю науки как человек, который «видел» четвертое измерение.

Хинтон был сыном Джеймса Хинтона — известного британского отоларинголога, придерживающегося либеральных убеждений. С годами харизматичный Хинтон-старший превратился в религиозного философа, отстаивающего свободную любовь и открытую полигамию, и наконец возглавил одну влиятельную английскую секту. Его окружали беззаветно преданные ему свободомыслящие последователи. Одно из самых известных высказываний Хинтона-старшего — «Христос был Спасителем для мужчин, а я — спаситель женщин и ни капли ему не завидую!»[34]

Но его сын Чарльз, казалось, был обречен вести респектабельную и скучную жизнь математика. Его увлекало не многоженство, а многоугольники! Закончив учебу в Оксфорде в 1877 г., Чарльз стал почтенным учителем в школе Аппингема и продолжал работать над диссертацией на степень магистра математики. Еще в Оксфорде он предпринимал попытки представить себе четвертое измерение. Будучи математиком, он понимал, что представить себе четырехмерный объект во всей его целостности невозможно. Зато возможно, рассудил он, вообразить поперечное сечение или развертку четырехмерного объекта.

Свои мысли Хинтон излагал в статьях и публиковал в популярной прессе. Его авторитетная статья «Что такое четвертое измерение?» для Dublin University Magazine и Cheltenham Ladies’ College Magazine была в 1884 г. переиздана с броским подзаголовком «Призракам дано объяснение».

Однако жизнь Хинтона, до той поры небогатая событиями, вдруг совершила резкий поворот к худшему: в 1885 г. его арестовали за двоеженство и отдали под суд. До того Хинтон женился на Мэри Эверест-Буль, дочери одного из приятелей его отца и вдове великого математика Джорджа Буля, основателя булевой алгебры. Вместе с тем Хинтон был отцом близнецов, родившихся у некой Мод Уэлдон.

Директор аппингемской школы, встречая Хинтона в обществе жены Мэри и любовницы Мод, полагал, что Мод — сестра Хинтона. Для Хинтона все складывалось прекрасно — до тех пор, пока он не совершил ошибку и не женился и на Мод. Как только руководство школы узнало о двоеженстве Хинтона, вспыхнул скандал. Хинтона сразу же уволили из аппингемской школы и отдали под суд. Три дня он провел в тюрьме, но Мэри Хинтон отказалась поддержать обвинение и вскоре вместе с мужем уехала из Англии в США.

Хинтон получил место ассистента на кафедре математики Принстонского университета, где его одержимость четвертым измерением временно потеснило увлечение изобретательством: в частности, конструирование тренажера для бейсбола. Бейсбольной команде Принстона изобретение Хинтона принесло немалую пользу, так как эта машина могла подавать бейсбольные мячи со скоростью 70 миль в час (около 112 км/ч). Автоматы, сконструированные по образу машины Хинтона, теперь можно увидеть на всех крупных бейсбольных стадионах мира.

Когда же Хинтона уволили и из Принстона, его бывший начальник, ревностный сторонник теории четвертого измерения, сумел подыскать ему должность в Военно-морской обсерватории США. Затем, в 1902 г., Хинтон перешел на работу в вашингтонское патентное бюро.

Кубы Хинтона

В течение нескольких лет Хинтон разрабатывал оригинальные методы, с помощью которых не только профессиональные математики, но и любой среднестатистический человек из числа растущих рядов его последователей мог бы «увидеть» четырехмерные объекты. Наконец Хинтон усовершенствовал специальные кубы, которые при условии приложения достаточных стараний помогали визуализировать гиперкубы, или кубы в четырех измерениях. Они получили название «кубы Хинтона». Хинтон даже ввел в обращение официальное название развертки гиперкуба — тессеракт, которое прижилось в английском языке.

Кубы Хинтона широко рекламировались в женских журналах и даже применялись на спиритических сеансах, где вскоре приобрели мистическое значение. Представители высшего общества утверждали: медитируя на кубах Хинтона, можно уловить проблески четвертого измерения, а значит, и потустороннего мира духов и умерших близких. Его ученики часами изучали эти кубы, медитировали на них, пока не приобретали умение мысленно переставлять и разбирать эти кубы посредством четвертого измерения, получая гиперкуб. Высказывалось утверждение, будто бы тот, кто справляется с этой умственной задачей, способен достичь высшего состояния — нирваны.

В качестве аналогии рассмотрим трехмерный куб. Хотя флатландец не в состоянии вообразить себе этот куб целиком, мы можем представить развертку куба в трех измерениях, в итоге получим шесть квадратов, образующих крест. Разумеется, флатландец не может снова собрать из этих квадратов куб. В мире двух измерений квадраты жестко соединены между собой и лишены подвижности. А в третьем измерении стыки подвижны. Флатландец, наблюдающий это явление, увидит, как квадраты исчезают, пока в его вселенной не останется лишь один из них (рис. 3.6).

Рис. 3.6. Флатландцы не могут увидеть куб, но могут представить трехмерный куб по его развертке. С точки зрения флатландца, развернутый куб напоминает крест из шести квадратов. Мы тоже не можем увидеть четырехмерный гиперкуб, но его развертка представляет собой ряд кубов, расположенных крестообразным тессерактом. Хотя кубы тессеракта выглядят лишенными подвижности, житель четырехмерного пространства способен вновь «сложить» из кубов гиперкуб.

Точно так же нельзя представить себе гиперкуб в четырех измерениях. Но можно сделать развертку гиперкуба, разложить его на элементы — обычные для трехмерного пространства кубы. Эти кубы, в свою очередь, можно расположить трехмерным крестом — тессерактом. Мы не в силах представить себе, как сложить из этих кубов гиперкуб. А гость из высшего измерения перенесет каждый куб из нашего мира в свой и соберет из них гиперкуб. (Наблюдая за этим удивительным событием своими трехмерными глазами, мы увидим только, что другие кубы исчезают, а в нашем мире остается лишь один куб.) Влияние Хинтона распространилось настолько широко, что Сальвадор Дали воспользовался тессерактом в знаменитой картине «Распятие, или Гиперкубическое тело» из коллекции Метрополитен-музея в Нью-Йорке. Эта картина изображает Христа, распятого на четырехмерном кресте (рис. 3.7).

Рис. 3.7. На картине «Распятие, или Гиперкубическое тело» Сальвадор Дали изобразил Христа распятым на тессеракте — развернутом гиперкубе (Метрополитен-музей, дар Честера Дейла, собрание музея, 1995 г.) (1993. Ars, New York/Demart Pro Arte, Geneva).

Хинтон знал и второй способ визуализации многомерных объектов: с помощью теней, которые они отбрасывают в нижних измерениях. К примеру, флатландец может представить себе куб, посмотрев на его двумерную тень. Куб выглядит как два квадрата, соединенных вместе. Так и гиперкуб отбрасывает в третьем измерении тень, превращаясь в куб внутри куба (рис. 3.8).

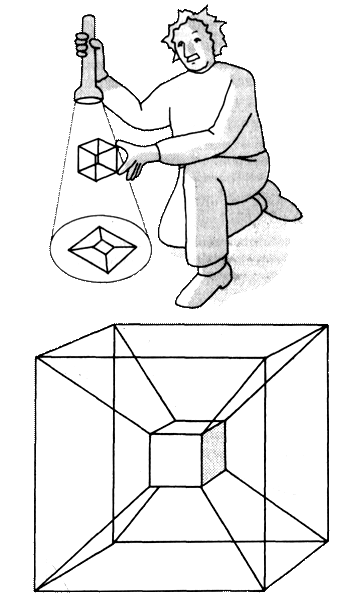
Рис. 3.8. Флатландец может визуализировать куб, изучая тень, которую он отбрасывает: эта тень выглядит как квадрат в квадрате. Если куб вращается, эти квадраты совершают движения, невозможные с точки зрения флатландца. Так и тень гиперкуба — куб внутри куба. Если гиперкуб вращается в четырехмерном пространстве, эти кубы совершают движения, немыслимые для нашего трехмерного мозга.

Помимо визуализации разверток гиперкубов и рассматривания их теней, Хинтон знал третий способ, помогающий представить четвертое измерение: способ поперечных сечений. К примеру, когда мистера Квадрата переносят в третье измерение, его глаза видят только двумерные поперечные сечения объемных предметов. Так, он видит, как круги появляются, увеличиваются в размерах, меняют цвет, а затем вдруг исчезают. Двигаясь мимо яблока, мистер Квадрат увидел бы, как красный круг возник словно из воздуха, постепенно увеличился, потом начал сжиматься, превратился в маленький коричневый кружочек (хвостик яблока) и наконец исчез. Хинтон понимал, что мы, попав в четвертое измерение, тоже могли увидеть, как странные предметы вдруг появляются откуда ни возьмись, увеличиваются, меняют цвет и форму, уменьшаются и наконец исчезают.

Итак, вкладом Хинтона можно признать популяризацию многомерных фигур с применением трех методов: изучения их теней, их поперечных сечений и их разверток. Даже сегодня к этим трем методам профессиональные математики и физики обращаются в первую очередь, когда им требуется представить многомерные объекты. Ученые, чьи схемы появляются в нынешних научных журналах, многим обязаны трудам Хинтона.

Не нашли, что искали? Воспользуйтесь поиском: