Опыт показывает, что сила , действующая на точечный заряд q, зависит в общем случае не только от положения этого заряда, но и от его скорости . Соответственно этому силу разделяют на две составляющие — электрическую (она не зависит от движения заряда) и магнитную (она зависит от скорости заряда). В любой точке пространства направление и модуль магнитной силы зависят от скорости заряда, причем эта сила всегда перпендикулярна вектору ; кроме того, в любом месте магнитная сила перпендикулярна определенному в данном месте направлению и, наконец, ее модуль пропорционален той составляющей скорости, которая перпендикулярна этому выделенному направлению.

Все эти свойства магнитной силы можно описать, если ввести понятие магнитного поля. Характеризуя это поле вектором 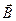, определяющим выделенное в каждой точке пространства направление, запишем выражение для магнитной силы в виде

(1)

Тогда полная электромагнитная сила, действующая на заряд q:

(2)

Ее называют силой Лоренца. Последнее выражение является универсальным: оно справедливо как для постоянных, так и для переменных электрических и магнитных полей, причем при любых значениях скорости заряда.

По действию силы Лоренца на заряд можно в принципе определить модули и направления векторов и 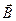. Поэтому выражение для силы Лоренца можно рассматривать как определение электрического и магнитного полей (в случае электрического поля мы так и поступили).

Следует подчеркнуть, что на покоящийся электрический заряд магнитное поле не действует. В этом существенное отличие магнитного поля от электрического. Магнитное поле действует только на движущийся заряд.

Вектор 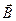характеризует силовое действие магнитного поля на движущийся заряд и, следовательно, является в этом отношении аналогом вектора , характеризующего силовое действие электрического поля.

Важной особенностью магнитной силы является то, что она всегда перпендикулярна вектору скорости заряда, поэтому работы над зарядом не совершает. Это значит, что в постоянном магнитном поле энергия движущейся заряженной частицы всегда остается неизменной, как бы частица ни двигалась.

В нерелятивистском приближении сила Лоренца (2), как и любая другая сила, не зависит от выбора системы отсчета (инерциальной). Вместе с тем магнитная составляющая силы Лоренца меняется при переходе от одной системы отсчета к другой (из-за ). Поэтому должна меняться и электрическая составляющая . Отсюда следует, что разделение полной силы — силы Лоренца — на электрическую и магнитную зависит от выбора системы отсчета. Без указания системы отсчета такое разделение не имеет смысла.

Магнитное поле равномерно движущегося заряда. Опыт показывает, что само магнитное поле порождается движущимися зарядами (токами). В результате обобщения экспериментальных данных был получен элементарный закон, определяющий поле 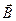точечного заряда q, движущегося с постоянной нерелятивистской скоростью . Этот закон записывается в виде

(3)

где - магнитная постоянная; коэффициент

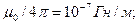
-радиус-вектор, проведенный от заряда q к точке наблюдения.. Отметим, что вектор 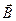является аксиальным (псевдовектором).

Величину 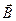называют магнитной индукцией.

Единицей магнитной индукции служит тесла (Тл).

Электрическое поле точечного заряда q, движущегося с нерелятивистской скоростью, описывается аналогичным законом. Поэтому выражение (3) можно представить как

(4)

где с — электродинамическая постоянная (), она равна скорости света в вакууме к электрической силе становится сравнимой с последней (заметим, что это отношение справедливо и при релятивистских скоростях).

Принцип суперпозиции. Опыт дает, что для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитное поле, создаваемое несколькими движущимися зарядами или токами, равно векторной сумме магнитных полей, создаваемых каждым зарядом или током в отдельности:

(6)

Закон Био-Савара. Рассмотрим вопрос о нахождении магнитного поля, создаваемого постоянными электрическими токами, исходя из закона (3), определяющего индукцию поля В равномерно движущегося точечного заряда. Подставим в (3) вместо q заряд , где dV — элементарный объем, ρ — объемная плотность заряда, являющегося носителем тока, и учтем, что = j Тогда формула (3) приобретет следующий вид:

(7)

Если же ток I течет по тонкому проводу с площадью поперечного сечения то

где элемент длины провода. Введя вектор dl в направлении тока I, перепишем предыдущее равенство так:

(8)

Векторы jdV и Idl называют соответственно объемным и линейным элементами, тока. Произведя в формуле (7) замену объемного элемента тока на линейный, получим

(9)

Формулы (7) и (9) выражают закон Био-Савара..

Полное поле 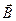в соответствии с принципов суперпозиции определяется в результате интегрирования выражений (7) или (9) по всем элементам тока:

(10)

Расчет по этим формулам индукции магнитного поля тока произвольной конфигурации, вообще говоря, сложен. Однако расчет значительно упрощается, если распределение тока имеет определенную симметрию

МЕТОДИКА ИЗМЕРЕНИЙ

Получим выражение для расчёта индукции магнитного поля на оси

кругового тока (рис.1).

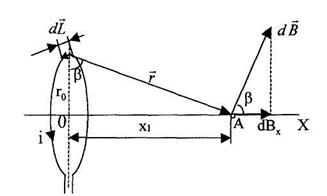
Рис.1

Из закона Био – Савара - Лапласа индукция магнитного поля от элемента кругового тока

в точке А равна

или в скалярной форме

, (11)

так как угол между векторами и равен .

Осевая составляющая индукции магнитного поля от элемента тока

. (12)

Индукция от кругового витка с током направлена вдоль оси витка ОХ и согласно

(11) запишется

. (13)

Учитывая, что

, (14)

получим

, (15)

где - расстояние от центра витка до рассматриваемой точки А.

Теперь рассмотрим соленоид, как систему круговых токов, соединенных последовательно. Определим индукцию магнитного поля в произвольной точке О на оси соленоида (рис.2).

Рис.2

Пусть на единицу длины соленоида приходится n витков. Тогда на участке dx будет

(ndx) витков, которые в точке О создадут магнитное поле и индукцией

. (16)

Из геометрических построений, показанных на рис.2,следует

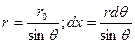(17)

Подставляя (17) в (16), имеем

. (18)

Интегрируя (18), получаем выражение для расчета индукции магнитного поля на оси

соленоида

(19)

где и - углы между радиусами-векторами, проведенными из точки О к крайним виткам, и осью соленоида.

Приблизительный вид изменения индукции магнитного поля вдоль оси соленоида показан на рис.3. Значение x =0

соответствует средней точке на оси соленоида.

Получим формулу для расчёта индукции

магнитного поля в средней точке на оси

соленоида длиной L и диаметром D.В этом

случае

Рис.3

Учитывая, что (где N – число витков в соленоиде), из (9) для средней точки на оси соленоида имеем

(20)

В случае бесконечно длинного соленоида , тогда из (19) получаем

(21)

В работе для изучения индукции магнитного поля на оси соленоида используется метод, основанный на явлении(эффекте) Холла.

Это возникновение в твердом проводнике (или полупроводнике) с током плотностью ,помещенном в магнитное поле с индукцией 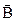, электрического поля напряженностью .Как следствие, между электродами, касающимися боковых граней образца, возникнет разность потенциалов (см.рис.4)

ЭДС Холла может быть записана в виде

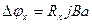(22)

где 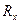- постоянная Холла, а – ширина проводника.

Плотность тока определяется формулой

, (23)

где 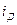- управляющий ток через датчик Холла.

Подставляя (23) в (22), получаем

. (24)

Обычно значение постоянной Холла для полупроводников значительно больше, чем для проводников.

⇐ Предыдущая 123 Следующая ⇒

Не нашли, что искали? Воспользуйтесь поиском: