
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Равновесие сочлененных систем тел
Сочлененной системой тел называется совокупность тел соединенных между собой, с помощью связей или просто соприкасающихся друг с другом.
Статический расчет инженерных сооружений во многих случаях сводится к рассмотрению условий равновесия конструкции из системы сочлененных тел, соединенных связями. Связи, соединяющие части данной конструкции, будем называть внутренними, в отличие от внешних связей, скрепляющих конструкцию с телами, в неё не входящими.
Для арки, показанной на рис. 1.15, количество неизвестных реакций (4) больше количества независимых уравнений равновесия (3). Для решения задачи необходимо дополнительно рассмотреть равновесие одной или нескольких частей конструкции.

Рис. 1.15
Составляя уравнения равновесия сил, действующих на арку, получим три уравнения с четырьмя неизвестными ХА, YА, ХВ, YВ. Рассмотрев дополнительно условия равновесия левой (или правой) ее части, получим еще три уравнения, содержащие два новых неизвестных ХC, YC (рис. 1.16). Решая полученную систему шести уравнений, найдем все шесть неизвестных.

Рис. 1.16
Другой вариант решения подобных задач состоит в том, что конструкцию расчленяют на отдельные тела и составляют уравнения равновесия каждого из тел в отдельности. При этом реакции внутренних связей будут попарно равны по модулю и противоположны по направлению. Для конструкции из п тел, на каждое из которых действует произвольная плоская система сил, получится 3 n независимых уравнений, позволяющих найти 3 n неизвестных.
 Задача
Задача
Вес однородной арки 1 равен 100 Н. Пренебрегая весом балки 2, определить максимальную интенсивность q max распределенной нагрузки, для того чтобы момент в заделке А равнялся 70 Н∙м, если арка 1 имеет форму полуокружности и размеры ВС = 3∙ АС = 0,5 м.
________________________________________________________
Решение:
 Для решения задачи сначала рассмотрим равновесие арки 1, а затем балки 2.
Для решения задачи сначала рассмотрим равновесие арки 1, а затем балки 2.
Применим принцип освобождаемости от связей и заменим связи соответствующими реакциями.
Для арки составим уравнение равновесия:  и найдем вертикальную составляющую реакции в шарнире В.
и найдем вертикальную составляющую реакции в шарнире В.


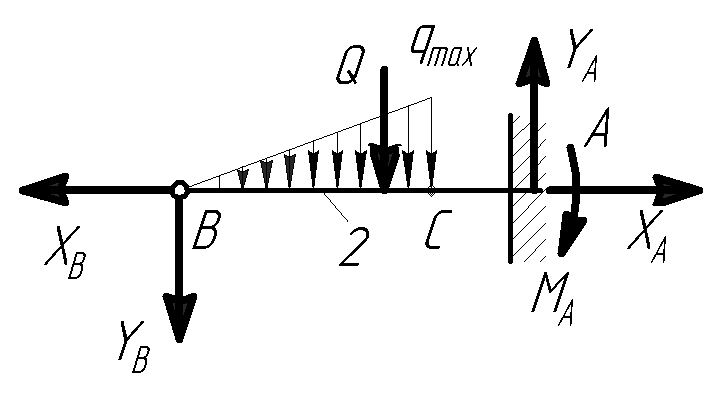 Для балки составим уравнение моментов относительно точки А:
Для балки составим уравнение моментов относительно точки А:  .
.


Подставляя числовые значения получим  Н/м.
Н/м.
Ответ: q max = 441,8 Н/м.
Не нашли, что искали? Воспользуйтесь поиском: