
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Задание вектора в пространстве.
Любой вектор в пространстве имеет длину и направление.
Длина вектора │ а │=  .
.
Направление вектора задают три направляющих косинуса: cos α, cos β, cos γ, где Ðα- угол между 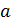 и ОХ, Ðβ- угол между a и ОУ, Ðγ- угол между a и OZ.
и ОХ, Ðβ- угол между a и ОУ, Ðγ- угол между a и OZ.
| i |
| β |
| y |
| O |
| х |
| j |
| γ |
| k |
| z |
| α |
Ðα= Ð (a,i), Ðβ=Ð (a,j), Ðγ =Ð (a,k).
cos α=  , cos β=
, cos β=  , cos γ=
, cos γ=  .
.
Свойство направляющих косинусов:
cos2 α+ cos2 β+ cos2 γ= 1.
Определение: Единичный вектор, имеющий своими координатами направляющие косинусы вектора a называется единичным вектором направления а и обозначается a 0= (cosα, cosβ, cosγ).
| а |
| а0 |
Не нашли, что искали? Воспользуйтесь поиском: