Предварительные теоретические сведения.

Численное решение задачи об устойчивости сжатого стержня

Задание.

Используя метод конечных разностей, определить минимальное собственное значение оператора краевой задачи /минимальную критическую силу, сжимающую стержень/ (требуется составить программу в системе MATLAB (на M-языке) и выполнить ручной счет):

(2.1)

Варианты задания.

– жесткость балки;

– длина балки; – номер группы; – номер студента по журналу.

Принять для расчета на ЭВМ число точек .

Предварительные теоретические сведения.

Решение задачи состоит в составлении системы конечно-разностных уравнений при разбиении отрезк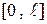а на частей с постоянным шагом и нумерацией точек разбиения : . Вводим обозначения: – координата -ой точки разбиения, . Тогда, заменяя в задаче (2.1) для каждой точки разбиения дифференциальное уравнение соответствующим разностным и учитывая нулевые граничные условия, а также умножая каждое -е уравнение на , получим алгебраическую обобщенную задачу на собственные значения -го порядка:

(2.2)

Перепишем (2.2) в векторно-матричном виде:

, (2.3)

где

; ; (.2.4)

; . (2.5)

Не нашли, что искали? Воспользуйтесь поиском: