ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Свойства криволинейного интеграла первого рода
Криволинейный интеграл I рода обладает следующими свойствами:
1. Интеграл не зависит от ориентации кривой;
2. Пусть кривая C 1 начинается в точке A и заканчивается в точке B, а кривая C 2 начинается в точке B и заканчивается в точке D (рисунок 2). Тогда их объединением будет называться кривая C 1 U C 2, которая проходит от A к B вдоль кривой C 1 и затем от B к D вдоль кривой C 2. Для криволинейных интегралов первого рода справедливо соотношение
3. Если гладкая кривая C задана параметрически соотношением 
и скалярная функция F непрерывна на кривой C, то
4. Если C является гладкой кривой в плоскости O xy, заданной уравнением 
, то
5. Если гладкая кривая C в плоскости O xy определена уравнением 
, то
6. В полярных координатах интеграл 
выражается формулой
где кривая C задана в полярных координатах функцией 
.
вдоль отрезка прямой y = x от начала координат до точки (2,2) (рисунок 3).
Решение.
| 
| |
| Рис.3 | Рис.4 |
, где C − дуга окружности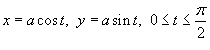 
.
Решение.
Запишем дифференциал дуги кривой:
Тогда, применяя формулу
в плоскости O xy, получаем
, где переменная s − длина дуги кривой. Тогда производная векторной функции
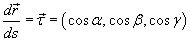представляет собой единичный вектор, направленный вдоль касательной к данной кривой (рисунок 1). В приведенной выше формуле α, β и γ − углы между касательной и положительными направлениями осейOx, Oy и Oz, соответственно.
| 
| |
| Рис.1 | Рис.2 |
Введем векторную функцию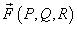 
, определенную на кривой C, так, чтобы для скалярной функции
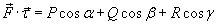
существовал криволинейный интеграл 
. Такой интеграл называется криволинейным интегралом второго рода от векторной функции 
вдоль кривой C и обозначается как
Таким образом, по определению,
где 
− единичный вектор касательной к кривой C.
Последнюю формулу можно переписать также в векторной форме:
где 
.
Если кривая C лежит в плоскости Oxy, то полагая R = 0, получаем
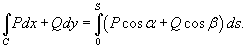
Свойства криволинейного интеграла второго рода
Криволинейный интеграл II рода обладает следующими свойствами:
1. Пусть C обозначает кривую с началом в точке A и конечной точкой B. Обозначим через −Cкривую противоположного направления - от B к A. Тогда
2. Если C − объединение кривых C1 и C2 (рисунок 2 выше), то
3. Если кривая C задана параметрически в виде 
, то
4. Если кривая C лежит в плоскости Oxy и задана уравнением 
(предполагается, что R =0и t = x), то последняя формула записывается в виде
, где кривая C задана параметрически в виде 
.
Решение.
Используя формулу
находим ответ:
с непрерывными частными производными первого порядка 
. Тогда справедлива формула Грина
где символ 
указывает, что кривая (контур) C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки. Если 
, то формула Грина принимает вид
где S − это площадь области R, ограниченной контуром C. Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля. Пусть векторное поле описывается функцией
Ротором или вихрем векторного поля 
называется вектор, обозначаемый 
или 
и равный
Формула Грина в векторной форме записывается в виде
Заметим, что формула Грина вытекает из "теоремы Стокса" при переходе от трехмерного случая к случаю двух координат.
, где кривая C − окружность радиуса R.
Решение.
Запишем компоненты векторного поля:
С помощью формулы Грина
преобразуем криволинейный интеграл в двойной:
Переходя к полярным координатам, находим искомый интеграл:
не зависит от пути интегрирования, если P, Q и R являются непрерывными функциями в области интегрирования D и в этой области существует скалярная функция 
, такая, что
В этом случае криволинейный интеграл второго рода от функции вдоль кривой C от точки A до точки Bвыражается формулой
(Здесь можно увидеть аналогию с формулой Ньютона-Лейбница для определенных интегралов.) Таким образом, если криволинейный интеграл не зависит от пути интегрирования, то для любого замкнутого контура C справедливо соотношение
Векторное поле, обладающее свойством 
, называется потенциальным, а функция называется потенциалом.
Признак потенциальности поля
Криволинейный интеграл II рода от функции не зависит от пути интегрирования, если
Предполагается, что каждый компонент функции имеет непрерывные частные производные по переменным x, y и z. Если криволинейный интеграл рассматривается в плоскости Oxy, то в случае потенциального поля будет справедливо соотношение
В этом случае признак потенциальности векторного поля упрощается и принимает вид
Рассмотренный признак является необходимым, но, вообще говоря, не достаточным для потенциальности поля. Данное условие достаточно, если только область интегрирования D односвязна.