
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
По дисциплине «Термодинамика, теплопередача и гидравлика» слушатели-заочники должны выполнить одну контрольную работу. Задание на контрольную работу состоит из 100 вариантов. Две последние цифры номера шифра слушателя-заочника определяют вариант задания на контрольную работу (табл. 1). Например, 13/24. Вариант задания 24. По таблице 1 определяем номера задач: 8, 16, 35, 57(в), 62(а), 91(б), 99(г). Работа должна быть выполнена разборчивым подчерком, грамотно и аккуратно оформлена. В тетради необходимо оставлять поля. Работы, выполненные не по своему варианту, рассматриваться не будут. При выполнении контрольных работ необходимо:
− выписать условие задачи;
− решение сопровождать краткими пояснениями, в которых показать, какая величина определяется и по какой формуле, какие величины подставляются в формулу и откуда они берутся (например, из условия задачи, из справочника, определены ранее);
− проставить размерности (в системе СИ (SI – system international));
− задачи сопровождать соответствующими схемами или диаграммами;
− сформулировать краткие выводы по результатам расчетов.
Выполненные задания должны быть своевременно сданы на проверку. Слушатели-заочники, не представившие в срок на проверку контрольную работу без уважительной причины, на экзаменационную сессию не вызываются.
Контрольная работа принимается, если она не содержит ошибок принципиального характера, и защищается при личной беседе с преподавателем. Если работа выполнена неверно, она возвращается с указаниями для исправления. Не разрешается вносить исправления в первоначальный текст. Новое решение прилагается к выполненному ранее.
Правила оформления титульного листа контрольной работы приводится в приложении 15 настоящего пособия.
Примеры решения задач
Пример 1. К двум точкам горизонтального трубопровода присоединен U -образный стеклянный дифманометр, заполненный ртутью (рис. 1). Разность уровней ртути в дифманометре h =26 мм. какова разность давлений в этих точках, если по трубопроводу проходит вода?

Рисунок 1 - U-образный стеклянный дифманометр
Решение: Из условия равенства давлений на уровне а-а слева и справа

находим, заменяя  через
через 
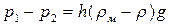
где  - плотность жидкости в трубопроводе,
- плотность жидкости в трубопроводе,  - плотность жидкости в дифманометре.
- плотность жидкости в дифманометре.
По условию задачи h =0,026 м,  =13600 кг/м3
=13600 кг/м3
Для воды  =1000 кг/м3
=1000 кг/м3

Пример 2. Определить кинематическую вязкость воды при температуре 17 ˚С.
Решение: По справочным данным вязкость воды при 10 ˚С и 20 ˚С соответственно равна 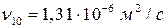 и
и 
Для определения искомой величины используем метод линейной интерполяции по следующей формуле:
 ;
;
 .
.
Пример 3. По трубе постоянного сечения из открытого резервуара (рис. 2) вода вытекает в атмосферу под постоянным напором H. На середине трубы длиной L и диаметром d установлен кран K. Определить скорость и расход вытекающей воды. Построить напорную и пьезометрическую линии. При определении потерь напора принять коэффициенты трения λ = 0,04; входа ξ вх = 0,5; крана ξ кр = 5.
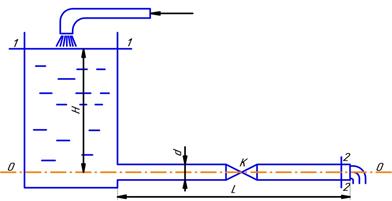
Рисунок 2 – Истечение из резервуара по длинной трубе
Решение: Для решения задачи воспользуемся уравнением Бернулли, записанном для сечений 1-1 и 2-2, проведённых по уровню жидкости в резервуаре и на выходе жидкости из трубы
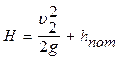 ,
,  ;
;
где 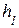 - потери по длине, м;
- потери по длине, м;  - потери в местных сопротивлениях, м.
- потери в местных сопротивлениях, м.
Потери по длине определяют по формуле Дарси – Вейсбаха  , а в местных сопротивления – по формуле Вейсбаха
, а в местных сопротивления – по формуле Вейсбаха  . Тогда
. Тогда  , откуда
, откуда

Расход вытекающей из трубы жидкости определим по уравнению расхода
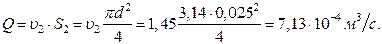
Пьезометрическая линия выражает собой характер изменения удельной потенциальной энергии (положения и состояния) в каждом сечении потока жидкости в трубе (от входа до выхода из неё).
Напорная линия выражает собой характер изменения удельной механической энергии (потенциальной и кинетической) в каждом сечении потока жидкости в трубе (от входа до выхода из неё).
Для построения напорной линии определим потери напора на различных участках трубопровода:
в сечении  (на входе в трубу) -
(на входе в трубу) -
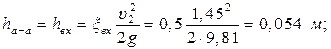
в сечении  (потери на входе в трубу и на половине трубы до крана) –
(потери на входе в трубу и на половине трубы до крана) –

в сечении  (потери на входе в трубу, на половине трубы и в кране) –
(потери на входе в трубу, на половине трубы и в кране) –

в сечении  (потери на входе в трубу, на половине трубы, в кране и на второй половине трубы) –
(потери на входе в трубу, на половине трубы, в кране и на второй половине трубы) –

По уровню жидкости в резервуаре проводим напорную плоскость, определяющую первоначальный запас энергии жидкости в резервуаре.
Откладывая от напорной плоскости в указанных сечениях соответствующие им значения потерь напора получим точки А, Б, С, Д, принадлежащие напорной линии. Соединяя эти точки, получим напорную линию.
Диаметр трубопровода не изменяется, следовательно постоянен и скоростной напор в каждом сечении трубопровода

Пьезометрическая линия пройдёт ниже напорной, параллельно ей отстоит от неё на величину скоростного напора

На рисунке 3 в масштабе выполнены построения напорной и пьезометрической линий.

Рисунок 3 – Построение напорной и пьезометрической линий
Пример 4. Определить режим течения воды температурой 15 ˚С в трубе прямоугольного сечения с размерами сторон 20´40 мм, если расход равен 1 л/с.
Решение: По справочным данным вязкость воды при 10 ˚С и 20 ˚С соответственно равна 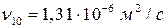 и
и 

Расход воды  .
.
Скорость движения воды 
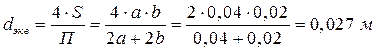
 турбулентный
турбулентный
Пример 5. Определить силу избыточного давления и центр давления на наклонную крышку, которая закрывает круглую трубу диаметром 1 м водовыпуска из пожарного водоема. Угол наклона крышки 600. Ось водовыпуска находится на глубине 2 м.

Рисунок 4 – Схема пожарного водоема
Решение: Силу давления на крышку определим аналитическим способом как произведение гидростатического давления в центре тяжести крышки на ее площадь
Р = ρ ∙ g ∙ H ∙ ω
Площадь крышки, имеющей форму эллипса
ω = πab
а и b – полуоси эллипса.
а = 0,5; b = a/sin α = 0,5/0,866 = 0,577 м.
ω = 3,14 ∙ 0,5 ∙ 0,577 = 0,906 м2.
Тогда
Р = 1000 ∙ 9,81 ∙ 2 ∙ 0,906 = 17,17 кН.
Расстояние до центра тяжести эллипса
lцт = H/sin α = 2/0,866 = 2,3 м.
Координата центра давления
lцд= lцт + I0/(lцт ∙ ω)
Момент инерции эллипса
I0 = πab3/4 = 3,14 ∙ 0,5 ∙ 0,5773/4 = 0,075 м4
Тогда
lцд = 2,3 + 0,075/(2,3 ∙ 0,906) = 2,336 м.
Задача 6. Открытая вертикально расположенная цилиндрическая емкость диаметром d = 3 м заполнена нефтью, высота столба которой Н 1 равна 2 м над отверстием в дне емкости. Определить, за какое время уровень нефти в емкости Н 2 станет равным 1 м, если коэффициент расход равен µ = 0,68, а диаметр отверстия d отв = 50 мм. Сколько понадобится времени, чтобы емкость полностью опорожнилась?
Решение. Время истечения жидкости из отверстия определяется по формуле:

где S – площадь горизонтального сечения резервуара, м2:

Н н и Н к – начальный и конечный уровень жидкости в сосуде соответственно, м;
Площадь отверстия:
 .
.
Уровень нефти в емкости понизится с 2 м и станет равным 1 м за время:

Для полного опорожнения емкости требуется время:

Пример 7. Определить высоту вертикальной сплошной струи, если вода выходит через насадок диаметром 19 мм при напоре 30 м.
Решение: высоту вертикальной сплошной струи определим по формуле Люгера:
Нв = Н/1+φН
Коэффициент φ
φ = 0,25/d + (0,1d)3 = 0,25/19+(0,1·19)3 = 9,67·10-3
Тогда
Нв = 30/1+9,67·10-3 ·30 = 23,25 м.
Пример 8. 2 м3 водяного пара при постоянном давлении 0,85 МПа нагревается от 100 до 3000С. Определить конечный объем пара, количество сообщенного тепла и работу, совершаемую паром при нагревании, принимая теплоемкость температуры нелинейной.
Решение: Переведем дано в СИ
V1 = 2 м3;
p = 0,85 МПа = 0,85.106 Па – const;
t1 =1000C, T1 = 373 K;
t2 = 3000C, T2 = 573 K.
Задача на исследование изобарного процесса.
p = const; V1/V2 = T1/T2;
Q = m.Cрm.(T2 – T1); L = p.(V2 – V1).
Из уравнения Клапейрона:
m = p.V1/(R.T1);
где R= 461,8 Дж/(кг.К) по приложению 2.
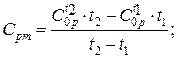
где по приложению 5:  1,8728 кДж/(кг.К);
1,8728 кДж/(кг.К);  1,9192 кДж/(кг.К).
1,9192 кДж/(кг.К).
Определим конечный объем пара:
V2 = V1.T2/T1 = 2.573/373 = 3,07 м3.
Определим массу пара
m = p.V1/(R.T1) = 0,85.106.2/(461,8.373) = 9,87 кг.
Вычислим среднюю удельную теплоёмкость пара в интервале от 100 до 300ºС:
 1,9424 кДж/(кг.К).
1,9424 кДж/(кг.К).
Определим количество теплоты, сообщенной пару:
Q = 9,87.1,9424.(573 - 373) = 3830 кДж.
Определим работу, совершаемую паром:
L = 0,85.106.(3,07 – 2) = 910000 Дж = 910 кДж;
[L] = Па.м3 = 
Вычертим график процесса (рис. 5).

Рисунок 5 – График процесса к примеру 8
Пример 9. Баллон с кислородом О2 емкостью 40 л при давлении газа 12 МПа и начальной температуре 220C оказался в зоне очага пожара. Определить, до какой температуры нагреется газ, если установлено, что он может получить 600 кДж тепла, а также каково при этом будет давление кислорода. Теплоемкость газа принять постоянной.
Решение: Переведем дано в СИ
V = 40 л = 0,04 м3;
p1 = 12 МПа = 12.10 6 Па;
t1 = 220C, T1 = 295 K;
Q = 600 кДж = 6000000 Дж.
Задача на исследование изохорного процесса, V = const.
1) Определим массу кислорода в баллоне:
m = p1.V/(R.T1);
где R = 259,8 Дж/(кг.К) по приложению 2.
m = 12.106.0,04/(259,8.295) = 6,28 кг.
2) Определим температуру кислорода в конце процесса нагревания:
Q = m.Cvm.(T2 – T1),
откуда
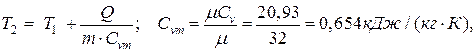
где: µ = 32 кг/кмоль; µСv = 20,93 кДж/(кмоль.К) – приложения 2 и 3, тогда

3) Определим конечное давление кислорода в баллоне:

4) Вычертим график процесса (рис. 6).
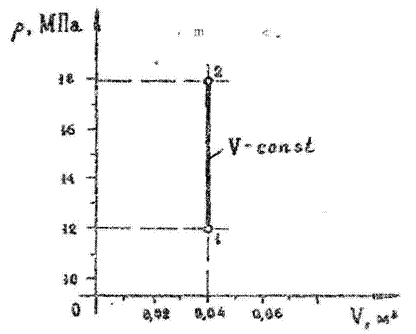
Рисунок 6 – График процесса к примеру 9
Ответ: 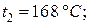
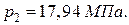
Вывод: в процессах при постоянном объеме все сообщенное количество тепла идет только на нагревание газа; при этом давление газа увеличивается прямо пропорционально изменению его абсолютной температуре: 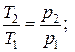
 следовательно, при организации тушения пожаров следует предусматривать мероприятия по охлаждению закрытых аппаратов, емкостей с газами и парами с целью предотвращения возможного их взрыва.
следовательно, при организации тушения пожаров следует предусматривать мероприятия по охлаждению закрытых аппаратов, емкостей с газами и парами с целью предотвращения возможного их взрыва.
Пример 10.. В теплообменнике типа «труба в трубе» нагреваемая вода температурой 40 0С движется со скоростью 1,5 м/с по кольцевому каналу. Наружный и внутренний диаметры канала равны 26 и 20 мм, длина канала – 1,4 м. Средняя температура наружной поверхности внутренней трубы равна 70 °С. Определить тепловой поток, подводимый к нагреваемой воде.
Решение. Записываем расчетное уравнению в следующем виде
 .
.
Выписываем свойства воды из приложения 1:
– при 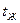 = 40 0С,
= 40 0С,  = 0,635 Вт/(м.К);
= 0,635 Вт/(м.К);  = 0,66·10-6 м2/с;
= 0,66·10-6 м2/с;  = 4,33;
= 4,33;
– при  = 70 0С,
= 70 0С,  = 2,55.
= 2,55.
Рассчитываем:
– эквивалентный диаметр кольцевого канала
 мм;
мм; 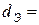 0,006 м;
0,006 м;
– числа подобия
 ;
;
 ;
;
– коэффициент теплоотдачи
 Вт/(м2.К);
Вт/(м2.К);
– линейную плотность теплового потока по формуле
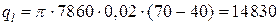 Вт/м;
Вт/м;
– тепловой поток по уравнению
 Вт.
Вт.
Пример 11. Трансформаторное масло поступает в маслоохладитель с температурой t 1 = 80 °С, а охлаждающая вода t 2 = 20 °С. Расход трансформаторного масла G 1 = 0,3 кг/ч, его теплоемкость С р1 = 1,905 кДж/(кг·К); расход воды G 2 = 0,55 кг/ч, ее теплоемкость С р2 = 4,178 кДж/(кг·К); коэффициент теплопередачи от масла к воде К = 1000 Вт/(м2·К); а передаваемый тепловой поток Q = 23 кВт. Рассчитайте площадь теплообмена маслоохладителя, если теплоносители движутся по противоточной схемам.
Решение: Используя уравнение теплового баланса, определяем температуры носителей на выходе
 ;
;

 t1=80 оС масло t3=39,8 оС
t1=80 оС масло t3=39,8 оС
 t4 =30 оС вода t2 =20 оС
t4 =30 оС вода t2 =20 оС


Поскольку отношение  >2, применяем для расчета среднего температурного напора следующую формулу:
>2, применяем для расчета среднего температурного напора следующую формулу:
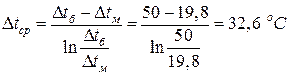 .
.
Площадь теплообмена маслоохладителя:
 .
.
Пример 12. Железобетонная плита на известняковом щебне подвергается одностороннему обогреву в условиях стандартного температурного режима. Толщина плиты 0,22 м, толщина защитного слоя арматуры 0,025 м. Начальная температура плиты равна 20 0С. Определить температуру на поверхности арматуры через 1 ч обогрева и сделать вывод о возможности обрушения конструкции, если критическая температура арматуры равна 470 0С.
Дано: железобетон на известняковом щебне; δ = 0,22 м; х = 0,025 м; t 0 = 20 °С; τ = 1 ч; t кр = 470 0С. 
Решение. По приложению 6 определим физические параметры бетона на известняковом щебне при температуре 450 °С:
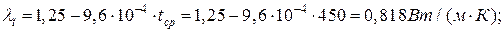

ρ = 2190 кг/м3.
Определим коэффициент температуропроводности:

Проверяем условие: 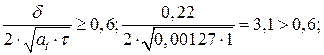 следовательно, температурное поле можно рассчитать по уравнению нестационарной теплопроводности для полуограниченного тела.
следовательно, температурное поле можно рассчитать по уравнению нестационарной теплопроводности для полуограниченного тела.
Определим величину аргумента функции Крампа для х = 0,025 м:

По приложению 13 находим значение функции Крампа: f(A) = 0,6494.
Определим температуру на поверхности арматуры через 1 ч обогрева:

Температура на поверхности арматуры плиты через 1 ч обогрева равна 451 °С. Обрушения плиты через 1 ч обогрева в условиях стандартного температурного режима не произойдет, т.к. температура на поверхности арматуры меньше критической: 451 °С < 470 °С.
Пример 13. В помещении, размеры которого 30×12×4 м, возможно горение разлитого бензина на площади 30 м2. Определить, пользуясь номограммой, среднеобъемную температуру среды при пожаре через 9 мин, принимая коэффициент избытка воздуха равным 2, а коэффициент неполноты сгорания 0,95.
Дано: l = 30 м; b = 12 м; h = 4 м; f = 30 м2; τ = 9 мин; α m = 2; η = 0,95. t f =?
Решение: По приложению 11 находим параметры, характеризующие горение бензина:
M = 160 кг/(м2.ч); 
 = 41870 кДж/кг.
= 41870 кДж/кг.
Определим площадь поверхности теплообмена в помещении:
F = 2·l·b+2·l·h+2·b·h = 2·30·12 + 2·30·4 + 2·12·4 = 1056 м2.
Определим плотность теплового потока:
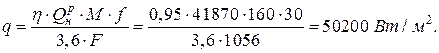
Пользуясь номограммой для определения среднеобъемной температуры среды при пожаре в помещениях [2, рис. 58, стр. 159], определяем искомую температуру в следующей последовательности:
- на левой оси ординат номограммы находим точку, соответствующую  ; параллельно линиям типа 1 с учетом визуальной интерполяции проводим прямую до пересечения с осью температур при α m = 1 и находим t = 9500C;
; параллельно линиям типа 1 с учетом визуальной интерполяции проводим прямую до пересечения с осью температур при α m = 1 и находим t = 9500C;
- затем эквидистантно кривым типа 2 (т. е. сохраняя характер кривизны с учетом визуальной интерполяции) проводим линию до пересечения с ординатой, соответствующей значению α m = 2;
- полученную точку пересечения параллельно оси абсцисс проецируем на ординату, соответствующей времени 30 мин, а затем эквидистантно линиям типа 3 опускаемся до пересечения с ординатой, соответствующей времени 9 мин;
- полученную точку пересечения проецируем параллельно оси абсцисс на ось температур и читаем ответ: t = 5200C.
Ответ: среднеобъемная температура среды в помещении при данных условиях горения бензина равна 5200С.
Пример 14. Определить излучательную способность и тепловой поток стенки площадью 6 м2, если степень ее черноты  а температура 1300
а температура 1300  .
.
Дано: F = 6 м2;  ; t = 1300ºС, T = 1573 K. E =? Ф =?
; t = 1300ºС, T = 1573 K. E =? Ф =?
Решение: Определяем излучательную способность стенки:
E =  C0 (T/100)4,
C0 (T/100)4,
здесь C0 = 5,77 Вт/(м2 К4), отсюда
E = 0,9·5,77·(1573/100)4 = 317931,2467 Вт/м2  317,93 кВт/м2.
317,93 кВт/м2.
Определяем тепловой поток стенки:
Ф = EF = 317,93·6 = 1907,58 кВт.
Ответ: E = 317,93 кВт/м2, Ф = 1907,58 кВт.
Пример 15. Определить, во сколько раз уменьшится плотность теплового потока между двумя плоскопараллельными поверхностями, степень черноты которых  если между ними установить однослойный экран из полированного алюминия.
если между ними установить однослойный экран из полированного алюминия.
Дано: 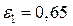 ;
;  ; Экран – полированный алюминий.
; Экран – полированный алюминий.  =?
=?
Решение: Находим приведенную степень черноты данной системы тел «поверхность 1 – поверхность 2»:

Находим приведенную степень черноты данной системы тел «поверхность 1 – экран»:

Принимаем по приложению 8 для полированного алюминия при t = 575  :
: 

Находим приведенную степень черноты данной системы тел «экран - поверхность 2»:

Определим эффективность действия тепловых экранов, когда 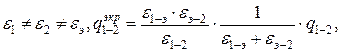 отсюда
отсюда
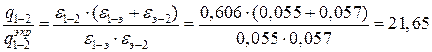 раза.
раза.
Ответ:  = 21,65 раза.
= 21,65 раза.
ВАРИАНТЫ ЗАДАНИЙ
Таблица 1
| Последняя цифра номера зачетки | |||||||||||
| Предпоследняя цифра номера зачетки | |||||||||||
| 51(а) 90(к) 101(б) | 52(а) 89(б) 94(е) | 53(а) 81(б) 95(г) | 54(а) 84(в) 97(д) | 55(а) 86(б) 99(ж) | 56(а) 87(г) 100(б) | 57(а) 69(д) 90(е) 98(б) | 58(а) 71(г) 87(б) 96(и) | 90(а) 97(в) | 51(б) 88(а) 99(б) | ||
| 52(б) 87(а) 102(б) | 53(б) 90(в) 99(а) | 54(б) 81(а) 94(в) | 55(б) 84(а) 102(в) | 56(б) 82(а) 91(д) | 57(б) 65(а) 86(г) 92(е) | 58(б) 89(а) 99(в) | 63(а) 84(г) 100(в) | 51(в) 68(а) 93(б) 96(к) | 52(в) 83(а) 95(д) | ||
| 53(в) 69(а) 88(б) 97(ж) | 54(в) 68(б) 82(д) 96(а) | 55(в) 71(а) 83(б) 92(в) | 56(в) 63(б) 89(д) 101(а) | 57(в) 62(а) 91(б) 99(г) | 58(в) 69(б) 85(а) 101(и) | 60(а) 87(в) 93(ж) | 61(а) 67(д) 85(б) 91(е) | 62(б) 69(г) 82(з) 97(а) | 63(в) 81(ж) 93(а) | ||
| 51(г) 86(а) 100(к) | 52(г) 84(б) 100(а) | 53(г) 67(а) 82(б) 102(б) | 54(г) 68(в) 86(и) 97(б) | 55(г) 71(б) 81(з) 96(д) | 56(г) 62(в) 91(к) 99(з) | 57(г) 64(а) 92(ж) 95(б) | 58(г) 90(и) 98(е) | 51(д) 84(е) 99(к) | 52(д) 67(б) 82(г) 94(а) | ||
| 53(д) 89(в) 98(а) | 54(д) 71(д) 85(в) 97(к) | 55(д) 69(в) 83(ж) 91(а) | 56(д) 65(б) 87(д) 98(и) | 57(д) 61(б) 85(г) 90(ж) | 58(д) 64(б) 89(г) 96(з) | 51(а) 69(г) 88(в) 101(д) | 52(б) 65(д) 89(и) 102(г) | 54(а) 61(в) 86(д) 91(з) | 55(б) 67(в) 93(д) 98(ж) |
Продолжение табл. 1
| Последняя цифра номера зачетки | |||||||||||
| Предпоследняя цифра номера зачетки | |||||||||||
| 52(а) 60(г) 81(в) 99(д) | 51(в) 67(г) 83(и) 96(б) | 54(б) 58(д) 84(д) 93(в) | 55(а) 68(д) 88(г) 95(и) | 62(г) 71(а) 89(ж) 100(з) | 63(д) 82(к) 98(в) | 54(в) 60(д) 85(д) 92(а) | 55(в) 86(е) 94(б) | 56(а) 63(д) 90(б) 100(г) | 57(а) 65(в) 91(г) 97(з) | ||
| 58(б) 67(а) 91(и) 101(в) | 62(б) 65(а) 81(г) 95(ж) | 63(г) 71(б) 89(е) 96(в) | 51(б) 60(б) 82(ж) 99(и) | 52(в) 69(а) 92(б) 97(г) | 53(а) 88(д) 93(е) | 60(в) 69(б) 91(ж) 94(и) | 61(г) 64(в) 81(к) 101(е) | 62(д) 68(а) 83(в) 102(д) | 64(г) 71(в) 86(ж) 90(д) | ||
| 65(г) 71(д) 82(в) 93(г) | 61(д) 69(в) 86(к) 92(д) | 64(д) 90(г) 97(е) | 63(б) 81(д) 100(ж) | 53(б) 61(а) 83(г) 94(ж) | 60(а) 95(з) 101(ж) | 56(б) 68(г) 89(з) 96(ж) | 57(в) 67(г) 91(а) 99(е) | 60(б) 64(а) 92(к) 98(з) | 61(б) 65(г) 83(з) 101(к) | ||
| 55(г) 67(б) 83(д) 96(г) | 54(д) 93(и) 100(д) | 56(в) 64(б) 92(з) 98(г) | 57(б) 68(д) 85(а) 94(г) | 58(а) 65(б) 87(г) 93(з) | 51(г) 61(в) 82(и) 101(з) | 52(г) 68(б) 81(е) 100(и) | 53(в) 71(г) 88(а) 97(и) | 62(а) 89(к) 95(е) | 60(в) 86(з) 92(и) | ||
| 63(а) 69(г) 90(з) 100(е) | 55(д) 64(в) 82(е) 98(д) | 54(г) 67(в) 86(в) 95(к) | 53(г) 65(в) 83(к) 96(е) | 51(д) 57(г) 95(в) 102(а) | 58(г) 68(в) 81(и) 94(з) | 56(д) 64(г) 92(в) 101(к) | 57(д) 71(в) 83(е) 98(к) | 60(г) 63(в) 93(к) 94(д) | 56(г) 69(д) 89(а) 101(в) |
Задачи
Задача 1-10. Определить величину вакуума и абсолютное давление во всасывающей линии ацетиленового компрессора А по показаниям ртутного вакуумметра (рис. 7), если атмосферное давление p атм = 105 Па. Ртуть в левом колене поднялась на высоту h рт. Так как соединение паров ртути с ацетиленом опасно в пожарном отношении, над ртутью налито масло, высота столба которого h м. Плотность ртути ρ = 13,6 · 103 кг/м3; плотность масла ρ = 800 кг/м3.
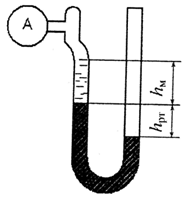
Рисунок 7 - Ртутный вакуумметр.
| Номер задачи | ||||||||||
| Высота столба ртути hрт, м | 0,55 | 0,50 | 0,58 | 0,53 | 0,45 | 0,64 | 0,57 | 0,59 | 0,60 | 0,62 |
| Высота столба масла hм, м | 0,30 | 0,35 | 0,28 | 0,32 | 0,40 | 0,29 | 0,30 | 0,34 | 0,40 | 0,23 |
Задача 11-20. Определить величину силы гидростатического давления Р воды на затвор АВ высотой l шириной в и точку приложения ее результирующей у цд (h цд), если угол наклона стенки равен α, а глубина погружения затвора Н (рис. 8). Построить эпюру давления на затвор и решить задачу аналитическим и графоаналитическим способами.

Рис 8 – Затвор, расположенный на глубине
| Наименование величин и единицы измерений | Номер задачи | |||||||||
| l, м | 2,5 | 1,2 | 1,5 | 2,2 | 2,8 | 1,7 | 2,6 | 2,5 | ||
| в, м | 1,5 | 2,2 | 1,7 | 2,1 | 1,3 | 2,5 | 2,3 | 1,8 | ||
| H, м | ||||||||||
| a, град |
Задача 21-30. По трубопроводу, включающему прямолинейный горизонтальный участок длиной L и диаметром 33·10-3 м, внезапное расширение трубопровода с диаметра 33·10-3 м до 64·10-3 м и внезапное сужение трубопровода с диаметра 64·10-3 м до диаметра 25·10-3 м, протекает вода с расходом Q = 0,6·10-3 м3/c и температурой t. Прямолинейный участок трубопровода и местные сопротивления ограничены соответствующими пьезометрами (рисунок 9), показания которых h 1, h 2, h 3, h 4, h 5, h 6. Определить значения коэффициента трения λ на прямолинейном участке трубопровода и коэффициентов местных сопротивлений для внезапного расширения ζ расш и внезапного сужения ζ суж. Построить пьезометрическую и напорную линии. Определить режимы движения воды на каждом участке трубопровода.
| Номер задачи | ||||||||||
| L, м | 3,6 | 3,7 | 3,8 | 3,9 | 4,0 | 4,1 | 4,2 | 4,3 | 4,4 | 4,5 |
| t, 0C | ||||||||||
| h1, м | 1,56 | 1,57 | 1,58 | 1,78 | 1,79 | 1,80 | 1,33 | 1,34 | 1,35 | 1,32 |
| h2, м | 1,49 | 1,50 | 1,51 | 1,74 | 1,75 | 1,76 | 1,26 | 1,27 | 1,28 | 1,25 |
| h3, м | 1,47 | 1,48 | 1,49 | 1,71 | 1,72 | 1,73 | 1,24 | 1,25 | 1,26 | 1,23 |
| h4, м | 1,48 | 1,49 | 1,50 | 1,72 | 1,73 | 1,74 | 1,25 | 1,26 | 1,27 | 1,24 |
| h5, м | 1,48 | 1,49 | 1,50 | 1,72 | 1,73 | 1,74 | 1,25 | 1,26 | 1,27 | 1,24 |
| h6, м | 1,33 | 1,34 | 1,35 | 1,58 | 1,59 | 1,60 | 1,11 | 1,12 | 1,13 | 1,10 |

Рисунок 9 – Участок трубопровода
Задача 31-40. Определить расход, максимальную и среднюю скорость воздушной струи, выходящей из круглоцилиндрической трубы диаметром d 0 в воздух с начальной скоростью u 0 на расстоянии х 1 от выходного сечения.
| Номер задачи | Диаметр трубы d 0, м. | Начальная скорость воздуха u 0, м/с | Расстояние х 1 от выходного сечения, м. |
| 0,25 | |||
| 0,20 | |||
| 0,21 | |||
| 0,22 | |||
| 0,23 | |||
| 0,24 | |||
| 0,30 | |||
| 0,32 | |||
| 0,34 | |||
| 0,28 |
Задача 41-50. Определить величину избыточного давления в начале магистральной линии длиной L, м, состоящей из пожарных рукавов, диаметром D, мм при расходе воды Q, л/с. Время перекрывания воды составляет τ секунд. Напор в начале рукавной линии составляет H, м.
| Номер задачи | Длина магистральной линии, L, м. | Тип рукавов магистральной линии | Диаметр рукавов, D, мм | Расход воды, Q, л/с | Время перекрытия воды, τ, сек. | Напор, H, м. |
| прорезиненный | ||||||
| латексированный | ||||||
| непрорезиненный | ||||||
| прорезиненный | ||||||
| латексированный | ||||||
| непрорезиненный | ||||||
| прорезиненный | ||||||
| непрорезиненный | ||||||
| латексированный | ||||||
| прорезиненный |
Задачи 51 (а, б, в, г, д). Определить массу метана (CH4), находящегося в аппарате емкостью 500 л, если давление газа по манометру равно: а) 291 кПа; б) 196 кПа; в) 392 кПа; г) 0,6 МПа; д) 0,78 МПа. Температура газа 17 °С. Барометрическое давление при данной температуре равно 99975 Па.
Задача 52 (а, б, в, г, д) Определить удельный объем и плотность метана (CH4), находящегося под давлением 98642 Па, если его температура равна: а) 14 °С, б) 17 0 С, в) 19оС, г) 20°С, д) 24°С.
Задача 53 (а, б, в, г, д). Плотность этилена (C2H4) при нормальных условиях 1,25 кг/м3. Определить плотность этилена, если его давление 0,1 МПа, а температура соответственно равна: а) 10 °С, б) 16 °С, в) 18 °С, г) 22 °С, д) 27 °С.
Задача 54 (а, б, в, г, д). Баллон с кислородом емкостью 60 л при давлении 8 МПа оказался в зоне очага пожара. Масса кислорода 7 кг. Определить, каково будет давление кислорода, если его температура через некоторое время повысилась до: а) 230 °С; б) 277 °С; в) 380 °С ; г) 450 °С; д) 560 °С. Сделать вывод, возможен ли взрыв баллона, если допустимое давление для него 15 МПа.
Задача 55 (а, б, в, г, д). В аппарате емкостью 0,8 мэ находился аммиак (NH3) при давлении 800 кПа и температуре 18 °С. В результате аварии газ вышел наружу. Определить массу вышедшего газа, и какой объем займет аммиак, если его температура осталась неизменной, а давление снизилось до: а) 0,1 МПа; б) 99 кПа; в) 98000 Па, г) 0,097 МПа; д) 96 кПа.
Задача 56 (а, б, в, г, д). Массовый состав смеси следующий: двуокись углерода – 18 %, кислород – 12 %, азот – 70 %, Определить, до какого давления нужно сжать эту смесь, чтобы при температуре 80 °С 8 кг ее занимали объем равный: а) 0,6 м3; б) 0,8 м3; в) 1,2 м3; г) 2 м3; д) 2,5 м3.
Задача 57 (а, б, в, г, д). Определить объемный состав, газовую постоянную и объем смеси, если ее массовый состав следующий: метан – 48,7 %, этилен – 16,8 %, окись углерода – 14,6 %, кислород – 4,7 %, азот – 15,2 %. Давление смеси 0,1 МПа, масса смеси 6 кг, температура смеси соответственно равна: а) 14 °С; б) 17 °С, в) 22 °С; г) 25°С;.д) 27 °С.
Задача 58 (а, б, в, г, д). В помещении объемом 150 м3 при давлении воздуха 0,1 МПа и температуре 17 °С произошло истечение ацетилена (С2Н2). Определить массовые и объемные доли смеси ацетилена с воздухом, а также сделать вывод о возможности образования взрывоопасной концентрации, если пределы воспламенения ацетилена 2,5 и 81 % по объему. Масса ацетилена равна: а) 7 кг; б) 4 кг; в) 3 кг; г) 1,5 кг; д) 1 кг.
Задача 59. Газовая смесь имеет следующий объемный состав: двуокись углерода – 12 %, кислород – 7 %, азот – 75 %, пары воды – 6 %. Определить удельную теплоемкость смеси при постоянном давлении, считая теплоемкость газов, входящих в смесь, постоянной.
Задача 60 (а, б, в, г, д). Азот, находящийся при постоянном давлении 0,2 МПа и температуре 22°С, занимал объем равный: а) 0,5 м3: б) 2 м3; в) 3 м3; г) 4,5 м3; д) 6 м3. В результате пожара температура газа увеличилась до 317 °С. Определить, какой объем займет при этом газ и полученное количество тепла, принимая зависимость теплоемкости от температуры прямолинейной. Вычертить график процесса.
Задача 61 (а, б, в, г, д). 2 м3 ацетилена с начальной температурой 15 °С расширяются при постоянном давлении в результате получения газом 900 кДж теплоты. Определить конечную температуру и объем газа в конце расширения. Теплоемкость ацетилена принять постоянной. Давление газа в процессе соответственно равно: а) 0,15 МПа, 6) 0,2 МПа; в) 0,24 МПа; г) 0,3 МПа; д) 0,4 МПа. Вычертить график процесса.
Задача 62 (а. б, в, г, д). 0,25 кг кислорода при начальном давлении 0,1 МПа сжимается в компрессоре изотермически до давления 20 МПа. Определить конечный объем, затрачиваемую работу и количество отводимого тепла, если температура газа равна: а) 27 °С; б) 32 °С; в) 44 °С; г) 50 °С; д) 62 °С. Вычертить график процесса.
Задача 63 (а. 6, в, г, д). 0,5 м3 воздуха при температуре 27 °С и начальном давлении 500 кПа расширяется изотермически. Определить конечное давление, совершаемую газом работу и количество сообщенной теплоты, если объем газа увеличился в: а) 3 раза: б) 3,5 раза; в) 5 раз; г) 2,8 раза; д) 4 раза. Вычертить график процесса.
Задача 64 (а, б. в, г, д). Установлено, что в результате пожара баллон с кислородом емкостью 60 л может получить количество тепла равное: а) 200 кДж; б) 350 кДж; в) 400 кДж; г) 500 кДж; д) 650 кДж. Определить, до какой температуры нагреется газ и каково при этом будет его давление, если известно, что начальная температура кислорода 17 °С, начальное давление. 15 МПа, а удельную теплоемкость при постоянном объёме, равную 0,654 кДж/(кг К), можно принять постоянной. Вычертить график процесса.
Задача 65 (а. 6. в, г, д). Баллон с этиленом емкость 40 л при давлении 6 МПа и начальной температуре 20 СС оставлен у системы парового отопления. Через некоторое время температура газа поднялась до: а) 32 °С; б) 40 °С; в) 45 °С; г) 27 °С, д) 57 °С. Определить, каково будет давление газа при этом и количество полученной теплоты, принимая удельную теплоемкость этилена постоянной. Вычертить график процесса.
Задача 66. Какое количество тепла надо сообщить 1,2 кг двуокиси углерода (СО2) при постоянном объеме для повышения давления от 0,1 до 0,3 МПа, если объем сосуда 0.65 м3. Зависимость теплоемкости от температуры – прямолинейная. Вычертить график процесса.
Задача 67 (а, б, в, г, д) Какое количество тепла необходимо отвести от баллона с водородом емкостью 80 л, чтобы температура газа понизилась от 600 °С до: а)27°С; б) 38 °С; в) 46 °С; г) 52 °С, д) 60 °С. Каково при этом установится давление в баллоне? Масса газа 0,5 кг. Теплоемкость водорода принять постоянной.
Задача 68 (а б, в, г, д). 1 м3 воздуха при постоянном давлений 0,16 МПа подогревается от 100 °С до: а) 200 °С; б) 300 °С; в) 400 °С; г) 500 °С; д) 600 °С. Определить конечный объем воздуха и количество затраченного тепла, принимая зависимость теплоемкости от температуры нелинейной. Вычертить график процесса.
Задача 69 (а, б, в, г,д). Азот при давлении 0,9 МПа и температуре 100 °С нагревается в аппарате при постоянном объеме 6 м3 до. а) 200°С, б) 250 °С; в) 300 °С; г; 350 °С, д) 400 °С. Определить конечное давление газа и количество подведенной теплоты, принимая зависимость теплоемкости от температуры нелинейной. Вычертить график процесса.
Задача 70. 5 м3 кислорода при давлении 98,6 кПа и температуре 20 °С изотермически сжимается до давления 0,8 МПа Определить конечный объем, затраченную работу и количество отведенного тепла. Вычертить график процесса.
Задача 71. (а, б, в, г, д). 100 м3 окиси углерода (СО) при температуре 327 °С и постоянном давлении 0;7 МПа охлаждаются до: а) 17 °С; б) 23 °С, в) 27 °С; г) 35 °С; д) 45° С. Определить количество отведенной теплоты, принимая зависимость теплоемкости от температуры прямолинейной. Вычертить график процесса.
Задача 72. В воздухоподогревателе котельной установки воздух нагревается от 50 до 200 °С при постоянном давлении. Определить количество теплоты, необходимое для нагревания 1 кг воздуха и удельную работу расширения, принимая теплоемкость постоянной, зависящей от температуры прямолинейно и зависящей от температуры нелинейно. Сделать вывод, какой зависимостью теплоемкости от температуры необходимо пользоваться для получения более точных расчетов? Вычертить график процесса.
Задача 73. 1 кг воздуха сжимается в цилиндре адиабатно, объём воздуха при этом уменьшается в 14 раз. Определить конечную температуру и конечное давление воздуха, если начальная температура его 100 °С, а начальное давление 0,1 МПа. Показатель адиабаты принять равным 1,4. Вычертить график процесса.
Задача 74. 2 кг азота при давлении 0,1 МПа и температуре 15 °С адиабатно сжимаются в цилиндре до давления 0,7 МПа. Определить конечную температуру и работу, затраченную на сжатие, принимая показатель адиабаты равным 1,4. Вычертить график процесса.
Задача 75. 3 м3 метана (СH4) при температуре 150 °С расширяются политропно. При этом давление газа изменяется от 0,54 до 0,12 МПа, а объем увеличивается до 10 м3. Определить показатель политропы, конечную температуру и совершенную газом работу. Вычертить график процесса,
Задача 76. 1кг воздуха совершает прямой цикл Карно в пределах температур 627 °С и 27 °С При этом наибольшее давление равно 5 МПа, а наименьшее – 0,1 МПа. Определить параметры состояния воздуха в характерных точках цикла и количество отведенной теплоты, принимая показатель адиабаты 1,4. Построить данный цикл графически.
Задача 77. Определить параметры характерных точек для цикла двигателя внутреннего сгорания с подводом тепла при постоянной объеме и термический к. п. д. цикла, если известно: рабочее тело – воздух массой 1 кг, в точке 1 давление равно 0,1 МПа, а температура 80 °С; степень сжатия равна 6, степень повышения давления 1,8; показатель адиабаты принять равным 1,4. Построить диаграмму цикла. Сравнивая температуру в момент выхлопа с температурой воспламенения некоторых распространенных горючих материалов, сделать вывод о степени пожарной опасности данного двигателя.
Задача 78. В результате аварий из аппарата наполненного кислородом при давлении 0,12 МПа и температуре 50 °С, происходит истечение газа наружу. Площадь отверстия 10 мм2. Давление среды, в которую происходит истечение, равно 96000 Па. Определить теоретическую скорость истечения кислорода и секундный массовый расход газа. Показатель адиабаты принять 1,4. Начальную скорость истечения принять равной нулю.
Задача 79. Для ликвидации горения продукта в реакторе предусмотрена подача азота. Определить требуемую площадь выходного сечения сопла, через которое будет происходить истечение газа в реактор, если известно: давление азота 0,5 МПа, давление среды в реакторе 0,3 МПа, температура азота 27 °С, требуемый секундный расход газа 0,2 кг/с. Показатель адиабаты принять 1,4.
Задача 80. Через образовавшееся в результате аварии в корпусе аппарата отверстие площадью 20 мм2 происходит истечении этилена в объем помещения. Давление газа 5 МПа, температура газа в аппарате 20 °С, давление среды, в которую происходит истечение, 0,1 МПа. Определить критическую скорость истечения и максимальный массовый расход этилена, принимая показатель адиабаты 1,29.
Задача 81(а, б, в, г, д, е, ж, з, и, к). Определить требуемую толщину теплоизоляции стального трубопровода, чтобы температура на наружной поверхности теплоизоляции не превышала 80 °С. Материал – асбоцементные скорлупы (полуцилиндры). Диаметр трубопровода 0,15 м. Плотность теплового потока и температура на внутренней поверхности теплоизоляции соответственно равны:
| Задача | а | б | в | г | д | е | ж | з | и | к |
| Плотность теплового потока, Вт/м | ||||||||||
| Температура внутренней поверхности,°С |
Задача 82 (а, б, в, г: д, е, ж, з, и, к). Определить коэффициент теплообмена при естественной конвекции между дымовыми газами и вертикальной стенкой помещения высотой 3 м, если температура дымовых газов и поверхности стенки соответственно равны:
| Задача | а | б | в | г | д | е | ж | з | и | к |
| Температура дымовых газов, °С | ||||||||||
| Температура стенки, °С |
Задача 83 (а, б, в, г; д, е, ж, з, и, к). Противопожарная закрытая отступка печи имеет размер 0,13 м. Определить плотность теплового потока от поверхности печи к поверхности деревянной перегородки в конвективном теплообмене, если температура поверхности печи и поверхности перегородки соответственно равны:
| Задача | а | б | в | г | д | е | ж | з | и | к |
| Температура поверхности печи, °С | ||||||||||
| Температура поверхности перегородки,°С |
Задача 84 (а, б, в, г; д, е). В цистерне пожарного автомобиля для подогрева воды выхлопными газами смонтирован трубопровод. Дымовые газы при средней температуре 300°С движутся со скоростью 10 м/с. Отношение l / d нар > 50. Определить коэффициент теплообмена конвекцией между дымовыми газами и внутренней поверхностью трубопровода, если его внутренний диаметр равен: а) 25 мм, б) 38 мм: в) 45 мм; г) 60 мм, д) 80 мм, е) 90 мм.
Задача 85 (а, б, а, г, д). Расположение теплоотдающей поверхности нетеплоемкой печи и поверхности деревянной перегородки представляет собой случай плоскопараллельных поверхностей. Степень черноты поверхности печи 0,8; степень черноты поверхности древесины 0,9. Определить плотность теплового потока и сделать вывод о возможности воспламенения древесины, если критическая плотность облучения древесины 12800 Вт/м2, температура самовоспламенения 530 К, а температура излучающей поверхности печи равна: а) 620 К; б) 700 К; в) 780 К; г) 830 К, д) 870 К.
Задача 86. (а, б, а, г, д, е, ж, з, и, к). Определить эффективность применения теплового экрана из полированного алюминия, установленного между стенкой печи из шамотного кирпича и деревянной конструкцией, если температура поверхности кирпичной кладки и поверхности деревянной конструкции соответственно равна:
| Задача | а | б | в | г | д | е | ж | з | и | к |
| Температура кирпичной кладки, °С | ||||||||||
| Температура деревянной конструкции,°С |
Предельно допустимая температура для материала экрана 873 К. Значения степени черноты указанных материалов принять по приложению 8.
Задача 87 (а, б, а, г, д). Определить требуемое количество экранирующих слоев из шлифованной листовой стали для защиты деревянной конструкции от лучистой тепловой энергии, если степень черноты излучающей поверхности 0,8, плотность теплового потока от излучающей поверхности равна а) 32000 Bт/м2; б) 45000 Вт/м2, в) 52000 Вт/м2; г) 56000 Вт/м2, д) 60000 Вт/м2. Степень черноты материала экрана, сосновой шероховатой древесины и критическую плотность теплового потока для древесины выбрать по приложениям 8, 9.
Задача 88 (а, б, в, г, д). Дать заключение о достаточности противопожарного разрыва между двумя штабелями сосновой шероховатой древесины, если возможные размеры факела при пожаре 6×12 м, температура факела 1300 К, предельно допускаемая температура древесины 530 К, величина противопожарного разрыва в м соответственно равна: а) 4: б) 6, в) 8; г) 10; д) 12. Коэффициент безопасности 1,2; степень черноты древесины и критическую плотность облучения выбрать по соответствующим приложениям.
Задача 89 (а, б, в, г, д, е, ж, з, и, к) Определить требуемую величину противопожарной разделки дымохода из красного кирпича (рис. 10). исходя из условия, что температура в месте соприкосновения разделки с горючим материалом перекрытия не должна превышать 80 °С; температура нагреваемой среды (окружающего воздуха) равна 10 °С; температура нагретой среды (отходящих газов) соответственно равна:
| Задача | а | б | в | г | д | е | ж | з | и | к |
| Температура нагретой среды, °С |

Рисунок 10 – Схема к задаче 89
Задача 90 (а, б, в, г, д, е, ж, з, и, к) Определить температуру на наружной поверхности дымохода из красного кирпича и сделать вывод с точки зрения пожарной безопасности, если толщина стенки дымохода равна 0,25 м; температура окружающего воздуха 15 °С, температура отходящих газов соответственно равна:
| Задача | а | б | в | г | д | е | ж | з | и | к |
| Температура отходящих газов, °С |
Задача 91 (а, б, в, г, д, е. ж, з, и, к). Определить требуемую толщину бетонной стены, если коэффициент теплопроводности бетона равен 0,84 Вт/(м·К); температура нагреваемой среды 20 °С, температура на необогреваемой поверхности стены не должна превышать 160 °С, температура нагретой среды при возможном пожаре соответственно равна:
Не нашли, что искали? Воспользуйтесь поиском: