Основные математические обозначения

Основы системного анализа и управления в таможенном деле».

Таблицы и схемы.

Основные математические обозначения

Формульные обозначения и их трактовка

Обозначение	Трактовка
a Î A, A ' a	элемент а принадлежит множеству А (множество А содержит элемент a)
a Ï A	элемент а не принадлежит множеству А (множество А не содержит элемент а)
A = { a, b, c }	множество А состоит из элементов a, b, c
A º { a }	множество А состоит из элементов ai, i = 1, 2, …, n
A = { x: … } A = { x ç … }	множество А состоит из элементов x, обладающих свойством, указанным после двоеточия (вертикальной черты)
A = Æ	множество А пусто
A Ì B, B É A	подмножество А включено в множество В (В включает А)
A Í B, B Ê A	подмножество А включено в множество В (совпадает с ним)
N	множество натуральных чисел
Z	множество целых чисел
Q	множество рациональных чисел
R	множество действительных чисел
[ a, b ]	отрезок с концами в точках a и b
(a, b)	интервал с концами в точках a и b
[ a, b), (a, b ]	полуинтервалы с концами в точках a и b
çxç	абсолютное значение числа x
+¥, -¥	бесконечные точки расширенной числовой прямой
(- ¥, + ¥), (- ¥, a), (b, +¥)	бесконечные интервалы
(- ¥, a], [b, +¥)	бесконечные полуинтервалы
	объединение множеств А и В
	пересечение множеств А и В
A \ B	разность множеств А и В
	объединение N множеств А 1, …, Аn,… AN
	пересечение N множеств А 1, …, Аn,… A N
A Þ B	из А следует В (А – необходимое условие В; В – достаточное условие А)
A Û B	высказывания А и В равносильны
: Û	утверждение справедливо по определению
Ú и Ù	символы дизъюнкции (союз «или») и конъюнкции (союз «и»)
$ x: …	существует такое x, что…
" x	для любого x
¦: X ® Y	отображение ¦ множества X на (в) множество Y
¦(a)	значение функции ¦(x) в точке a
D (¦)	область определения (существования) функции ¦(x)
R (¦)	область значений функции ¦(x)
x = ¦-1(y)	функция, обратная функции y = ¦(x)
M (x, y)	точка М плоскости с координатами x (абсцисса) и y (ордината)
	сумма n слагаемых a 1, …, ak, …, an
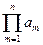
	произведение n сомножителей a 1, …, am, …, an
Pn	количество перестановок из n элементов
	количество сочетаний из n элементов по k
k =	k = 1, 2, …, n – число k принимает последовательно все значения из множества натуральных чисел от 1 до n включительно
sup Х, sup x x Î X	точная верхняя грань множества Х
inf Х, inf x x Î X	точная нижняя грань множества Х
sup ¦ (x) x Î X	наибольшее значение функции ¦ (x) на множестве Х
inf ¦ (x) x Î X	наименьшее значение функции ¦ (x) на множестве Х
∆ x, ∆ y = ∆ f (x)	приращение аргумента х и функции f (x)
¦ (x) ≈ g (x) x → a	функции ¦ (x) и g (x) эквивалентны при x → a

Буквы греческого алфавита

Тема «Введение в курс»

Не нашли, что искали? Воспользуйтесь поиском: