Кездейсоқ сандар

Монте-Карло әдісімен заттағы бөлшекетрдің траекторияларын модельдеу үшін нақты физикалық заңдарға сәйкес таралумен кездейсоқ сандар қажет. Модельдеу үшін қажетті кездейсоқ сандардың барлық түрлерінің жиынтықтарын (0,1) интервалда бірқалыпты таралған кездейсоқ сандарды γ түрлендіру арқылы алуға болады. Таралу тығыздығы осы интервалда тұрақты болатын мұндай сандар стандартты кездейсоқ сандар деп аталады.

Қолданылатын кездейсоқ сандардың «сапасына» қойылатын талаптар өте қатал. Олардың қайталану периоды кем дегенде 10⁶–10⁷ сан болуы керек. Осы талап бұзылған кезде модельдеу нәтижелері бұзылады. Сондықтан кездейсоқ сандарды алу үшін тек қана жан-жақты зерттеулерді және апробацияланған (қабылданған, мақұлданған) алгоритмдерді қолдануға болады.

Стандартты кездейсоқ сандарды алудың бірнеше алгоритмдері бар. Осы мақсат үшін көбінесе nR түрдегі бөлшек сандар (0,1) интервалда біркелкі таралған сандар тізбегі болып табылады дегене тұжырымды растайтын теорема қолданылады, бұл жерде R – кез келген иррационал сан. Әдетте кездейсоқ сандардың бағдарламалық датчиктерінде рекурентты формула қолданылады:

Осы формулаға сәйкес шамасы -ді -ге бөлгендегі қалдыққа тең. Бұл кезде . , а және сандары арнайы таңдалынып алынады. Әдетте , р – тұтас. Кездейсоқ сандар -ді -ге бөліп алынады.

Бағдарламалық жолмен рекурентті қатынастардың көмегімен алынатын кездейсоқ сандарды жалған кездейсоқ деп атайды, себебі қатаң түрде олар кездейсоқ болып табылмайды.

Стандартты кездейсоқ сандарды алу үшін бағдарламалар кез келген заманауи ЭЕМ математикалық қамтамасыз ету жүйесінде бар болады.

Стандартты кездейсоқ шамалар бойынша берілген таралуымен кездейсоқ сандарды алудың ең көп таралған әдісі – кері функциялар әдісі. Бұл әдістің мағынасы 1 суретте түсінідіріледі.

Бірқалыпты артатын f(x)функциясы f(a)=0, f(b)=1 мәндерін қабылдасын. Стандартты кездейсоқ санның γ әрбір мәніне мәнін табуға болады. Алынған сандар тығыздығы таралу функциясынан есептеуге болатын кездейсоқ сандар болады

(1.1)

себебі .

Кері функциялар әдісі (1.1) интегралын элементар функцияларда алуға болатын кезде ыңғайлы болып табылады. Мысалы, егер

(1.2)

онда , бұл жерден . Олай болса,

(1.3)

(a, b) интервалында біркелкі таралатын ξ кездейсоқ сандар үшін осфлай сияқты келесі өрнекті алуға болады

(1.4)

Кері функциялар әдісін егер f(x)функциясы тек сандық берілген жағдайда да қолдануға болады. Онда тепе-тең тұратын мәндерін интерполяциялап 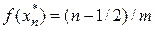біркелкі таралған функциясының реттілігіне сәйкес келетін жиынтығын алады, бұл жерде n=1m 2, 3, …, m. мәні жадқа енгізіледі, және ұяшығының нөмірі табылады.

Кейбір алгоритмдерде 1/f(x)элементар ұяшықтарда берілмеген кезде Нейман әдісі қолданылады. Оның мағынасы келесідей болады. Ықтималдық тығыздығы болатын ξ кездейсоқ сан [a, b] аралығында таралсын. [a, b] және [0, m] кесінділерде γ₁ және γ₂ кездейсоқ сандары таңдалынсын, бұл жерде 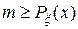. Олай болса, егер болса, онда . Олай болмаса γ₁ және γ₂ таңдау процесі қайталанады.

Кері функциялар әдісі және Нейман әдісімен қатар кездейсоқ шамаларды түрлендіретін бірқатар арнайы әдістер бар.

Қорытынды:

Ғылыми әдебиеттермен танысып және диссертация тақырыбы бойынша ғылыми зерттеу жұмысына пайдаланатын бағдарламаны игердім. Тұрақты ядролық реакторға белсенді аймақта жылулық нейтрондардың ағынмен белсенді ядролық реакциялардың өнімдермен құрастырылған электр теріс плазманы эксперименталді және теориялық зерттеудің маңыздылығын түсіндім. Монте-Карло әдісі бойынша электрондардың энергетикалық таралуының бағдарламалық кодын жасақтауға жұмыстар жүргіздім.

Қолданылған әдебиеттер тізімі

1. Биндер К., Хеерман Д.В. Моделирование методом Монте-Карло в статистической физике.1995,144с.

2. Чен Ф. Электрические зонды //Диагностика плазмы // Под редакцией Р. Хаддлстоуна и С.Леонарда, Диагностика плазмы.М:Мир,1967, Langmuir I.,Phys.Rev.,28,727(1926)

3. Чен П., Телбот Л., Турян К. Электрические зонды в неподвижной и движущейся плазме.Изд.Мир,1978

4. Bohm D. The Characteristics of Electrical Discharges in Magnetic Fields, ed. A.Gurthrie, R.K. Wakerling, New York.1940

5. Ульянов К.Н. Теория электрических зондов в плотной азме.ЖТФ,1970,№40,вып.4,стр.790

Не нашли, что искали? Воспользуйтесь поиском: