Тақырып: Екі өлшемді массивтерді қолдану арқылы программа құру.

Зертханалық сабақ тапсырмасы:

1. n натурал саны, n реттік өлшемдегі нақты шаршы матрица нақты сандары берілген. Егер матрицаның ең үлкен мәнді элементі басты диагональда орналасқан болса, онда тізбегінің элементтерін 10-ға көбейту керек, кері жағдайда 0,5-ке.

2. нақты сандары мен n өлшемдегі нақты шаршы матрицасы берілген. 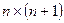өлшемдегі нақты шаршы матрицасын бастапқы матрицаға бесінші мен алтыншы бағаналар арасына элементті жаңа бағанды қосу арқылы құру.

3.. өлшемдегі бүтінсандық шаршы матрицасы берілген. Жаңа матрицаны келесі ереже бойынша құру:

а) бағаналарын орындарымен ауыстыру арқылы біріншіні соңғысымен, екіншіні соңғысының алдындағысымен және т.с.с;

ә) қатарларын орындарымен ауыстыру арқылы біріншіні соңғысымен, екіншіні соңғысының алдындағысымен және т.с.с;

4. n өлшемдегі нақты шаршы матрицасы берілген. Матрицаны келесі ереже бойынша түрлендіру: n нөмірлі қатарды n нөмірлі баған етіп, ал n нөмірлі бағанды керісінше n нөмірлі қатар етіп.

5 n өлшемдегі екі нақты шаршы матрицалары берілген. Жаңа матрицаны келесі ереже бойынша алу:

а) бірінші матрицаның әр қатарының элементтерін екінші матрицаның әр қатарының ең үлкен мәнді элементіне көбейту арқылы;

ә) бірінші матрицаның әр бағанының элементтеріне екінші матрицаның тиісінше әр бағанының элементтерінің көбейтіндісін қосу арқылы.

6. Берілген n өлшемді нақты шаршы матрицадан модулі бойынша ең үлкен элементті табу керек. Бастапқы матрицадан табылған элемент орналасқан қатар мен бағананы жою арқылы N-1 өлшемдегі нақты шаршы матрицасын алу.

7. Элементтерінің мәні әр түрлі болып келетін n өлшемдегі нақты шаршы матрицасы берілген. Оның басты және кері диагональ элементтерінің арасынан ең үлкен мәндісін анықтау және оны диагональдар қиылысқан жердегі элементпен ауыстыру.

8. n реттік нақты шаршы матрица берілген. Суретте көрсетілгендей боялған аумақтың элементтерінің арасынан ең үлкенін табу керек (1-сурет):

1-сурет.

9 2n өлшемдегі нақты шаршы матрицасы берілген. өлшемдегі жаңа матрицаны оның блоктарын ауыстыру арқылы алу (2-сурет)

2-сурет.

10. және өлшемдегі А және В матрицалары берілген. АВ матрицасын ал.

11. n реттік шаршы матрица берілген. матрицасын ал.

12. n реттік шаршы А және В матрицалары берілген. АВ-ВА матрицасын ал.

13. n реттік шаршы А матрицасы мен n элементті вектор берілген. Келесі векторларды алу керек: а) ; б) в) , мұндағы Е – n -ші ретті бірлік матрица.

14. n реттік шаршы А,В және С матрицалары берілген. (А+В)С матрицасын алу.

15. n реттік шаршы А,В матрицалары берілген. А(В-Е)+С матрицасын алу, мұндағы Е - n- реттік бірлік матрица, ал С матрицаның элементтері: формуласымен анықталады.

16. өлшемдегі нақты А матрицасы берілген. одан (оның өлшемі - ) транспонирленген матрицасын алу.

17. n реттік шаршы матрица берілген. Ab векторын алу керек, мұндағы b - вектор, оның элементтері формула бойынша есептелінеді:

а) б) ;

18. n реттік А шаршы матрицасы берілген. АВ матрицасын алу ; В матрицасының элементтері келесі формула бойынша есептеледі:

а) б) ; в)

19. А матрицасы берілген:

а) өлшемді ә) өлшемді

өлшемді матрицаны есептеу керек.

20. m реттік квадраттық А матрицасы берілген. Келесі матрицаларды алу керек: және

21. Шаршы матрицаның ізі болып басты диагональда орналасқан элементтердің қосындысы табылады. n натурал саны мен m өлшемді шаршы матрицалар берілген. матрицаларының ізін анықтаңыздар.

22. n өлшемді А оң үшбұрышты матрицасы (n+1)n/2 сандар тізбегі түрінде келесідей берілген: басында бірінші қатардың n элементі, сосын екінші қатардың екінші элементінен бастағандағы n-1 элементі және т.с.с. (соңғы n - қатардан тек n -ші элемент алынады). Бұдан басқа n элементті b векторы беріледі. Ab векторын анықта.

23. Жоғарғы есепте сипатталғандай n реттік А және В екі оң үшбұрышты матрицалары берілген. Келесі матрицаларды алу керек:

а) АВ матрицасын;

б) матрицасын алу, мұндағы Е - n реттік бірлік матрица.

Не нашли, что искали? Воспользуйтесь поиском: