ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Основные свойства средней арифметической величины
1. Произведение средней величины и суммы частот равно сумме произведений значений (вариант) признака на частоты
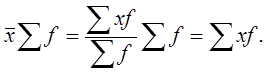
2. Если из каждой варианты вычесть какое-либо произвольное число, то новая средняя уменьшается на то же число
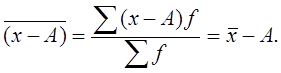
Тогда средняя величина исходных значений
3. Если к каждой варианте прибавить какое-либо произвольное число, то новая средняя увеличится на то же число
Тогда средняя величина исходных значений
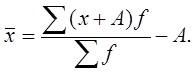
4. Если каждую варианту разделить на какое-либо произвольное число, то средняя арифметическая уменьшится во столько же раз
Тогда средняя величина исходных значений
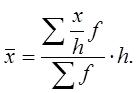
5. Если каждую варианту умножить на какое-либо произвольное число, то средняя арифметическая увеличится во столько же раз
Тогда средняя величина исходных значений
6. Если все частоты умножить (разделить) на какое-либо число, то средняя не изменяется
7. Если все варианты имеют одинаковую частоту (f 1 = f 2 = …= fn = k), то средняя арифметическая взвешенная равна средней арифметической простой
8. Сумма отклонений, как от простой, так и от взвешенной средней арифметической равна нулю
Использование свойств 2 и 4 позволяет значительно упростить расчеты и вычислить арифметическую среднюю в сгруппированном ряду распределения по формуле
где m 1 - момент первого порядка
Метод упрощенного расчета средней величины называется методом отсчета от условного нуля или способом моментов.
Степенные средние используются для расчета хронологических, многомерных и других средних показателей.
Средняя хронологическая является характеристикой ряда динамики и рассчитывается для интервальных и моментных рядов с равноотстоящими и неравноотстоящими уровнями (см. п. 1.4 «Показатели рядов динамики»).
Средняя многомерная величина рассчитывается для каждой i -й единицы статистической совокупности по формуле
где k - количество признаков, характеризующих единицу статистической совокупности; 
- нормированное значение j -го признака i -й единицы совокупности, определяется следующим образом
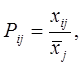
где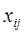 
- значение j -го признака i -й единицы статистической совокупности; 
- среднее значение j -го признака в статистической совокупности.
Не нашли, что искали? Воспользуйтесь поиском: