Методология экспериментальных исследований

Наиболее важной составной частью научных исследований являются эксперименты. Это один из основных способов получить новые научные знания. Более 2/3 всех трудовых ресурсов науки затрачивается на эксперименты. В основе экспериментального исследования лежит эксперимент, представляющий собой научно поставленный опыт или наблюдение явления в точно учитываемых условиях, позволяющих следить за его ходом, управлять им, воссоздавать его каждый раз при повторении этих условий. От обычного, обыденного, пассивного наблюдения эксперимент отличается активным воздействием исследователя на изучаемое явление.

Основной целью эксперимента является проверка теоретических положений (подтверждение рабочей гипотезы), а также более широкое и глубокое изучение темы научного исследования.

Эксперимент должен быть проведен по возможности в кратчайший срок с минимальными затратами при самом высоком качестве полученных результатов.

Различают эксперименты естественные и искусственные.

Естественные эксперименты характерны при изучении социальных явлений (социальный эксперимент) в обстановке, например, производства, быта и т. п.

Искусственные эксперименты широко применяются во многих естественнонаучных исследованиях. В этом случае изучают явления, изолированные до требуемой степени, чтобы оценить их в количественном и качественном отношениях.

Иногда возникает необходимость провести поисковые экспериментальные исследования. Они необходимы в том случае, если затруднительно классифицировать все факторы, влияющие на изучаемое явление вследствие отсутствия достаточных предварительных данных. На основе предварительного эксперимента строится программа исследований в полном объеме.

Экспериментальные исследования бывают лабораторные и производственные.

Лабораторные опыты проводят с применением типовых приборов, специальных моделирующих установок, стендов, оборудования и т. д. Эти исследования позволяют наиболее полно и доброкачественно, с требуемой повторяемостью изучить влияние одних характеристик при варьировании других. Лабораторные опыты в случае достаточно полного научного обоснования эксперимента (математическое планирование) позволяют получить хорошую научную информацию с минимальными затратами. Однако такие эксперименты не всегда полностью моделируют реальный ход изучаемого процесса, поэтому возникает потребность в проведении производственного эксперимента.

Производственные экспериментальные исследования имеют целью изучить процесс в реальных условиях с учетом воздействия различных случайных факторов производственной среды.

Одной из разновидностей производственных экспериментов является собирание материалов в организациях, которые накапливают по стандартным формам те или иные данные. Ценность этих материалов заключается в том, что они систематизированы за многие годы по единой методике. Такие данные хорошо поддаются обработке методами статистики и теории вероятностей.

В ряде случаев производственный эксперимент эффективно проводить методом анкетирования. Для изучаемого процесса составляют тщательно продуманную методику. Основные данные собирают методом опроса производственных организаций по предварительно составленной анкете. Этот метод позволяет собрать очень большое количество данных наблюдений или измерений по изучаемому вопросу. Однако к результатам анкетных данных следует относиться с особой тщательностью, поскольку они не всегда содержат достаточно достоверные сведения.

В зависимости от темы научного исследования объем экспериментов может быть разным. В лучшем случае для подтверждения рабочей гипотезы достаточно лабораторного эксперимента, но иногда приходится проводить серию экспериментальных исследований: предварительных (поисковых), лабораторных, полигонных на эксплуатируемом объекте.

В ряде случаев на эксперимент затрачивается большое количество средств. Научный работник производит огромное количество наблюдений и измерений, получает множество диаграмм, графиков, выполняет неоправданно большое количество испытаний.

На обработку и анализ такого эксперимента затрачивается много времени. Иногда оказывается, что выполнено много лишнего, ненужного. Все это возможно, когда экспериментатор четко не обосновал цель и задачи эксперимента. В других случаях результаты длительного, обширного эксперимента не полностью подтверждают рабочую гипотезу научного исследования. Как правило, это также свойственно для эксперимента, четко не обоснованного целью и задачами. Поэтому прежде чем приступить к экспериментальным исследованиям, необходимо разработать методологию эксперимента.

Методология эксперимента – это общая структура (проект) эксперимента, т. е. постановка и последовательность выполнения экспериментальных исследований. Методология эксперимента включает в себя следующие основные этапы:

1) разработку плана-программы эксперимента;

2) оценку измерений и выбор средств для проведения эксперимента;

3) проведение эксперимента;

4) обработку и анализ экспериментальных данных.

Приведенное количество этапов справедливо для традиционного эксперимента. В последнее время широко применяют математическую теорию эксперимента, позволяющую резко повысить точность и уменьшить объем экспериментальных исследований.

В этом случае методология эксперимента включает такие этапы: разработку плана-программы эксперимента; оценку измерения и выбор средств для проведения эксперимента; математическое планирование эксперимента с одновременным проведением экспериментального исследования, обработкой и анализом полученных данных.

Теперь остановимся несколько поподробней на этапах экспериментального исследования.

План-программа включает наименование темы исследования, рабочую гипотезу, методику эксперимента, перечень необходимых материалов, приборов, установок, список исполнителей эксперимента, календарный план работ и смету на выполнение эксперимента. В ряде случаев включают работы по конструированию и изготовлению приборов, аппаратов, приспособлений, методическое их обследование, а также программы опытных работ на предприятиях.

Основа плана-программы – методика эксперимента. Один из наиболее важных этапов составления плана-программы – определение цели и задач эксперимента. Четко обоснованные задачи – это весомый вклад в их решение. Количество задач должно быть небольшим. Для конкретного (не комплексного) эксперимента оптимальным количеством является 3–4 задачи. В большом, комплексном эксперименте их может быть 8–10.

Необходимо правильно выбрать варьирующие факторы, т. е. установить основные и второстепенные характеристики, влияющие на исследуемый процесс. Вначале анализируют расчетные (теоретические) схемы процесса. На основе этого классифицируют все факторы и составляют из них убывающий по важности для данного эксперимента ряд. Правильный выбор основных и второстепенных факторов играет важную роль в эффективности эксперимента, поскольку эксперимент и сводится к нахождению зависимостей между этими факторами. В тех случаях, когда трудно сразу выявить роль основных и второстепенных факторов, выполняют небольшой по объему поисковый эксперимент.

Основным принципом установления степени важности характеристики является ее роль в исследуемом процессе. Для этого изучают процесс в зависимости от какой-то одной переменной при остальных постоянных. Такой принцип проведения эксперимента оправдывает себя лишь в тех случаях, когда переменных характеристик мало – 1 – 3. Если же переменных величин много, целесообразно применить принцип многофакторного анализа.

Обоснование средств измерений – это выбор необходимых для наблюдений и измерений приборов, оборудования, машин, аппаратов и пр. Средства измерения могут быть выбраны стандартные или в случае отсутствия таковых – изготовлены самостоятельно.

Очень ответственной частью является установление точности измерений и погрешностей. Методы измерений должны базироваться на законах специальной науки – метрологии.

В методике подробно проектируют процесс проведения эксперимента. В начале составляют последовательность (очередность) проведения операций измерений и наблюдений. Затем тщательно описывают каждую операцию в отдельности с учетом выбранных средств для проведения эксперимента. Особое внимание уделяют методам контроля качества операций, обеспечивающих при минимальном (ранее установленном) количестве измерений высокую надежность и заданную точность. Разрабатывают формы журналов для записи результатов наблюдений и измерений.

Важным разделом методики является выбор методов обработки и анализа экспериментальных данных. Обработка данных сводится к систематизации всех цифр, классификации, анализу. Результаты экспериментов должны быть сведены в удобочитаемые формы записи – таблицы, графики, формулы, номограммы, позволяющие быстро и доброкачественно сопоставлять полученные результаты.

Особое внимание в методике должно быть уделено математическим методам обработки и анализу опытных данных – установлению эмпирических зависимостей, аппроксимации связей между варьирующими характеристиками, установлению критериев и доверительных интервалов и др.

После установления методики находят объем и трудоемкость экспериментальных исследований, которые зависят от глубины теоретических разработок, степени точности принятых средств измерений. Чем четче сформулирована теоретическая часть исследования, тем меньше объем эксперимента.

Возможны три случая проведения эксперимента.

Первый – теоретически получена аналитическая зависимость, которая однозначно определяет исследуемый процесс. Например, у = 6е~^5х.

В этом случае объем эксперимента для подтверждения данной зависимости минимален, поскольку функция однозначно определяется экспериментальными данными.

Второй случай – теоретическим путем установлен лишь характер зависимости. Например, у = ае~ ^kх.

В этом случае задано семейство кривых. Экспериментальным путем необходимо определить а и k. При это объем эксперимента возрастает.

Третий случай – теоретически не удалось получить каких-либо зависимостей. Разработаны лишь предположения о качественных закономерностях процесса. Во многих случаях целесообразен поисковый эксперимент. Объем экспериментальных работ резко возрастает. Здесь уместен метод математического планирования эксперимента.

На объем и трудоемкость существенно влияет вид эксперимента. Полевые эксперименты, как правило, имеют большую трудоемкость. После установления объема экспериментальных работ составляют перечень необходимых средств измерений, объем материалов, список исполнителей, календарный план и смету расходов. План-программу рассматривает научный руководитель, обсуждают в научном коллективе и утверждают в установленном порядке.

Проведение эксперимента является важнейшим и наиболее трудоемким этапом. Экспериментальные исследования необходимо проводить в соответствии с утвержденным планом-программой и особенно методикой эксперимента. Приступая к эксперименту, окончательно уточняют методику его проведения, последовательность испытаний.

При сложном эксперименте часто возникают случаи, когда ожидаемый результат получают позже, чем предусматривается планом. Поэтому научный работник должен проявить терпение, выдержку, настойчивость и довести эксперимент до получения результатов.

Особое значение имеет добросовестность при проведении экспериментальных работ; недопустима небрежность, что приводит к большим искажениям, ошибкам. Нарушения этих требований – к повторным экспериментам, что продлевает исследования.

Обязательным требованием проведения эксперимента является ведение журнала. Форма журнала может быть произвольной, но должна наилучшим образом соответствовать исследуемому процессу с максимальной фиксацией всех факторов. В журнале отмечают тему НИР и тему эксперимента, фамилию исполнителя, время и место проведения эксперимента, характеристику окружающей среды, данные об объекте эксперимента и средствах измерения, результаты наблюдений, а также другие данные для оценки получаемых результатов.

Журнал нужно заполнять аккуратно, без каких-либо исправлений. При получении в одном статистическом ряду результатов, резко отличающихся от соседних измерений, исполнитель должен записать все данные без искажений и указать обстоятельства, сопутствующие указанному измерению. Это позволит установить причины искажений и квалифицировать измерения как соответствующие реальному ходу процесса или как грубый промах.

Одновременно с измерениями исполнитель должен проводить предварительную обработку результатов и их анализ. Здесь особо должны проявляться его творческие способности. Такой анализ позволяет контролировать исследуемый процесс, корректировать эксперимент, улучшать методику и повышать эффективность эксперимента.

Важны при этом консультации с коллегами по работе и особенно с научным руководителем. В процессе эксперимента необходимо соблюдать требования инструкций по промсанитарии, технике безопасности, пожарной профилактике. Исполнитель должен уметь организовать рабочее место, руководствуясь принципами НОТ.

Вначале результаты измерений сводят в таблицы по варьирующим характеристикам для различных изучаемых вопросов. Очень тщательно уточняют сомнительные цифры. Устанавливают точность обработки опытных данных.

Особое место отведено анализу эксперимента – завершающей части, на основе которой делают вывод о подтверждении гипотезы научного исследования. Анализ эксперимента – это творческая часть исследования. Иногда за цифрами трудно четко представить физическую сущность процесса. Поэтому требуется особо тщательное сопоставление фактов, причин, обусловливающих ход того или иного процесса и установление адекватности гипотезы и эксперимента.

При обработке результатов измерений и наблюдений широко используют методы графического изображения. Графическое изображение дает наиболее наглядное представление о результатах экспериментов, позволяет лучше понять физическую сущность исследуемого процесса, выявить общий характер функциональной зависимости изучаемых переменных величин, установить наличие максимума или минимума функции.

Для графического изображения результатов измерений (наблюдений), как правило, применяют систему прямоугольных координат. Прежде чем строить график, необходимо знать ход (течение) исследуемого явления. Качественные закономерности и форма графика экспериментатору ориентировочно известны из теоретических исследований.

Точки на графике необходимо соединять плановой линией так, чтобы они по возможности ближе проходили ко всем экспериментальным точкам. Если соединить точки прямыми отрезками, то получим ломаную кривую. Она характеризует изменение функции по данным эксперимента. Обычно функции имеют плавный характер. Поэтому при графическом изображении результатов измерений следует проводить между точками плавные кривые.

Резкое искривление графика объясняется погрешностями измерений.

При графическом изображении результатов экспериментов большую роль играет выбор системы координат или координатной сетки.

Координатные сетки бывают равномерными и неравномерными. У равномерных координатных сеток ординаты и абсциссы имеют равномерную шкалу. Например, в системе прямоугольных координат длина откладываемых единичных отрезков на обеих осях одинаковая.

Из неравномерных координатных сеток наиболее распространены полулогарифмические, логарифмические, вероятностные.

Полулогарифмическая сетка имеет равномерную ординату и логарифмическую абсциссу.

Логарифмическая координатная сетка имеет обе оси логарифмические; вероятностная – ординату, обычно равномерную, и абсциссу – вероятностную шкалу.

Назначение неравномерных сеток разное. Чаще их применяют для более наглядного изображения функций. Так, многие криволинейные функции спрямляют на логарифмических сетках. Вероятностная сетка применяется в различных случаях: при обработке измерений для оценки их точности, при определении расчетных характеристик.

Большое значение имеет выбор масштаба графика, что связано с размерами чертежа и соответственно с точностью снимаемых, с него значений величин. Известно, что чем крупнее масштаб, тем выше точность снимаемых значений. Однако, как правило, графики не превышают размеров 20x15 см, что является удобным при составлении отчетов.

Масштаб по координатным осям обычно применяют разный. От его выбора зависит форма графика – он может быть плоским (узким) или вытянутым (широким) вдоль оси.

Расчетные графики, имеющие максимум (минимум) функции или какой-либо сложный вид, особо тщательно необходимо вычерчивать в зонах изгиба. На таких участках количество точек для вычерчивания графика должно быть значительно больше, чем на главных участках.

В некоторых случаях строят номограммы, существенно облегчающие применение для систематических расчетов сложных теоретических или эмпирических формул в определенных пределах измерения величин. Номограммированы могут быть любые алгебраические выражения. В результате сложные математические выражения можно решать сравнительно просто графическими методами. Построение номограмм – трудоемкая операция. Однако, будучи раз построенной, номограмма может быть использована для нахождения любой из переменных, входящих в номограммированные уравнения. Применение ЭВМ существенно снижает трудоемкость номо-граммирования.

Существует несколько методов построения номограмм. Для этого применяют равномерные или неравномерные координатные сетки. В системе прямоугольных координат функции в большинстве случаев на номограммах имеют криволинейную форму. Это увеличивает трудоемкость, поскольку требуется большое количество точек для нанесения одной кривой. В логарифмических координатных сетках функции имеют прямоугольную форму и составление номограмм упрощается.

В процессе экспериментальных измерений получают статистический ряд измерений двух величин объединяемых функций: У = F(X).

Каждому значению функции у_г,..., у_п соответствует определенное значение аргумента х_г, х₂,..., х_п.

На основе экспериментальных данных можно подобрать алгебраические выражения, которые называют эмпирическими формулами. Такие формулы подбирают лишь в пределах измеренных значений аргумента х₁ - х_п. Эмпирические формулы имеют тем большую ценность, чем больше они соответствуют результатам эксперимента.

Необходимость в подборе эмпирических формул возникает во многих случаях. Так, если аналитическое выражение У = F(X) сложное, требует громоздких вычислений, составления программ для ЭВМ, то часто эффективнее пользоваться упрощенной приближенной эмпирической формулой. Опыт показывает, что эмпирические формулы бывают незаменимы для анализа измеренных величин. К эмпирическим формулам предъявляют два основных требования – по возможности они должны быть наиболее простыми и точно соответствовать экспериментальным данным в пределах изменения аргумента.

Таким образом, эмпирические формулы являются приближенными выражениями аналитических. Замену точных аналитических выражений приближенными, более простыми, называют аппроксимацией, а функции – аппроксимирующими.

Процесс подбора эмпирических формул состоит из двух этапов. На первом этапе данные измерений наносят на сетку прямоугольных координат, соединяют экспериментальные точки плавной кривой и выбирают ориентировочно вид формулы. На втором этапе вычисляют параметры формул, которые наилучшим образом соответствовали бы принятой формуле. Подбор эмпирических формул необходимо начинать с самых простых выражений.

Кривые, построенные по экспериментальным точкам, выравнивают известными в статистике методами. Например, методом выравнивания, который заключается в том, что кривую, построенную по экспериментальным точкам, представляют линейной функцией. Для нахождения параметров заданных уравнений часто применяют метод средних и метод наименьших квадратов.

Для исследования закономерностей между явлениями (процессами), которые зависят от многих, иногда неизвестных факторов, применяют корреляционный анализ.

В процессе проведения эксперимента возникает потребность проверить соответствие экспериментальных данных теоретическим предпосылкам, т. е. проверить гипотезу исследования. Проверка экспериментальных данных на адекватность необходима также во всех случаях на стадии анализа теоретико-экспериментальных исследований. Методы оценки адекватности основаны на использовании доверительных интервалов, позволяющих с заданной доверительной вероятностью определять искомые значения оцениваемого параметра. Суть такой проверки состоит в сопоставлении полученной или предполагаемой теоретической функции У = F(X) срезультатами измерений.

В практике адекватности применяют различные критерии согласия: Фишера, Пирсона, Романовского.

Выбор и составление плана эксперимента

Наиболее часто при выполнении НИР целью экспериментальных исследований является получение математической модели объекта, т.е. математической зависимости j свойства изучаемого объекта (условно обозначим его y) от значений факторов (x _j), влияющих на эти свойства: y = j(x ₁, x ₂,..., x _j,... x _k) + e, где e - величина, не зависящая от x _j (назовем ее случайной величиной).

Выбор плана эксперимента зависит от того, какой характер зависимости j вы желаете получить: качественный или количественный. Зависимость j является качественной, если она выражается словами, например: " x _j влияет на y ", " увеличение x _j уменьшает значение y " и др. Зависимость j является количественной, если она представляет собой уравнение или систему уравнений.

Так как результаты измерений значений x _j и y являются случайными величинами, то для установления зависимости j необходимо использовать соответствующие методы математической статистики.

Для получения качественной зависимости j наиболее часто используют методы корреляционного и дисперсионного анализов, для получения количественной зависимости - метод регрессионного анализа. Производными от этих методов являются другие методы: ковариационного, кластерного, факторного анализов и др.

Планирование эксперимента для применения корреляционного анализа. Корреляционный анализ - это один из наиболее простых методов математической статистики, позволяющий качественно предсказывать изменения y при изменяющихся значениях xj (устанавливать связь между этими случайными величинами).

Если каждому значению x _j соответствует всегда строго определенное значение y, то считают, что между этими величинами существует функциональная связь, т.е. зависимость j является функциональной. При наличии и знании такой зависимости можно точно предсказывать величину y, задавая конкретное значение x _j.

Однако на практике функциональные зависимости обнаруживаются очень редко, поскольку на все результаты измерений оказывают влияние различные случайные факторы.

В большинстве случаев, задавая конкретное значение x _j, можно предсказать лишь тенденцию изменения y. Эта тенденция обнаруживается лишь при достаточно большом числе m_j различных значений (уровней) изменяемого фактора x _j, а при малых величинах m_j данная тенденция может не наблюдаться (рисунок 1.6).

Рис. 1.6 – Влияние числа значений х (m) на тенденцию изменения y: 1 - тенденция изменения y при m = 8, 2 - тенденция изменения y при m = 3

Связь между y и x, представленная на рисунке 1, называется корреляционной (стохастической). Чем больше корреляционная связь соответствует функциональной связи, тем более тесной она считается.

Корреляционная связь имеет два крайних предельных случая: функциональная связь (самая тесная зависимость y от x _j) и полное отсутствие связи (влияния x _j на y).

Наличие между y и x _j корреляционной или функциональной связи устанавливается только в результате проведения корреляционного анализа.

При корреляционном анализе отражают следующие выводы в форме слов:

Наличие зависимости между y и x _j ("есть" или "нет" и др.)

Характер зависимости ("функциональная" или "корреляцион­ная") и ее тип ("линейная", "нелинейная", "экспоненциальная", "пара­болическая", "синусоидальная" и др.)

Знак связи: "положительная" - если с увеличением величины значений x _j растет величина y; "отрицательная" - если с уменьшением величины значений x _j снижается величина y.

Теснота (сила) корреляционной связи ("очень тесная", "тесная", "не очень тесная", "ярко выраженная", "выраженная", "слабо выраженная" и др.)

Корреляционный анализ проводят двумя методами: анализом поля корреляции и анализом коэффициента линейной корреляции [42, 43].

Составление планов эксперимента с учетом возможности проведения корреляционного анализа.

Корреляционный анализ не накладывает повышенных требований к планированию эксперимента. Единственным обязательным условием является выполнение соотношения m_j > 2. Из рекомендаций по планированию эксперимента для проведения корреляционного анализа можно привести следующие. Желательно, чтобы план эксперимента предусматривал:

1) широкую область изменения значений факторов x _j;

2) большое число m_j значений (уровней) факторов x _j, при этом разница между уровнями должна быть больше абсолютной погрешности их измерения;

3) повторные опыты для каждого значения факторов x _j;

4) большое общее число измерений (N).

Планирование эксперимента для применения дисперсионного анализа.Дисперсионный анализ - это метод математической статистики, который широко применяется в различных отраслях науки как самостоятельно, так и в сочетании с другими методами.

Суть дисперсионного анализа заключается в сравнении между собой двух или более дисперсий и доказательстве нуль-гипотезы разности этих дисперсий.

При установлении зависимости j дисперсионным анализом исходят из следующих соображений.

В эксперименте изменения средних арифметических значений свойства объекта (` y <sub>v</sub>) зависят не только от изменяемых факторов x <sub>j</sub> (с известными уровнями), но и от случайных факторов. Поэтому рассеивание (разброс)` y _v относительно общего среднего арифметического значения (рисунок 1.7), характеризуемое общей дисперсией (), разделяется на составляющие: рассеивание, обусловленное случайными факторами (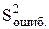, , ), и рассеивание, обусловленное известными факторами за счет изменения их значений, т.е. перехода с одного уровня на другие (, и др.). Попарное сравнение всех факторных дисперсий () с дисперсией, характеризующей действие случайных факторов, т.е. воспроизводимость эксперимента (), позволяет на основании закона распределения Фишера сделать следующие основные выводы дисперсионного анализа:

Установить или опровергнуть влияние x _j на y с заданной вероятностью ("влияет", "не влияет" и др.).

Определить вероятность влияния x _j на y.

Рис. 1.7 - Поле корреляции величин y и x

Так, например, после проведения эксперимента и математической обработки результатов измерений можно вычислить F-отношение (F_p):

; ; .

Задав вероятность (Р) и вычислив по известным формулам числа степеней свободы для факторной дисперсии f_факт. (f₁) и дисперсии воспроизводимости f_воспр. (f₂), из справочных данных выбираем табличное значение квантиля распределения Фишера (F_т). При выполнении неравенства F_P> F_т можно делать вывод, что данный фактор х с вероятностью Р влияет на свойство y, т.е. "значима" разность между влиянием на свойство y известного фактора х и случайных факторов. При невыполнении этого неравенства делается вывод об отсутствии влияния фактора х на свойство y, т.е. это влияние соизмеримо со случайными ошибками эксперимента.

Дисперсионный анализ по сравнению с корреляционным анализом имеет существенные преимущества:

1. Позволяет делать однозначные и более точные выводы о влиянии фактора x _j на свойство y.

2. Позволяет определить влияние на свойство y не только количественных, но и качественных факторов (например, типа растворителя, времени года и др.).

3. Позволяет оценить значение (уровень) фактора x _j, при котором он начинает влиять с заданной вероятностью на свойство y.

Планирование эксперимента для проведения дисперсионного анализа зависит от числа известных факторов, одновременно изменяемых в эксперименте. Различают планы экспериментов для проведения одно-, двух- и многофакторного (трех- и более) дисперсионного анализа.

Составление планов эксперимента для проведения дисперсионного анализа.

Общим требованием к планированию любого эксперимента для проведения дисперсионного анализа является выполнение условия
m_j > 1. Желательно, чтобы план эксперимента для проведения дисперсионного анализа предусматривал:

1) широкую область изменения значений факторов x _j,

2) большое число m_j значений (уровней) факторов x _j, при этом разница между уровнями должна быть больше абсолютной погрешности их измерения.

Остальные требования к составлению плана эксперимента зависят от числа исследуемых факторов и выбранного числа опытов.

Составление планов экспериментов для проведения однофакторного дисперсионного анализа.

Введем следующие обозначения:

Тогда при одинаковом числе повторений опытов для каждого уровня фактора А:

N = mn.

Классической формой плана для проведения однофакторного дисперсионного анализа является таблица (табл. 1.1). Условные обозначения уровней фактора часто называют "кодированными" значениями фактора, а реальные значения (качественные или количественные) - натуральными значениями.

Таблица 1.1

План эксперимента для проведения однофакторного дисперсионного анализа с кодированными значениями уровней фактора А

Очевидно, что число пустых клеточек в табл. 8 соответствует общему числу опытов в эксперименте (N). В эти клеточки после проведения соответствующего опыта заносят измеренное значение свойства объекта y.

Составление планов экспериментов для проведения двухфакторного дисперсионного анализа.

Двухфакторный дисперсионный анализ предусматривает возможность проведения экспериментов без повторения опытов. Если обозначить второй фактор В, максимальное число его уровней w и номер уровня q, то общее число опытов в плане эксперимента без повторения опытов будет равно:

N = mw.

Классический план такого эксперимента (табл. 1.2) является планом полного факторного эксперимента (ПФЭ), так как в нем предусмотрены опыты со всеми возможными сочетаниями различных уровней всех факторов.

Более понятным для выполнения является развернутый план эксперимента. Развернутый план получают из классического плана, присвоив в случайном порядке (принцип рандомизации) номера опытов каждой пустой ячейке табл. 1.2. Условия проведения каждого опыта (табл. 1.3) определяются исходя из того, какие столбец и строка (уровни фактора А и В) совмещаются в ячейке с данным номером опыта.

Таблица 1.2

План эксперимента для проведения двухфакторного дисперсионного анализа с кодированными значениями уровней факторов

Таблица 1.3

Развернутый план эксперимента для проведения двухфакторного дисперсионного анализа с кодированными значениями уровней факторов

Если в плане эксперимента предусмотреть повторение каждого опыта, то тогда при проведении дисперсионного анализа результатов измерений y можно оценить влияние на данное свойство объекта эффекта одновременного изменения двух факторов (эффектов "взаимодействия" факторов). Эффекты взаимодействия могут иметь синергетический (взаимоусили­вающий) или антагонистический (взаимоослабляющий) характер влияния одновременного изменения факторов x _j на свойство y.

Составление планов экспериментов для проведения многофакторного дисперсионного анализа.

При многофакторном эксперименте одновременно изменяются три и более факторов. Общее число опытов (без их повторений) для ПФЭ с k изменяемыми факторами (если каждый из них имеет одно и то же максимальное число уровней m) будет равно:

N_ПФЭ= m^k.

Очевидно, что с увеличением числа исследуемых факторов (k) общее число опытов в эксперименте будет резко возрастать. Поэтому при многофакторных экспериментах часто применяют планы дробных факторных экспериментов (ДФЭ), которые предусматривают выполнение опытов только с частью всех возможных сочетаний различных уровней всех факторов. Долю общего числа опытов ДФЭ (N_ДФЭ) от N_ПФЭ называют степенью дробности ДФЭ.

Очевидно, что с увеличением числа исследуемых факторов (k) общее число опытов в эксперименте будет резко возрастать. Поэтому при многофакторных экспериментах часто применяют планы дробных факторных экспериментов (ДФЭ), которые предусматривают выполнение опытов только с частью всех возможных сочетаний различных уровней всех факторов. Долю общего числа опытов ДФЭ (N_ДФЭ) от N_ПФЭ называют степенью дробности ДФЭ.

Необходимо помнить, что сокращение числа опытов в эксперименте, т.е. переход от ПФЭ к ДФЭ, всегда приводит к снижению точности дисперсионного анализа результатов эксперимента.

Существуют различные принципы составления и типы планов ДФЭ: составление планов по принципу дробных реплик, латинских квадратов и кубов, планы Плакетта-Бермана и др. Эти планы относятся к планам математического планирования эксперимента, так как при их построении сочетание уровней факторов в опытах (выбор части опытов из планов ПФЭ) происходит не произвольно, а по определенным принципам математической комбинаторики.

Планы ДФЭ широко применяются при отсеивающих экспериментах, т.е. тогда, когда необходимо изучить достаточно большое число факторов при небольшом числе опытов и определить те факторы, которые оказывают наиболее сильное влияние на свойство y. Одними из самых экономичных по числу опытов и эффективных для дисперсионного анализа из известных планов ДФЭ являются планы Плакетта-Бермана.

Правильность построения плана Плакетта-Бермана определяется двумя признаками:

1. Диагональным расположением одинаковых знаков в ячейках плана.

2. Равенством количества знаков (+) и (-) в каждом столбце плана.

План с натуральными значениями факторов получается из плана с кодированными значениями путем замены знаков (+) и (-) на соответствующие им натуральные значения для каждого фактора.

Примеры составления других планов многофакторного ДФЭ для проведения дисперсионного анализа и алгоритмы математической обработки результатов эксперимента изучите самостоятельно [8].

Проведение дисперсионного анализа можно легко осуществить с помощью ПЭВМ с использованием различных общепризнанных статистических программных продуктов: STATGRAPHICS, STADIA [7], STATISTICA и др.

Планирование эксперимента для применения регрессионного анализа. Регрессионный анализ (РА) - метод математической статистики, который позволяет выявить приближенную количественную зависимость (f) свойства объекта y от значений факторов x_j, оказывающих влияние на это свойство. Эта приближенная зависимость, выраженная в виде конкретной математической функции, называется уравнением регрессии:

.

Проводить РА можно только для количественных значений y и x _j.

При РА решают две основные задачи:

1. Ищут с помощью метода приближения уравнение регрессии, наиболее точно описывающее истинную зависимость y = j(x _j) по результатам измерения свойств объекта при различных значениях факторов:

y = j(x ₁, x ₂,..., x _j,... x _k) + e = f(x ₁, x ₂,..., x _j,... x _k) + q + e.

2. Оценивают ошибки (q + e), допускаемые при описании истинной зависимости j с помощью найденного уравнения регрессии.

Порядок проведения РА (его тип) зависит от плана эксперимента. Различают классический РА (КРА) и РА при математическом планировании эксперимента (РАМПЭ).

Составление планов эксперимента для проведения классического регрессионного анализа. Общим требованием к планированию любого эксперимента для проведения КРА является выполнение условия m_j > 2. Другие рекомендации аналогичны планированию эксперимента для проведения дисперсионного анализа.

После планирования и завершения эксперимента проведение КРА его результатов проводят в такой последовательности:

Выбирают семейство математических функций, в котором предполагается найти уравнение регрессии (семейство прямых, парабол, гипербол и др.).

Выбирают метод приближения.

Для выбранного семейства функций с помощью метода приближения рассчитывают параметры функции (коэффициенты уравнения регрессии).

Проверяют рассчитанные коэффициенты уравнения регрессии на значимость (равенство нулю).

Корректируют вид исходной функции, исключая из нее незначимые коэффициенты и другие составляющие.

Рассчитывают параметры скорректированной функции (скорректированные коэффициенты уравнения регрессии) и возвращаются к выполнению пунктов 4,5. Пункт 6 выполняют до тех пор, пока в уравнении регрессии останутся только значимые коэффициенты (значения коэффициентов могут изменяться после каждого пересчета)

Оценивают ошибки (q + e), допускаемые при описании истинной зависимости j с помощью найденного уравнения регрессии: проверяют адекватность уравнения регрессии с помощью закона распределения Фишера или рассчитывают вероятность описания зависимости j функцией f.

Выбирают другое семейство математических функций и (или) метод приближения и с ними последовательно выполняют пункты 3-7.

Из группы найденных уравнений регрессии в ряду разных семейств функций выбирают окончательное уравнение регрессии по следующим соображениям:

а) вид данного уравнения регрессии совпадает с теоретическими законами поведения объекта;

б) данное уравнение регрессии описывает поведение объекта с наибольшей вероятностью;

в) при одной вероятности для данного уравнения регрессии наблюдается наибольшее значение соотношения факторной и остаточной дисперсий (F-соотношения).

При выборе семейства функций (пункты 1 и 8), если нет сведений или теоретических предположений о типе зависимости j, обычно действуют по принципу "от простого к сложному". При этом начинают с семейства прямых ("линейная регрессия") или трансцендентных функций, которые легко преобразуются в линейную форму ("трансцендентная регрессия").

При неадекватности найденного линейного уравнения регрессии или неудовлетворенности его точностью можно переходить к семейству полиномов с постепенным увеличением их степени (полиномы второго, третьего и др. порядков) до тех пор, пока не начнет уменьшаться F-соот­ношение. Вид функции также зависит от числа одновременно изменяемых факторов при эксперименте.

Наиболее часто при выполнении РА в качестве метода приближения используют метод наименьших квадратов (МНК). Однако применение МНК является корректным при выполнении следующих требований:

а) единичные результаты измерения свойств y должны быть независимыми случайными величинами;

б) выборочные дисперсии y _z должны быть однородными (одинаковыми).

При невыполнении этих условий используют другие методы приближения (непараметрические методы регрессии).

Алгоритмы всех необходимых при КРА расчетов (пункты 3,4,6,7) зависят от выбранного семейства функций, метода приближения, наличия повторных опытов, количества исследуемых факторов (изучить самостоятельно [42,43,44,45]). Многие из этих алгоритмов реализованы в статистических программных продуктах, математических пакетах (MathCAD и др.), электронных таблицах (E x cel и др.).

Следует отметить, что выполнение пункта 9 носит субъективный характер и для него пока еще нет общепризнанных рекомендаций.

Математическое планирование эксперимента для проведения регрессионного анализа.

В современных условиях, учитывая многогранность изучаемых явлений, острый дефицит времени, высокую стоимость эксплуатации научного оборудования, необходимо стремиться к наиболее рациональным планам проведения эксперимента.

Применение методов математического планирования эксперимента для проведения регрессионного анализа (РАМПЭ) приводит к увеличению точности получаемого уравнения регрессии, а иногда и к значительному сокращению числа опытов.

В основу методов математического планирования эксперимента для проведения РА положен принцип "черного ящика". Суть этого принципа заключается в том, что исследователь, не зная об истинных закономерностях поведения объекта, описывает его с помощью статистических математических моделей.

Образно говоря, "ударяя" по исследуемому объекту изменением входных параметров (x _j) в ходе эксперимента (рис. 1.8) и измеряя его реакцию (y _v) на эти "удары" при действии случайных факторов (w_z), можно получить статистическую математическую зависимость, пригодную для прогноза поведения объекта.

Рис. 1.8 - Схема объекта по принципу "черного ящика"

В отличие от детерминированных математических моделей объекта, построенных на основе фундаментальных законов физики, механики, химии или других, статистические математические модели получают, описывая зависимости выходных параметров (свойств, откликов) объекта от изменения входных параметров (факторов) с помощью полиномов различной степени.

Статистической математической моделью объекта является функция или набор функций, описывающих зависимость величин выходных параметров (свойств, отклика) объекта (y_v) от значений входных параметров (x _j):

y_v = j_v(x ₁, x ₂, x ₃,..., x _j,..., x _k) + e(w₁, w₂, w₃,..., w_z,...),

где e - вклад в изменение свойств объекта случайных факторов.

Наиболее часто в качестве статистической модели объекта используют приближенные уравнения регрессии:

.

Известно, что любую функцию (в том числе j и f) можно разложить в ряд Тейлора и представить в виде конкретного полинома определенной степени (конечного отрезка ряда Тейлора) вида:

…,

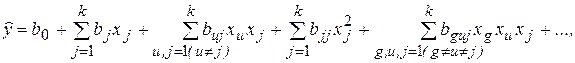
где b и b - соответственно генеральные и выборочные коэффициенты ряда Тейлора.

По результатам эксперимента возможно определить вид полинома только с выборочными коэффициентами, которые характеризуют:

b₀ - величину y при нулевом значении всех факторов (свободный член);

b₁, b₂,..., b_j,..., b_k - линейные эффекты влияния соответствующих факторов на величину y;

b₁₂, b₁₃,..., b_1j,...,b_1k, b₂₃, b₃₄,..., b_2j,..., b_(k-1)j, ..b_(k-1)k - парные эффекты влияния соответствующих факторов на величину y (эффекты "взаимодействия" двух соответствующих факторов);

b₁₁, b₂₂,..., b_jj,..., b_kk - квадратичные эффекты влияния соответствующих факторов на величину y;

b₁₂₃, b₁₂₄,..., b_1uj,..., b₂₃₄, b₂₃₅,..., b_2uj,..., b_(k-2)(k-1)k - тройные эффекты влияния соответствующих факторов на величину y (эффекты "взаимодействия" трех соответствующих факторов) и т.д.

Наиболее удобно планировать эксперимент математическими методами для кодированных значений факторов (x _j), получаемых из натуральных значений (X _j) по следующим формулам:

; ; ,

где - натуральное значение фактора в центре (середине) выбранной

(заданной) области изменения (варьирования) фактора, и - соответственно максимальное и минимальное значения фактора в выбранной области его изменения. В соответствии с этими формулами натуральному значению X _j = соответствует кодированное значение x _j = 0; X _j = - кодированное значение x _j = +1, а X _j = - значение x _j = -1.

Переход от кодированных значений факторов к натуральным осуществляют по формуле:

.

Выбор плана эксперимента для применения РАМПЭ в отличие от планирования экспериментов для проведения КРА определяется видом выбранного семейства функций (видом полинома).

После завершения эксперимента для проведения РАМПЭ выполняют следующие действия:

Выбирают вид полинома (отрезок ряда Тейлора) для поиска уравнения регрессии.

Для выбранного полинома с помощью МНК рассчитывают параметры функции (выборочные коэффициенты уравнения регрессии).

Проверяют рассчитанные выборочные коэффициенты уравнения регрессии на значимость (равенство нулю).

Корректируют вид исходной функции, исключая из нее незначимые коэффициенты и другие составляющие.

Оценивают ошибки, допускаемые при описании истинной зависимости j с помощью найденного уравнения регрессии: проверяют адекватность уравнения регрессии с помощью распределения Фишера или рассчитывают вероятность описания зависимости j функцией f.

Если точность найденного уравнения регрессии не удовлетворяет, то выбирают, планируют и реализуют другой план эксперимента для поиска уравнения регрессии в другом семействе полиномов (например, полиномов более высокого порядка).

Порядок проведения РАМПЭ в отличие от КРА имеет следующие особенности:

Выбирается только один класс функций - полиномы.

Используется только один метод приближения - МНК.

После корректировки уравнения регрессии его коэффициенты не пересчитываются.

Выполняется меньшее количество этапов РА.

Обычно поиск уравнения регрессии начинают в семействе самых простых полиномов: первого и второго порядка. По названиям степеней полиномов называют и планы эксперимента для применения РАМПЭ [43, 46, 47].

Планирование эксперимента для решения оптимизационных задач

Оптимизационные задачи в большинстве случаев формулируются как задачи поиска экстремальных значений функции отклика объекта (максимумов или минимумов). Например, инженеру часто приходится решать задачи поиска оптимальных условий производства продукции с максимальной производительностью или минимальной себестоимостью.

Поведение объекта во многих случаях приходится описывать несколькими функциями отклика. Очень редко удается найти такое сочетание значений всех влияющих факторов, при котором достигаются все желаемые экстремумы функций отклика объекта. Большинство влияющих факторов можно изменять только в реальных пределах: концентрации реагентов не могут быть отрицательными, температуры процессов не могут превышать безопасные значения и т.д. Исследователю нужны и реальные значения функции отклика объекта: неотрицательные значения выхода продукции, степени очистки, себестоимости продукции и др. Поэтому в большинстве случаев оптимизационные задачи решают при условии различных ограничений на величину влияющих факторов и значений функций откликов объектов, т.е. проводят поиск рациональны х значений влияющих факторов.

При традиционном поиске рациональных условий стабилизируют все факторы, кроме одного. При этом зачастую обнаруживается только часть экстремальных значений функции отклика объекта («локальные» экстремумы).

Для получения более полной информации о поведении объекта рекомендуется проводить поиск рациональных условий при одновременном изменении нескольких факторов, используя специальные методы математического планирования эксперимента [43,46-49].

Все методы математического планирования эксперимента для решения оптимизационных задач делят на две группы: методы, требующие знаний уравнения регрессии функции отклика объекта, и методы, не требующие таких знаний.

К группе методов, требующих знаний уравнения регрессии функции отклика объекта, относятся:

метод крутого восхождения или наискорейшего спуска по поверхности функции отклика объекта;

метод обобщенной функции желательности и др.

К другой группе методов относится симплекс-метод, или метод симплекс-планирования эксперимента.

Коротко рассмотрим суть некоторых из этих методов.

Не нашли, что искали? Воспользуйтесь поиском: